Modelling and experimental investigation of the vibratory conveyor operating conditions

2.1. 3D-model of vibratory conveyor

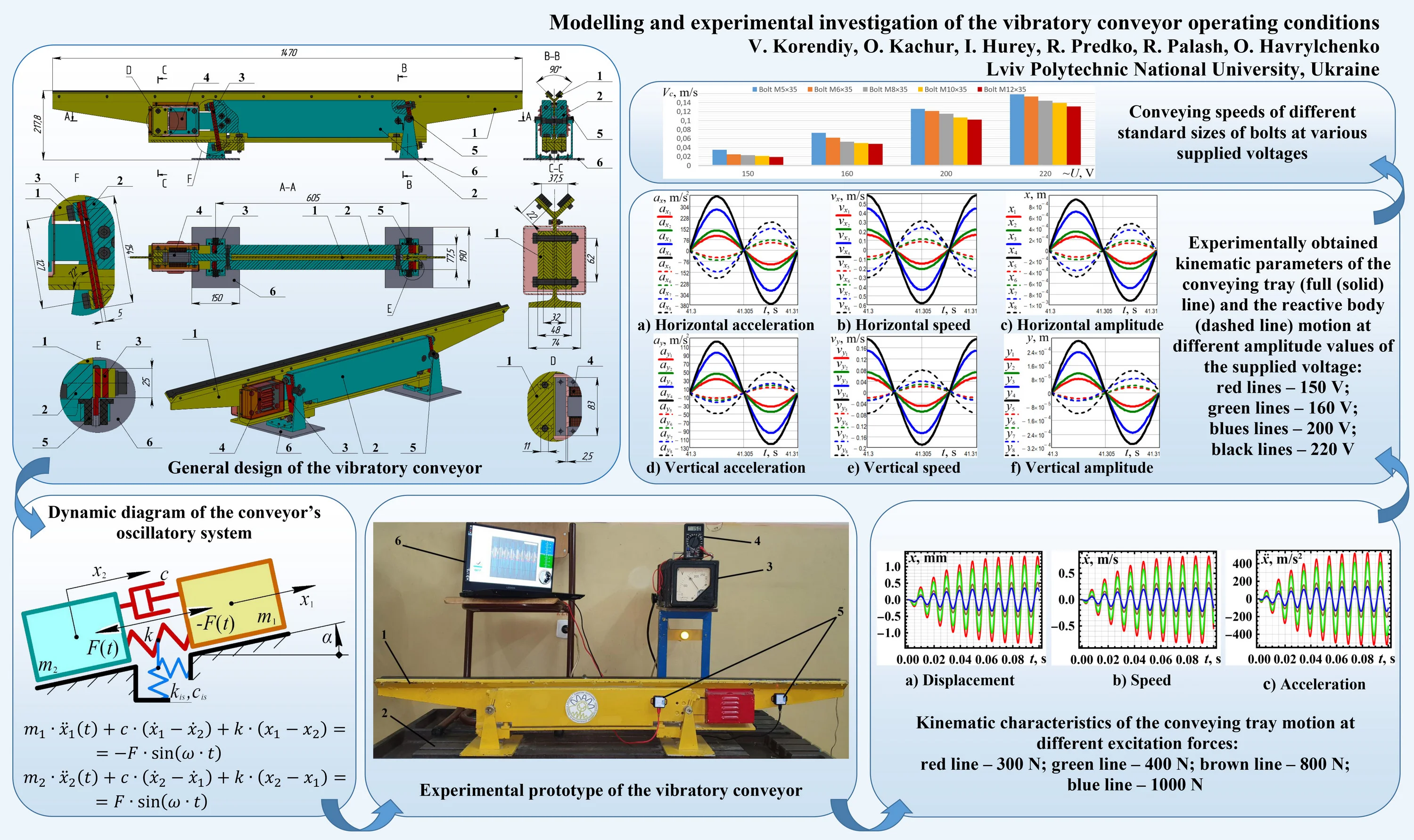
The conveyor (Fig. 1) is based on the double-mass oscillatory system characterized by the coincident mass centres of the working member 1 and the reactive body 2. This fact allows for eliminating the parasitic (angular) oscillations and providing a uniform conveying speed.

The main (central) member of the working body (conveying tray) 1 is made of the I-beam IPE160, in which the upper flange is cut off, the lower one is milled, and the additional design elements (holes, cuts, chamfers, etc.) are applied. On the lower flange, there are fixed supporting shoes to which the flat springs 3 are connected. At the rear end of the I-beam, the armature of the electromagnetic exciter 4 is installed. The conveying tray (equal angle) is welded to the upper end of the I-beam’s web. In the case of conveying the significantly larger parts, the additional strips (bars) can be attached to the angle. The reactive (non-conveying, disturbing) body 2 consists of two thick cheeks (plates), which are fixed to one another by a set of bolts freely passing through the corresponding holes drilled in the I-beam’s web. Four sets of flat springs 3 are connected to the bevelled end faces of the cheeks. In order to improve the springs fixation (restraint), additional metal sleeves (spacers) are installed between the springs at the corresponding fixation positions. At the rear end of the reactive body 2, the pull-type (single-cycle) electromagnet 4 with the frame-type coil is installed. The conveyor is mounted on the stationary base (foundation) 6 with the help of the arms (brackets) extending from the flat springs 3 and supported by the rubber vibration isolators 5. The positions of the arms correspond to the springs’ “zero-motion” points, which are almost unmovable due to the antiphase oscillations of the working member 1 and the reactive body 2. This allows for reducing the negative influence of the conveyor’s vibrations upon the stationary base (foundation) 6.

The vibratory conveyor is driven by the electromagnet 4 powered by a controllable voltage (within the range of 0…220 V) at the forced frequency of 100 Hz. The periodic electromagnetic pulling force acting between the armature (attached to the working member 1) and the core (fixed on the reactive body 2) excites the antiphase oscillations of the conveyor’s elements. Due to applying the inclined flat springs 3 connecting the vibrating bodies, the rectilinear oscillations of the working member (conveying tray) are generated at a specific angle to the horizon. This allows for conveying various piecewise products along the tray at different operating conditions (detachable (bouncing, hopping, jumping over the conveying surface) and non-detachable (sliding along the conveying surface)) depending on the kinematic characteristics (horizontal and vertical accelerations and speeds) of the tray.

Fig. 1General design of the vibratory conveyor

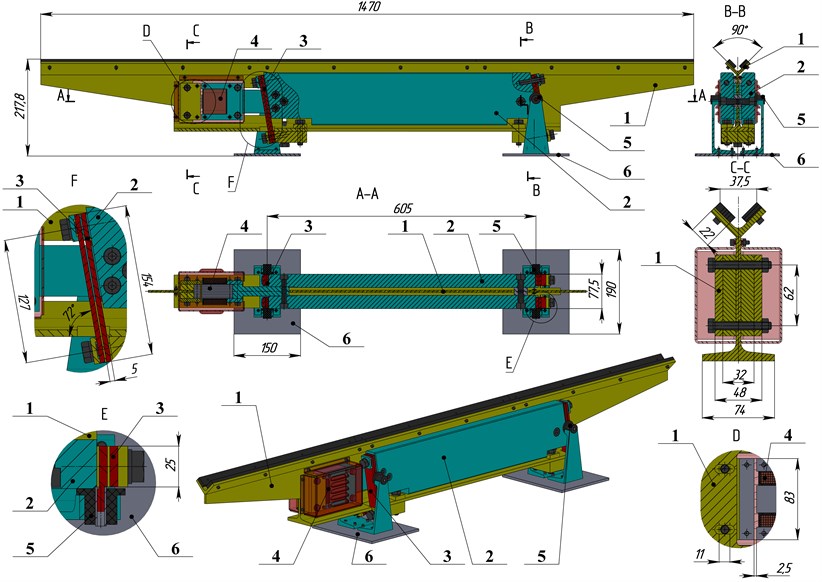
2.2. Dynamic diagram and mathematical model of the conveyor’s oscillatory system

Based on the developed design of the vibratory conveyor presented above, let us construct the dynamic diagram of its oscillatory system (Fig. 2). The latter consists of two solid bodies (of masses $m_1$ and $m_2$) connected with one another by a spring of stiffness $k$. The value of $k$ is calculated as $k=\left(m_1\bullet m_2\right)/\left(m_1+m_2\right)\bullet {\left(\omega /z\right)}^2$ to provide the conveyor operation under the efficient near-resonance conditions with the regulation coefficient $z$ (0.94…0.98). The vibrations are excited by the periodic force of the amplitude value $F$ at the forced frequency $\omega$. The energy losses in the oscillatory system are described by the damping coefficient $c$. Due to the specific design of the conveyor’s flat springs, the system vibrations are not transmitted to the base (foundation). That’s why the vibration isolators characterized by the stiffness ($k_{is}$) and damping ($c_{is}$) coefficients are not considered in the simplified mathematical model:

2.3. Experimental technique and equipment

The experimental prototype of the vibratory conveyor (Fig. 3) has been manufactured and tested at the Vibroengineering Laboratory of Lviv Polytechnic National University. The conveyor 1 is mounted on the horizontal base 2. The electromagnetic exciter is powered by the adjustable-ratio autotransformer (moving-coil voltage regulator) 3, whose voltage is additionally monitored by the voltmeter 4. The control system is connected to a single-phase power supply socket of alternating voltage (220 V). The accelerometers 5 (WitMotion BWT901CL sensors) are fixed on the working member (conveying tray) and the reactive (disturbing) body. The experimental data is sent to the laptop 6 and processed with the help of the WitMotion software.

Fig. 2Dynamic diagram of the conveyor’s oscillatory system

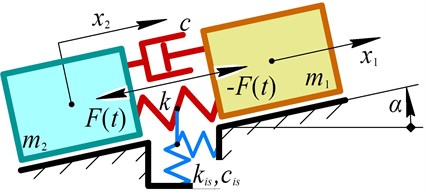
Fig. 3Experimental prototype of the vibratory conveyor

3.1. Numerical modelling of the conveyor vibrations in the Mathematica software

Based on the 3D-design and experimental prototype of the vibratory conveyor, the following inertial parameters are obtained: $m_1=$ 17.2 kg, $m_2=$ 34.2 kg. The stiffness coefficient of the flat springs set ($k=$4.9·10⁶ N/m) is calculated to provide the conveyor near-resonance operation at the forced frequency $\omega =$100 Hz. The damping coefficient ($c=$600 N·s/m) is applied on the basis of previous authors’ investigations published in [15] and [16]. The amplitude values $F$ of the excitation force (300 N, 400 N, 800 N, 1 kN) have been experimentally measured in accordance with the voltages supplied to the electromagnetic exciter (150 V, 160 V, 200 V, 220 V). The results of numerical modelling carried out in the Mathematica software are presented in Fig. 4. The results show that the maximal displacement, speed, and acceleration of about 1.3 mm, 0.8 m/s, and 500 m/s², respectively, are reached at the excitation force of the 1 kN magnitude.

Fig. 4Kinematic characteristics of the conveying tray motion at different excitation forces: red line – 300 N; green line – 400 N; brown line – 800 N; blue line – 1000 N

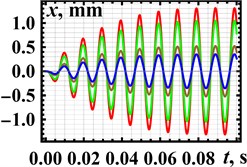
a) Displacement

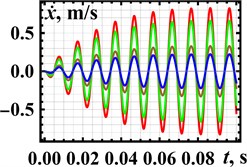
b) Speed

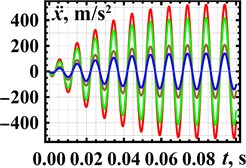
c) Acceleration

3.2. Results of experimental investigations

The experimental investigations have been conducted at different values of the supplied voltage $U$ (150 V, 160 V, 200 V, 220 V). The data obtained from the accelerometers has been processed in the WitMotion and MathCad software. The results of experiments are presented in Fig. 5 separately for horizontal and vertical directions of the conveying tray and reactive body motions. The maximal horizontal displacement, speed, and acceleration of the conveying tray (black solid lines in Fig. 5(a-c)) equal about 0.93 mm, 0.59 m/s, and 370 m/s², respectively, and are reached at the supplied voltage of 220 V. The maximal values of the corresponding vertical kinematic parameters are about 0.3 mm, 0.19 m/s, and 120 m/s², respectively (see Fig. 5(d-f)).

Fig. 5Experimentally obtained kinematic parameters of the conveying tray (full (solid) line) and the reactive body (dashed line) motion at different amplitude values of the supplied voltage: red lines – 150 V; green lines – 160 V; blues lines – 200 V; black lines – 220 V

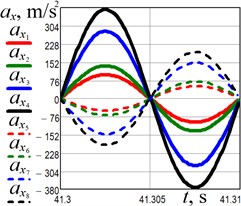
a) Horizontal acceleration

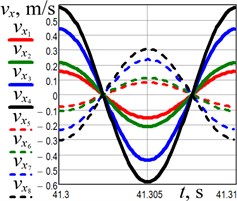
b) Horizontal speed

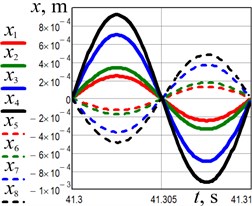
c) Horizontal displacement

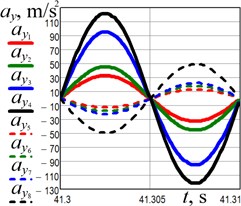
d) Vertical acceleration

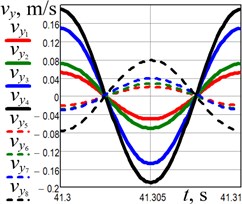
e) Vertical speed

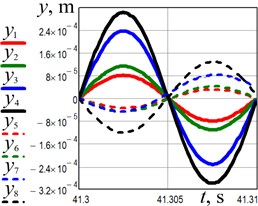
f) Vertical displacement

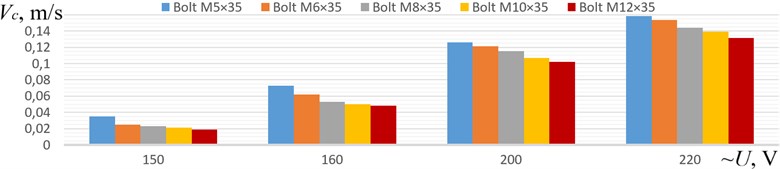
The last stage of experimental investigations is dedicated to studying the influence of the supplied voltage $U$ on the conveying speed $V_c$ of different standard sizes of bolts (ISO 4014): M5×35, M6×35, M8×35, M10×35, M12×35 (see Fig. 6). The largest conveying speed of about 0.16 m/s has been reached for the bolt M5×35 at the supplied voltage of 220 V. At the same excitation conditions, the largest bolt M12×35 moves at a speed of about 0.13 m/s.

Fig. 6Conveying speeds of different standard sizes of bolts at various supplied voltages