Experimental vibration test of the cycloidal gearbox with different working conditions

1. Introduction

The cycloidal gearboxes are mainly used in the heavy machines because of their overload capability and large reduction ratio in one stage. The biggest advantages of the cycloidal gears are a small backlash, a large reduction ratio and a high accuracy. Because of these features, they are increasingly used in robotics, especially in positioners and multi-axis robots in the first joints, where stiffness is more desirable than a small mass.

Big reduction ratio connected with the relatively high velocities on the gear output requires large input speed which causes a problem with the vibration, additionally the general principle of the gear work impose vibration problems. Despite this, the literature is rather poor in articles dedicated to cycloidal gearbox vibrations.

In the literature, some research can be found, including studies dedicated to operational principles, the generation of the cycloid shape and analytical calculations of the gear with geometrical relations [1-3]. The empirical equation relating to machining tolerance with backlash and effective torque ripple was presented in [4] and a mathematical model that includes kinematics parameters and machining step to output moment calculations compared with experimental data was studied in [5]. Propositions of a cycloid generation with the elimination of lobes undercutting was proposed at [6-11]. There is also some work dedicated to the power loss and efficiency calculation [12-14]. The article [15] tries to give a unified approach to the designer how to optimize any cycloidal gear in comparison to other gear transmissions. The research [16] presents a comparison of the one stage gears – cycloidal and harmonic – in robotics.

2. Model

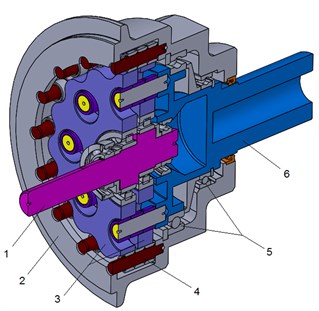
The tests were performed on the cycloidal gearbox (Fig. 1) calculated, designed and assembled at the University of Technology and Humanities in Radom.

The input shaft (1) is mounted eccentrically to cylindrical roller bearings, causing the cycloidal disc (3) to move in a circle. The cycloidal disc (3) independently rotates around the bearing as it is pushed against the housing. This is similar to planetary gearboxes and the direction of rotation is opposite to that of the input shaft. The number of external pins (4) on the housing is larger than the number of pins on the cycloidal disc. This causes the cycloidal disc (3) rotates around the bearing faster than the input shaft is moving it around, giving an overall rotation in the direction opposing the rotation of the input shaft. The cycloidal disc has holes that are larger than the output roller pins mounted on the output shaft (6) that go inside them. The output pins move around in the holes to achieve steady rotation of the output shaft (6) from the wobbling movement of the cycloidal disc

The backlash of the gear was changed with the use of the two pairs of the cycloidal discs. The first pair of the disc has the external cycloid profile at the middle of the tolerance, the profile was offset from nominal one. In second pair, external profile of the cycloidal surface was at nominal dimension and it was tolerated at a minus, additionally, modification of the diameter of the holes for output pins was introduced.

Fig. 1Cycloidal gear cross-section, isometric view: 1 – input shaft, 2 –housing, 3 – two cycloidal discs, 4 – external pins, 5 – bearing, 6 – output shaft with internal pins

3. Test bench

The gear was placed on the steel plate with a set of threaded holes which allow the change the configuration of the bench – Fig. 2. The input and output motors were supported on stiff brackets as well as the cycloidal gear. The brackets ensure bench axis alignment. On the input and output of the gear, the torque meters were mounted between elastic couplings. The bench was equipped with four thermocouples. Two of them are mounted inside the gear at the bottom and at the top. Two of thermocouples are mounted via magnets and can be placed on the side of the gear or at the support and can be used to measure ambient temperature.

Fig. 2Placement of the accelerometers with the channel numbers

4. Results

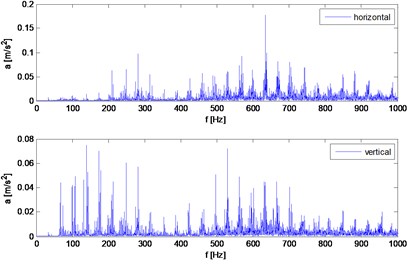
The measurements were made for the series of test with different input speed velocity (500 rpm-4500 rpm) and braking torque from no load to 42 Nm. An example of the results of the vibration measurement in the time domain (Fig. 3) and frequency domain (Fig. 4) proofs that the reduction of the clearance in the cycloidal gearbox reduces the amplitude of the vibration.

Fig. 3Comparison of vibration waveforms for small and big clearance (Red – big clearance; Black – small clearance) for 2000 rpm and 38 Nm load torque

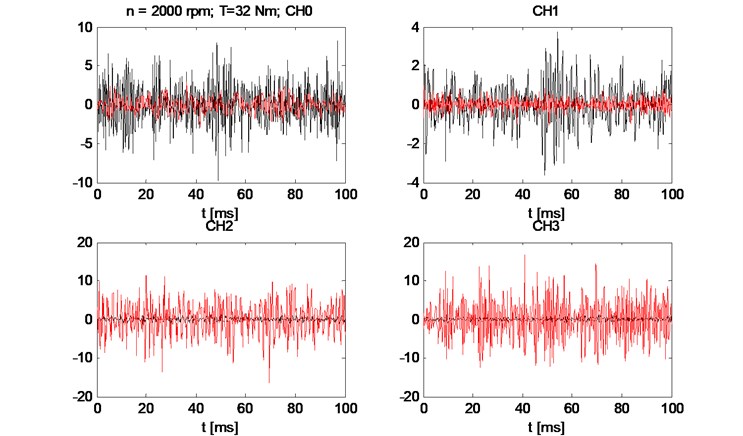
Fig. 4Spectrum of horizontal and vertical vibrations for 2000 rpm and 32 Nm load torque

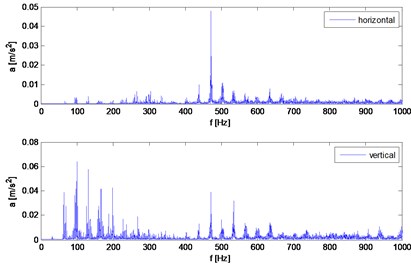
The identified mesh frequency can be calculated as:

where: $n_{inp}$ is input speed, $i=$15 is gear ratio, $n_t=$16 is number of teeth and $n_{op}=$ 8 is number of output pins.

5. Conclusions

The problem of the vibration of the cycloidal gearbox was presented in the article. The results show strong interaction between a number of external and internal pins but the external pins have biggest influence for the amplitude and for the torque fluctuation.

Additionally, an influence of the backlash to the vibration was considered. The backlash was introduced to the gear with change the cycloidal discs and the diameter of the output pin hole. The tests were performed with different load conditions.