Designing and optimizing of a novel sigma-delta modulator using PSO algorithm

1. Introduction

Embedding a micro-machined sensing element in a closed loop system is a technique, which is commonly used to achieve high performance MEMS (micro-electro-mechanical systems) sensors due to the many advantages attainable in terms of better linearity, increased dynamic range and bandwidth, and reduced parameter sensitivity to fabrication tolerances. MEMS sensors employing a capacitive sensing element incorporated in Sigma-Delta modulator control systems with electrostatic feedback have gained popularity in the past. The structure of Sigma-Delta modulator composes of the mechanical sensitivity unit and the post-stage detection circuit in the MEMS sensor system, which is able to directly convert acceleration to a digital signal and avoid the potential electro-static instability. The feedback structure of Sigma-Delta modulator effectively suppresses the quantization noise in low frequency region and emphasizes the high frequency quantization noise which can be simply removed by low pass filter. In recent years, in order to improve the performance, capacity MEMS sensor usually takes advantages of the single loop, high order Sigma-Delta modulator [1]. The designing of the high order Sigma-Delta modulator for high-performance MEMS sensor has been investigated comprehensively in [2-5]. At present, to the author’s knowledge, Sigma-Delta modulator all focused on employing additional electronic integrator in series with the mechanical sensing element to form the high order Sigma-Delta modulator [2, 3]. The stability, however, is worsen as the system order increasing, and the parameters design is much more complicated. As discussed, designing a stable and robust sensor, with high performance, is a challenging problem and is much desired to be researched.

Fractional-order calculus belongs to the branch of mathematics, which is concerned with differentiations and integrations of non-integer-order [6]. According to ref. [7], The remarkable advantage of fractional-order integrator over its counterpart integer-order one is that the stability and robustness of the fractional-order integrator is much stronger. As we all know that Sigma-Delta modulators that applied so far were all considered as integer-order modulators. Whereas, the proposed Sigma-Delta modulator with the fractional-order digital loop integrator combines some characteristics of systems between the order $N$ and ($N+1$). Therefore, we will have more possibilities for an adjustment of the poles or zeros of the noise-shaping integrator according to special requirements through changing the system order as a real (not only integer) value. In this paper, a 3rd order digital loop integrator is employed to perform noise-shaping of quantization noise from the 1-bit comparator to improve $SNR$, and furthermore a $P{I}^{\lambda }{D}^{\mu }$ controller is inserted immediately afterwards to provide the weak or strong fractional-type poles, or zeros to improve the robust stability for the proposed fractional-order Sigma-Delta modulator. The parameters of the proposed 3rd order digital loop integrator and the $P{I}^{\lambda }{D}^{\mu }$ controller are optimized by using PSO algorithm, and the optimization details will be shown in the following parts.

2. Mathematical model of the proposed fractional-order Sigma-Delta modulator

The system block diagram of the proposed fractional-order Sigma-Delta modulator is shown in Fig. 1.

Fig. 1Block diagram of the proposed Sigma-Delta modulator system

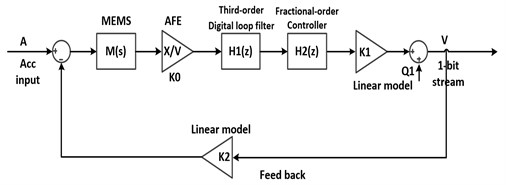
The loop is consisted of an electromechanical sensing element, a charge amplifier, a digital loop filter, a fractional-order $P{I}^{\lambda }{D}^{\mu }$ controller and a 1-bit quantizer. In Fig. 1, $k_0$ is the gain of the charge amplifier, $H_1\left(z\right)$ is the digital loop integrator, $H_2\left(z\right)$ is the fractional-order controller, $k_1$ is the 1-bit quantizer gain, $Q_1$ is the quantization noise of 1-bit quantizer, and $k_2$ is the equivalent linear model of 1-bit DAC feedback. The sensing element can be modeled as a mass-spring-damper system, a 2nd order dynamics with transfer function $M\left(s\right)$ that can be expressed as Eq. (1):

where $m$ is the proof mass, $b$ is the damping coefficient and $k$ is the spring constant.

In Fig. 1, $H_1\left(z\right)$ is the 3rd order digital loop integrator which is expressed as:

where $a_3$, $a_2$, $a_1$, $a_0$, $b_3$, $b_2$, $b_1$, $b_0$ are the coefficients of $H_1\left(z\right)$. $H_2\left(z\right)$ is the $P{I}^{\lambda }{D}^{\mu }$ controller, the transfer function of the $P{I}^{\lambda }{D}^{\mu }$ controller is expressed as:

where $\lambda$, $\mu$ are the integral order, differential order of the $P{I}^{\lambda }{D}^{\mu }$ controller, respectively.

To achieve high SNR and robust stability of the overall system, $a_3$, $a_2$, $a_1$, $a_0$, $b_3$, $b_2$, $b_1$, $b_0$ in Eq. (2) and $K_p$, $K_i$, $K_d$ in Eq. (3) are sensitively optimized by using PSO algorithm, respectively.

3. Stability analysis for fractional-order Sigma-Delta modulator system

In this paper, the proposed fractional-order Sigma-Delta modulator is described as a FO-LTI (fractional-order linear time invariant) system which generally expressed as the following form:

where $a_k\mathrm{}(k=0,\cdot \cdot \cdot n)$, $b_k\mathrm{}(k=0\cdot \cdot \cdot m)$are constants, $\alpha$ is the fractional commensurate order and $\alpha <1$. Eq. (4) can be rewritten as:

As shown in ref [8], when matrix $A$ is deterministic without uncertainty, the stability condition for Eq. (5) is clearly expressed by $\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\left|\mathrm{a}\mathrm{r}\mathrm{g}\left({\lambda }_i\right(A)\right|>\alpha \pi /2$, $i=\mathrm{1,2},\dots ,N$. In this paper, $\lambda$, $\mu$ are both set as 0.5 to inspect the effects of the half-order integrator. When $\lambda =\mu =\text{0.5}$, the fractional commensurate order of the proposed fractional-order Sigma-Delta modulator is $\alpha =\text{0.5}$. Therefore, the stability domain of the proposed fractional-order Sigma-Delta modulator is $\left|\mathrm{a}\mathrm{r}\mathrm{g}\left({\lambda }_i\right(A)\right|>\pi /4$, $i=\mathrm{1,2},\dots ,N$ as shown in Fig. 2.

Fig. 2Stable domain of the proposed fractional–order Sigma-Delta modulator

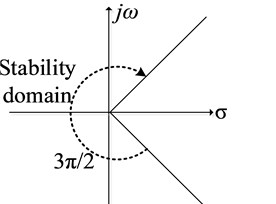
It can be seen from Fig. 2, the stability domain of the proposed fractional-order Sigma-Delta modulator is wider than that of the traditional integer-order one which stability is only in the left-half $s$-plane. Therefore, the gain margin range of the proposed fractional-order Sigma-Delta modulator is broader.

4. PSO Algorithm for fractional-order Sigma-Delta modulator

In this paper, the Simulink model of the proposed fractional-order Sigma-Delta modulator is developed shown in Fig. 3.

Fig. 3Simulink model of fractional-order Sigma-Delta modulator

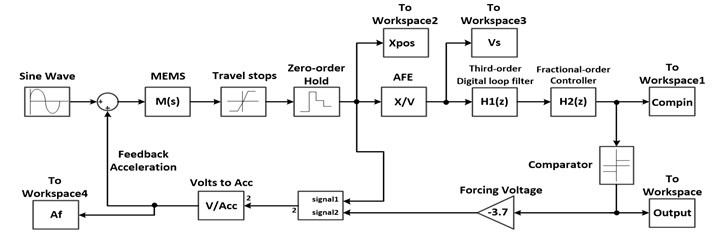
In this paper, we consider $X_i=(a_2,a_1,a_0,b_2,b_1,b_0,k_p,k_i,k_d)$ as the position vector of PSO algorithm for the proposed fractional-order Sigma-Delta modulator. The population size of the PSO algorithm is set as 40, and the individual numbers are 1000 corresponding to the dimension 9, and the iterations is 30, $\omega =\text{0.9,}{c}_1=c_2=\text{2}$. A typical objective for MEMS sensor is high $SNR$, which can be maximized and is calculated based on the power spectral density of the output bitstream. The oversampling ratio ($OSR$) needs to be specified in the proposed fractional-order Sigma-Delta modulator system. Here, we choose sample frequency is 128 kHz, and $OSR=$64.

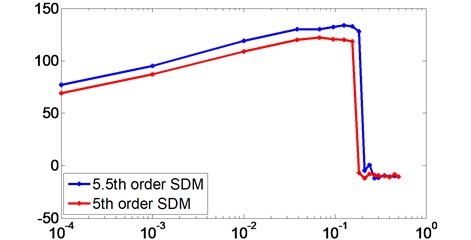
The best $X_i$ is obtained by running the PSO algorithm, and the proposed fractional-order Sigma-Delta modulator achieved about 105 dB to 135 dB of $SNR$ by yielding the different values for $X_i$ during the optimization process. The corresponding $SNR$ of the proposed fractional-order Sigma-Delta modulator is 134.011 dB which is 10X improved comparing to only 5th order Sigma-Delta modulator. The PSD plot of the fractional-order Sigma-Delta modulator is built with selected coefficients and shown in Fig. 4. Comparing to the 5th order Sigma-Delta modulator, the proposed fractional-order Sigma-Delta modulator not only performs better $SNR$, but also the wider noise floor (Bandwidth: 110 Hz in the proposed fractional-order Sigma-Delta modulator, 102 Hz in the 5th order Sigma-Delta modulator) and the sharper slope (Amplitude gain: 71.2 dB/decade in the proposed fractional-order Sigma-Delta modulator, 60.4 dB/decade in the 5th order Sigma-Delta modulator). Fig. 5 is the plot of the measured $SNR$ versus the input signal power, the two fitted curves are extended by the test data to get the estimated DR of the proposed fractional-order and the 5th order Sigma-Delta modulator.

Fig. 4PSD of the fractional-order and the integer-order Sigma-Delta modulator

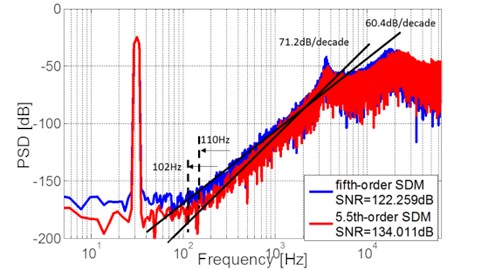
Fig. 5Measured SNR versus input signal power

5. Robust stability analysis

The root locus of the proposed fractional-order and the 5th order Sigma-Delta modulator are built and shown in Fig. 6.

In Fig. 6(b), the Root locus of the 5th order Sigma-Delta modulator pass through the right half $s$-plane, whereas, the poles and zeros of the fractional-order Sigma-Delta modulator, as shown in Fig. 6(a), are allocated along the negative axis of the $s$-plane and the farthest pole achieves –1.2×10⁷ which induce the root locus leave the right half $s$-plane. This leads to better stability of the proposed fractional-order Sigma-Delta modulator to the continuous domain frequency response.

Fig. 6Root locus comparison

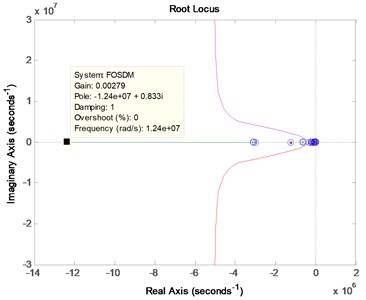
a) The proposed fractional-order Sigma-Delta modulator

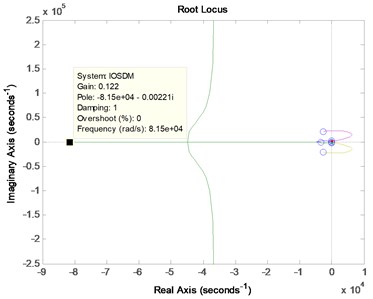
b) 5th order Sigma-Delta modulator

Similar results are also observed at system response for parametric yield errors, for instance, taking different spring constants $k_{s1}=$ 50 N/m, $k_{s2}=$ 100 N/m, $k_{s3}=$ 150 N/m in MEMS transfer function to verify the robustness of the proposed fractional-order Sigma-Delta modulator, Fig. 7 shows the PSD plot of the proposed fractional-order Sigma-Delta modulator with different spring constant $k_{s1}$, $k_{s2}$, $k_{s3}$.

Fig. 7PSD of the fractional-order Sigma-Delta modulator with different spring constant k

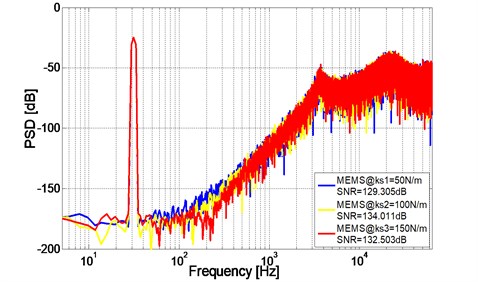
Fig. 8PSD of the proposed fractional-order Sigma-Delta modulator with different Damping coefficient b

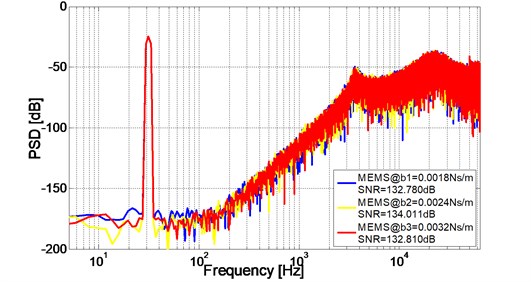
Also, taking $b_1=$ 1.8×10^-3Ns/m, $b_2=$ 2.4×10^-3Ns/m, $b_3=$ 3.2×10^-3Ns/m in MEMS transfer function, Fig. 8 shows the PSD plot of the proposed Sigma-Delta modulator with different damping coefficient $b$.

Simulation results show that $SNR$ and the Noise floor of the three sensing elements with different $k$ and three sensing elements with different $b$ only present an acceptable slight fluctuation, which indicate that the proposed fractional-order Sigma-Delta modulator also has strong robustness against to the sensitivity of MEMS devices. The response for the sensitivity of MEMS devices is very important to close the loop up in the real systematical construction.

6. Conclusions

A fractional-order Sigma-Delta modulator structure is proposed in this paper. A fractional-order $P{I}^{\lambda }{D}^{\mu }$ controller is cascaded behind the integer-order modulator to adjust the stability and SNR in fine way in Sigma-Delta modulator system. The orders of $P{I}^{\lambda }{D}^{\mu }$controller is both considered one value $\lambda =\mu =$ 0.5 as commensurate order. The proposed fractional-order Sigma-Delta modulator achieved $SNR=$134.011 dB in simulation and noise floor under –170 dB in frequency range of [5-150 Hz]. The simulated root locus shows the improved stability comparing to the pure integer-order system with good potential to progress further. This study can promote the development of high performance of MEMS sensor, also provide a scientific and technical supports for the application of fractional-order theory to practical system.