State feedback based fractional order control scheme for linear servo cart system

1. Introduction

Servomotor based linear cart system is a powerful tool for real world applications. It can reduce many men-hours through designing an automated actuating system in production lines. Basically, the servo cart system is an important key element to use in variety of processes. Depending upon the type of production plant, position and speed control of servo cart system can be of major importance. For this very purpose, several studies are performed to design position tracking and speed regulating scheme to achieve accurate tracking, robustness and increased efficiency [1]. Such as, a PI control technique is applied to improve set point tracking as described in [2]. In this investigation, a simple design is proposed to enhance the performance using dynamic weighting technique. To change the error of the process related variable, the weighting factor is produced through on-line. Feed forward, and feedback are jointly composed and proposed in a compound controller as explained in [3]. Other than the PI control technique, a fuzzy logic based PID controller is tested for servo cart position control [4]. Actually, the Fuzzy controller is implemented for a large target value. But the PID controller is applied when the values are close to the targeted value. This PID controller is tuned alone using different techniques. For instance, Luus-Jaakola Optimization technique based PID tuning process is accomplished for position and speed control of a DC servo motor [5]. Integral-Square-Error (ISE) based PID tuning is also performed for servo cart position and speed control [6]. However, this tuning was accomplished with the help of optimization technique. Servo cart position and speed controller are further designed based on sliding mode control, PD control and PI control techniques [7-10]. In fact, 90 % of industrial processes are equipped with this PID controller. Perfect parameter tuning is the main aspect of this type of control. A chaotic ant colony algorithm with the adaptive multi-strategies (CASOAMS) concept is implemented to animatedly tuning the constraints of PID controller for the purpose to justify the effectiveness of various physical systems [11]. The adaptive control idea is implemented in to genetic algorithm (GA) and colony optimization algorithm to propose an adaptive collaborative optimization technique (MGACACO) for solving complex real-world optimization problems [12].

A self-adaptive algorithm is introduced recently based on artificial bee colony (ABC) optimization technique [13]. It is claimed that the proposed ABC algorithm is better than other EAs techniques for various physical real-world problems. It is also crucial to minimize the boundary errors while controlling support vectors of some physical systems. Therefore, a v-support vector classification (ν-SVC) is proposed implementing a robust regularization path algorithm [14]. Further, the ν-SVC is modified to propose an effective incremental support vector ordinal regression (SVOR) algorithm [15, 16]. Multiple constraints based real world control problems are suitable to be handled with this algorithm while the quadratic formulations are readily available. A multi-scale local phase quantity (LPQ) and principal component analysis (PCA) is proposed to construct the feature vectors of a fingerprint liveness detection algorithm [17].

It can be mentioned that the above controllers are considered as integer order controllers in general. But currently the fractional order differentiation and integration becomes an innovative technique to implement in various branches of science and technology. Specially for the automation industry, designing a fractional order controller is an attractive tool for researchers. Therefore, it opens a wide door to re-investigate and reexamine all the former works conducted so far based on integer order calculus. It is already well known that the effectiveness of integer order controller can be enhanced with the help of fractional order differentiation and integration [18-20]. While the tuning process is concerned to obtain the most suitable gain parameter, the fractional order controllers are flexible enough in compare to that of integer order techniques. Although the parameter tuning of fractional controllers is a complex process, yet there are various effective tuning techniques introduced and published in several papers (see for example [21]).

Some other works are accomplished for modeling fractional order real-world systems using fractional-order operator. For example, an operator without a singular kernel is implemented for modelling a fractional order steady heat flow process which developed an analytical solution of dynamic equations [22, 23]. An integral transform operator is also designed and implemented on the heat-diffusion problem [24]. Another type of fractional operator with a variable order is developed using monotonic increasing function and justified the usefulness for transport process [25]. Again, non-differentiable elements based LC circuit is studied using local fractional calculus, and obtained results were compared with the relaxation oscillator (RO) circuit [26]. Besides, fractional calculus based improved adaptive particle swarm optimization(DOADAPO) algorithm is proposed to solve gate assignment problem of airport [27].

In this current investigation, the challenge is taken to design a fractional order linear controller to control the position and speed of a linear servo cart system. Now a day, the fractional order method is being used for technology transfer, but a little significant work has been done based on state space approach. Traditional state space approach described in [28] is suitable to be introduced in fractional order dynamics. The approach is presented under the name “augmented system approach” [29, 30]. The stabilization issue of commensurate fractional order systems is studied using system augmentation, and used in [31, 32]. Fractional order tuning is performed in several recent works [33-35]. Therefore, the current study introduced in this paper designs a state space based fractional order integral controller. The proposed control scheme is compared to an integer order controller, and simulation results are shown.

The remaining part of the paper is organized as follows: Fractional order controller is designed in the next Section. Section 3 is dedicated to system description of linear servo cart unit and its model. In Section 4, the proposed control scheme is simulated for the position tracking and speed regulating of a linear servo cart system. Simulation results with comparison over integer order controller are presented in the same Section as well. Finally, the discussion and conclusion are addressed in Section 5.

2. Design of fractional order controller

Integral action based state feedback control is a very useful technique for set-point tracking application [36, 37]. State space model for integer order control of an LTI system can be represented by:

where, $x_s\left(t\right)\in R^n\text{,}$$u\left(t\right)\in R$, $q\left(t\right)\in R$ and $y_s\left(t\right)\in R$ are state vector, a control input, disturbance input and output variables, respectively. Further, $A\in R^{n\times n}$ is the plant dynamic matrix, $B\in R^{n\times 1}$ is the control input vector, $E\in R^{n\times 1}$ is disturbance matrix and $C$$\in R^{1\times n}$ is the output gain vector. The law of control with state feedback based integral action is expressed by:

where, $x_s\left(t\right)={\left[x_s\left(t\right)x_{sr}\right(t\left)\right]}^r$ is the augmented state vector and the output of integral operator is mentioned by $x_{sr}\left(t\right)$. This integral operator is produced through an integral control as shown in Fig. 1. The figure shows a control scheme based on state feedback with integer integral action. This control scheme helps to improve the quality of system response in terms of the steady-state error. For the computation of feedback gain vector $K_s$ and $K_r$, any suitable method, such as Ackermann's formula can be implemented.

Fig. 1Control scheme based on a state feedback with integer integral action

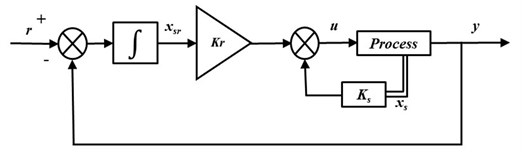
To implement fractional order control scheme, it is necessary to use fractional integrator 1/$s^{\alpha }$ instead of integer order integrator 1/$s$ ($\alpha$ being a rational number between 0 and 1). Again, the static gain $K_r$ should be replaced by a compensator $K\left(s\right)$. Further, $K_s$ is used to stabilize the system. Fractional order integrator 1/$s^{\alpha }$is cascaded with compensator $K\left(s\right)$ as shown in Fig. 2. The concept of Bode’s ideal transfer function [38] is the base to design this $K\left(s\right)$. The said transfer function is as follows:

where, $\gamma$ and ${\tau }_c$ are responsible for the overshoot and the behavior of transient response for set point tracking. This Bode’s ideal transfer function helps to eliminate steady-state error in the response. It also guarantees the robustness of process gain and ensures the iso-damping property of step response for a closed loop system. These properties are not obtainable while using traditional state feedback control scheme with integer integral control action [33-35].

From the known overshoot, non-integer order $\gamma$ can be calculated using the following equation which is referred from work of Barbosa et al. [39] and for more detail, one can see in [40, 41]:

Other way proposed in [38], can be implemented to calculate ${\tau }_c$ and $\gamma$ from gain crossover frequency, $\omega$ and phase margin, $\phi$. The required equations are as follows [29, 30]:

Fig. 2Fractional compensator based state space control [33-35]

It can be noted that the structure provided in Fig. 2 is suitable for both stable and unstable system due to its state feedback, $K_s$. It needs to design both integer filter $K\left(s\right)$ and $K_s$. Here the fractional integrator is cascaded by integer filter $K\left(s\right)$. Design steps are summarized in this paper, but the details are available in [35].

Now the law of control can be expressed for an LTI system as follows:

Let the above system is an integer order linear system. But to implement fractional action, a fractional derivative operator is introduced by the Eq. (8):

where, $r$ and $x_{sr}$ are reference set-point and new states produced through fractional order integral (1/$s^{\alpha }$), respectively (order $\alpha$ being a rational number between 0 and 1). The Fractional derivative operator is denoted by $D^{\alpha }$.$C\in R^{1\times n}$ is the output gain vector. $K_s$ is the gain vector need to be designed to place $n$ number of poles for the characteristic roots in the state feedback loop. Which can be stated in Eq. (9) and can be evaluated with the help of Ackermann's method [42]:

$K\left(t\right)$ of Eq. (7) is the impulse response of $K\left(s\right)$, which is an integer compensator. It can be computed as follows [35]:

where, $N\left(s\right)$ is the numerator of the transfer function of integer system described in Eq. (1), and ${\mathrm{\Delta }}_d\left(s\right)$ is loop characteristic polynomial of the inner loop described by the system and the state feedback vector $K_s$. Further, a low pass filter, $1/{(1+{\tau }_{f}s)}^j$ is cascaded to make it effective. It can be mentioned here that the order of the fractional integrator operator $\alpha$ is equal to the fractional order $\gamma$ of the reference model of Eq. (3).

3. Mathematical modeling of linear servo cart system

A linear servo cart system is shown in Fig. 3. The cart has the mass, $M_c$, velocity, $v_c$. The motor pinion of the cart is experienced by viscous damping force $B_c$, which is combined with other damping terms and obtained an equivalent damping coefficient, $B_q$. $F$ is the driving force generated by the servo motor. Therefore, Newton’s second law of motion is described as follows:

where:

Note that, ${\eta }_g$ is the efficiency of the gearbox, $k_g$ is gear ratio, ${\eta }_m$ is the efficiency of motor, $k_t$ is the motor torque constant, $k_m$ is back-emf constant, $r_{mp}$ is the radius of motor pinion, and $R_m$ is the motor resistance. Motor inductance is considered very low; therefore, it is ignored.

Now the driving force:

Here $v_m$ is applied voltage, and $A_m$ is actuator gain, which is obtained as $A_m={\eta }_g{k}_g{\eta }_m{k}_t/r_{mp}{R}_m$. Hence, the Eq. (11) expresses the complete dynamic behavior of cart velocity $v_c$ which is directly influenced by input voltage $v_m$. Therefore, the transfer function is obtained as follow:

From this transfer function, the steady sate gain and time constant are expressed as $K=A_m/B_q$ and $\tau =M_c/B_q$ respectively. Hence, the plant transfer function for cart speed to applied voltage is:

In Eq. (11), the inertial force due to motor armature is ignored. If this force is considered, then there will be only changes in time constant parameter and steady-state gain will remain unchanged such that:

where equivalent inertia term:

An integrator (1/$s$) can be cascaded with the speed transfer function to obtain the transfer function of voltage and cart position. The resulting transfer function becomes:

Fig. 3Typical linear servo cart system [43]

4. Simulation results

Model parameters of the plant is chosen such as actuator gain, $A_m=$ 1.727 N-m/V, equivalent damping coefficient, $B_q=$ 12.04 N-m-s/rad and equivalent mass in terms of armature inertia of motor, $J_q=$ 0.7031 kg. Hence, the time constant, $\tau$ and steady state gain $K$ is depicted as 0.0584 s and 0.143 m/s/V, respectively. Now the state space model of linear servo cart system is as follows:

The purpose of the control is to track the set-point of linear servo cart position, $x\left(t\right)$ and speed, $v_c\left(t\right)$. Transfer functions for cart position and speed corresponding to this model are:

and:

where, $K=$ 0.143 and $\mathrm{\Delta }\left(s\right)=s\text{0.0584}\text{+1}\text{.}$ The method discussed in Section No. 2 is implemented to solve the set-point tracking problem of linear servo cart system.

Since $G_x\left(s\right)$ represents 2nd order transfer function model, both roots are comprised to be a second order polynomial $p^2+2\zeta {\omega }_{n}s+{\omega }_n^2$ where $\zeta =$ 0.591 and ${\omega }_n=$ 26.0 rad/s, which complies with the expected time-domain specifications to control the position of linear servo cart system. In which, pick time $t_p=$ 0.15 s, percentage overshoot $PO=$ 10 % and steady state error, $e_{ss}=$ 0 are chosen. The state feedback $K_s$ is calculated for fulfilling these requirements such that:

Now the transfer function between input signal $r\left(s\right)$ and cart position output $x\left(s\right)$ of closed loop system is:

This transfer function shows corresponding poles at the denominator. Now it needs to find the characteristic polynomial of fractional controller. To obtain this, phase margin and gain crossover frequency are measured considering the open-loop transfer function related to $X\left(s\right)/r\left(s\right)$. The measured values are used in Eq. (5) and Eq. (6) to obtain the parameters $\gamma =$ 1.8657 and ${\tau }_c=$ 0.5 s of the characteristic polynomial to design the fractional controller. The fractional controller, $K\left(s\right)$ is designed with the help of Eq. (10). It is expressed as:

Here, $j=$ 1 because ${\mathrm{\Delta }}_d\left(s\right)$ is second order. A suitable value of ${\tau }_f$ is chosen as 0.005 s for the time constant of the filter in Eq. (26).

To prove the superiority of the proposed technique, integer order controller based on modified proportional derivative (PD) method is demonstrated as shown in Fig. 4. A high-pass filter with negative velocity feedback is incorporated in this integer order control scheme. The strategy of integer order control scheme, to be compared, is considered similar to the structure shown in Eq. (27):

where $k_p$ and$k_v$ are proportional gain and negative velocity feedback gain, respectively. $V_m$ is the control input and $x\left(t\right)$ is the position measured for linear servo cart system. With the help of characteristic equation for closed loop system and equating with the standard second order system, the gains $k_p$ and $k_v$ are calculated 275.49 V/m and 5.54 V-s/m, respectively.

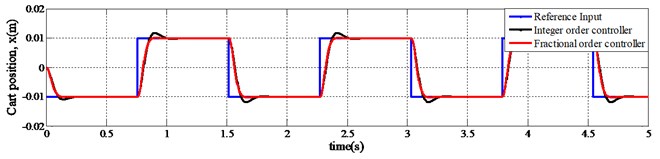
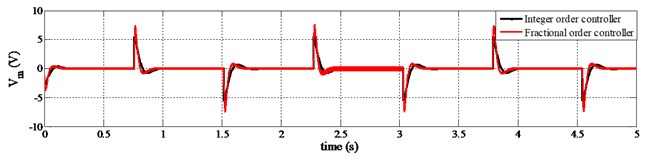
At first, the designed fractional order controller is evaluated and compared with integer order controller using simulation program for position tracking of a linear servo cart system. The position set-point of applied reference input changes such that, $x_c=$ –0.01 m at $t=$ 0 s and $x_c=$ +0.01 m at $t=$ 0.75 s. Square reference input signal is applied with one complete cycle time of 1.5 s. Fig. 5 represents the simulation results of position tracking performances for the linear servo cart system. The model used are described in Eq. (19) to Eq. (21). These results entail that, positions of linear servo cart are stabilized after some transient value, and then the cart tracks the set-point.

Although the duration of transient and steady state conditions is a fraction of a second, yet it is crucial for several complex applications like double or triple inverted pendulum, the inverted pendulum on seesaw, etc. A comparison is shown in this figure between integer order controller based PD compensator and fractional order controller. It is observed that the fractional order controller performed better than the integer order controller. Fig. 5 shows that; the position of the cart is disturbed using integer order controller when the set point is changing. But fractional order control laws provide no disturbance at all during the transition of set-point except some delay.

Fig. 4Block diagram of integer order control scheme

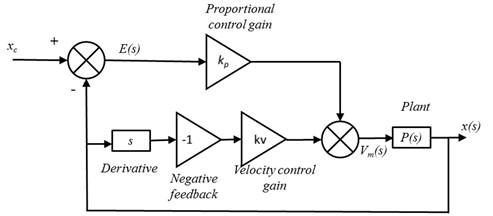
Fig. 5Position tracking control for a linear servo cart system

a)

b)

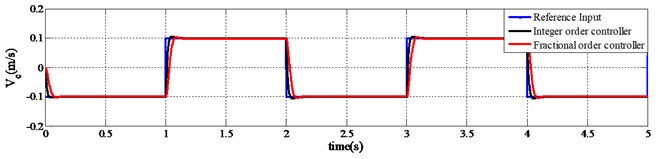
Further, the designed fractional order controller is evaluated and compared with integer order controller using simulation program for speed regulation of a linear servo cart system. The speed set-point of applied reference input changes such that, $V_c=$ –0.1 m/s at $t=$ 0 s and $V_c=$ +0.1 m at $t=$ 1.0 s. Step reference input signal is applied with one complete cycle time of 2.0 s. Fig. 6 represents the simulation results of the speed controller. It shows the performances of speed regulation of linear servo cart system. These results entail that, the speed of linear servo cart is perfectly following the set-point reference signal. A performance comparison is shown in the same figure between integer order controller and fractional order controller.

Fig. 6Speed tracking control for a linear servo cart system

a)

b)

It is observed that the fractional order controller performed well enough and almost similar to the integer order controller. Fig. 6 shows that, when the set point is changing, the speed of the cart is following the reference signal accordingly without any major overshoot except a slight delay.

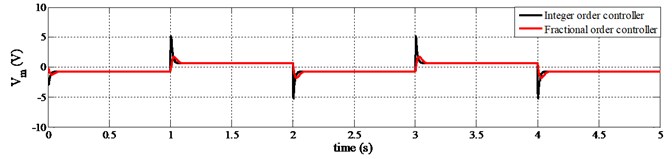
Again, in Fig. 5, the bottom one is showing the fluctuation of control voltage while the set-point changes. The amplitude of required control voltage is higher for fractional order control scheme than the integer one. However, the range of control voltage is still within the limit for both fractional and integer order controller. On the other hand, in Fig. 6, the amplitude of required control voltage for speed regulating of servo cart system is lower for fractional order control scheme than the integer one.

5. Conclusions

A fractional order controller is designed and simulated in this paper. Although, several research works are accomplished designing fractional order controller incorporating integral, proportional integral (PI), proportional derivative (PD) or proportional integral derivative (PID) controller to investigate the performance of different state variables of the system, but a little research is executed using state space approach to design fractional order controller. Therefore, the current investigation is conducted to observe the effect of fractional order controller using state space approach for the system’s performance in terms of position and speed tracking of a linear servo cart system. Linear servo cart system is a very powerful base unit to stabilize several highly unstable systems like double or triple inverted pendulum, double inverted pendulum with a flexible link, the inverted pendulum on seesaw, etc. Hence, the state space approach based fractional order controller is demonstrated here. Further, an integer order controller based on proportional derivative (PD) approach is also shown for comparison. Simulation responses are presented and analyzed. The comparative simulation results confirmed that the fractional order controller performed well then, the integer order controller while tracking the cart position and speed of a linear servo base system following a set-point reference input.