Abstract
Fatigue spalling is one of the main reasons for rolling element bearing fault. When spalling fault occurs in the bearing raceway and the rolling balls are in and outside the stripping, the vibration signal changes. When rolling elements enters the fault zone, a step response is generated, which mainly consists of lower frequency components. When rolling elements exits the fault zone, an impulse response is generated with a wide bandwidth. To effectively separate these two types of signal characteristics is important to measure the length of peeling zone for ceramic ball bearing. In our research, we proposed a method of double-shock feature extraction for peeling failure of hybrid ceramic ball bearing based on double tree complex wavelet packet transform (DTCWPT). Firstly, in order to enhance the Signal Noise Ratio (SNR), the original vibration signal was denoised by double tree complex wavelet packet transform; Then, separating and extracting double impulse characteristics of the vibration signal from the hybrid ceramic ball bearing with the spalling failure by using Hilbert transform envelope algorithm. Experimental results showed that this method can effectively separate the double impulse characteristics of the hybrid ceramic ball bearing fault.
1. Introduction
The hybrid ceramic ball bearings are widely used in high speed machine tools because of their high rigidity, high temperature resistance and high-speed conditions. However, its application is limited by lacking of relative method of fault detection and fault degree evaluation of hybrid ceramic ball bearings. Zhou Jingling et al. established the fatigue life model of silicon nitride ceramic ball rolling bearing and verified the main failure mode of silicon nitride ceramic ball bearing - fatigue flaking [1]. The length of the stripping zone is one of the most important features that characterizes the fault degree. Therefore, measuring the length of the stripping zone is of great value to evaluate the fault degree. The traditional way of measuring the length needs to remove the bearing from machine, which is unsuitable for operating conditions. But Randall et al. [2] improved the estimation of the length of the stripping zone under operating conditions by extracting the time interval of the double-impact characteristic [3]. This method provides new direction for calculating the length of the stripping zone under operation conditions.
The preliminary study of the project team found that the vibration response about the hybrid ceramic ball bearings peeling failure does exist double-impact feature [3]. However, the actual situation of rotating machinery is more complicated because of the multi-source mixed signal with lots of interference. Moreover, double-impact characteristics are easily flooded by strong background noise. Hence, it’s difficult to observe the double-impact characteristics directly from the original signal.
In order to effectively extract the double-impact characteristics caused by the spalling failure of the outer ring raceway of the hybrid ceramic ball bearing, we proposed a method of double-impact feature extraction based on dual-tree complex wavelet transform (DT-CWPT) for the outer ring fault of the hybrid ceramic ball bearing. Firstly, the original vibration signal is reconstructed by double tree complex wavelet packet, and the original vibration signal is denoised, then we used the Hilbert envelope extraction method to extract the double impact feature from the vibration signal of the hybrid ceramic ball bearings. Our result may provide solid foundation for the length measurement and the degree of failure evaluation.
2. Introduction about DT-CWT
2.1. The dual-tree complex wavelet transforms
The dual-tree complex wavelet transforms (DT-CWT) is proposed by Kinsbury et al. [4] and it has many advantages such as similar translation invariance, good direction selectivity, limited data redundancy, high computational efficiency and full weight structure. DT-CWT consists of two parallel discrete wavelet transforms. Two real wavelet transforms use real tree and imaginary tree to form a filter bank. Double tree complex wavelet can be expressed as:
where , represent two real waves in the formula, where is a complex number unit.
The double wavelet complex wavelet transform is composed of two parallel wavelet transforms, according to the wavelet theory: the wavelet coefficients and the scale coefficients of the real tree wavelet transform can be calculated by following two formulas:
Similarly, the wavelet coefficients and scale coefficients of the virtual tree wavelet transform are obtained:
The wavelet coefficients and scale coefficients of dual-tree complex wavelet transform are:
Finally, the wavelet coefficients and scale coefficients of the double-tree complex wavelet transform can be reconstructed by Eqs. (6) and (7):
2.2. Compared with the double-tree complex wavelet transform
Compared with the double-tree complex wavelet transform, the double-tree complex wavelet packet transform is a more sophisticated signal processing method. The double-tree complex wavelet transform does not further decompose the high frequency part of signal, while the double tree complex wavelet packet transform does [5].
The signal can be expressed as a reconstructed signal after a double tree complex wavelet packet transform:
From the Eqs. (8) to (10), it is clear that the reconstructed signal of the original signal can be expressed as:
2.3. The kurtosis
The kurtosis can be expressed as:
In this formula, is the amplitude of the vibration signal; is the mean of the amplitude of the vibration; is the probability density function; is the standard deviation.
Fig. 2Double impulses phenomenon illustration caused by peeling off the bearing outer ring
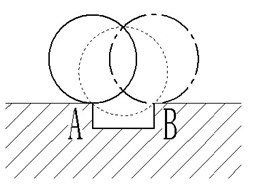
Fig. 3The artificial spall of outer race (0.5 mm)

3. Introduction to the research of Double Impact features
3.1. Fault bearing’s double impact features
When the rolling bearing raceway’s flaking failure occurs, the rolling body passes through the peeling area, leading to double impact features. The double impact of rolling bearings was first proposed by Epps [7] in 1991 and thoroughly discussed since then.
As shown in Fig. 2, when the rolling bearing’s flaking failure occurs, the rolling body will be contacted with the edge of the stripping area during operation, which is called getting into the stripping area when contact with A. Meanwhile, it is called exit the stripping area when contacted with B. Epps considered that the vibration signals between the rolling body into and out of the stripping area are different when the flaking failure occurs. Dowling [8] pointed out that the vibration signals of the rolling body into and out of the stripping zone are pulse corresponding, and the phase difference between the entry point and exit point is 180 degrees. Sawalh’s [2] studies have shown that the rolling force gradually reduced with the process of getting into the stripping area, the response features is step response; when the rolling body contacts with B point, the direction between the rolling force and the speed are opposite, which will cause a more violent impact, the response features is impulse response. In Fig. 2, when the rolling element reaches the dotted line, the center of rotation is changed from A to B, at the same time the rolling element also rolls over half of the length of the stripping zone. When reaching the position indicated by point line, the rolling body is completely left from the flaking area.
But the double-impact feature itself is relatively weak and susceptible to background noise and other factors, the original vibration signal is quite complicated, and we usually need to apply the appropriate signal processing method to the original vibration signal so that the double impact can be completely separated and extracted.
3.2. Double impact characteristics of ceramic ball bearings
The vibration signal collected in this paper is for the case of a Hybrid ceramic ball bearing with a speed of 586 r/min and an outer ring stripping fault size of 0.5 mm. In order to better simulate the working condition, the Gaussian white noise with SNR of –4 dB was added to the collected vibration signal. The time domain signal is shown in Fig. 4(a).
Fig. 4Waveform of original signal
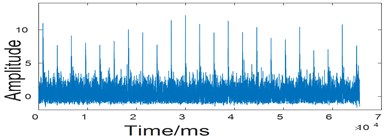
a) Double impulses characteristic waveform under 586 r/min
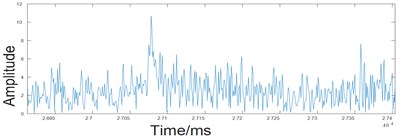
b) Enveloped signals based on Hilbert
4. Double impact feature extraction method based on double – tree complex wavelet packet transform
Based on the double-tree complex wavelet packet transform, the double-shock feature extraction method has the following steps
1) Firstly, the original signal which was collected is decomposed by double-tree complex wavelet packet to obtain the wavelet signal;
2) Calculating the kurtosis values of the wavelet signals of each node and the average of these kurtosis values;
3) Comparing the kurtosis value and the average value of each signal after the decomposition, and the signal whose kurtosis value is larger than the average value is reconstructed. the signal whose kurtosis value is smaller than the average value is set to zero;
4) Obtaining the envelope spectrum of the reconstructed signal obtained in step (3).
5) Extracting double impact features.
5. Test analysis
The test bench used in the study was QPZZ-II fault simulation test bench, as shown in Fig. 5. A hybrid ceramic ball bearing with a single fault feature of the outer ring is installed in the bearing seat. Rolling bearing is installed in the simulation test bench, the outer ring is fixed, the inner ring is free to turn.
By using the method proposed in this paper, the original signal is decomposed by four wavelet packets, and the original signal is decomposed into 16 wavelet packet nodes. The kurtosis value and the average of these kurtosis values are calculated. Compare the kurtosis value and the average value of each signal after the decomposition, and the signal whose kurtosis value is larger than the average value is reconstructed. the signal whose kurtosis value is smaller than the average value is set to zero. The kurtosis values and the mean values are shown in Table 2.
Fig. 5QPZZ-II test rig

Table 1The experimental parameters
Bearing type | Size | Speed | DAQ | Sampling rate | Sensor model |
6205 | 0.5 mm | 586 r/min | NI-USB9215 | 100 kHz | DH112 1205173R |
Table 2Kurtosis values and their mean values for each node signal
No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Means |
Real | 5 | 4 | 5 | 8 | 3. | 3. | 3 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3.7 |
Imaginary | 5 | 4 | 4 | 8 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3.6 |
It is shown from Table 2 that the average value of the real part kurtosis of each node signal after decomposition is 3.7, Then 5, 6 ... 15 and other kurtosis values which is less than the average value of the signal set to zero. Keep 1, 2 ... 8 and so on. After decomposition, the average value of the imaginary part of the node signal is 3.6. Then set the value which is 5, 7 ... 16 and so on to zero. And then reconstructed the signal after zeroing with the signal of the kurtosis value greater than the mean of the kurtosis value together. the denoising signal which is reconstructed is shown in the following figure. Waveform and partial magnification that is obtained by envelope spectrum of the reconstructed signal is shown in Fig. 6.
Fig. 6Waveform of reconstructed signal
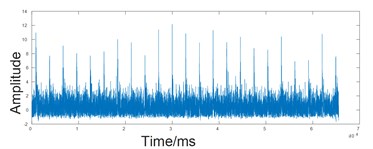
a) Processed signal
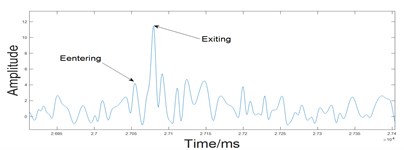
b) Double impulse characteristic signal
Fig. 6 showed that after using the method proposed by this paper we can clearly see the double-impact features when the rolling body enter and exit peeling zone. So that we can extract double impact Feature of hybrid ceramic ball bearings.
6. Conclusions
During the hybrid ceramic ball bearings running, which has an outer ring peeling fault, when the rolling body enters and exits the peeling zone, the double impact feature of the acceleration vibration signal is submerged under the noise, and is difficult to extract and analyze directly. Combining the kurtosis value calculation of the vibration signal, the vibration signal of the Hybrid ceramic ball bearings with the outer ring peeling fault is decomposed by the double tree complex wavelet packet based on the double tree complex wavelet packet transform. According to the kurtosis value, we set them to zero and reconstruct. Th’is method can be used to efficiently filter interference signal which is influent by the factors such as the vibration source, strong background noise and signal transmission path and so on in the process of mechanical operation. So, that we can achieve hybrid ceramic ball bearings double impact features extraction, which provides a new way to realize the measurement of the length of the stripping zone under working condition. The experiment proves the effectiveness of the method.
References
-
Zhou Jing Ling, Wu Guo Qing, Chen Xiao Yang Tensilestress life model for rolling contact fatigue of silicon nitride ceramic balls. Journal of Mechanical Engineering, Vol. 44, Issue 2, 2008, p. 37-42.
-
Sawalhi N., Randall R. B. Vibration response of spalled rolling element bearings: observations, simulations and signal processing techniques to track the spall size. Mechanical Systems and Signal Processing, Vol. 25, Issue 3, 2011, p. 846-870.
-
Kong You Bing, Guo Yu, Wu Xing Double-impulse feature extraction of faulty hybrid ceramic ball bearings based on EEMD. Journal of Vibration and Shock, 2016.
-
Kingsbury N. G. The dual-tree complex wavelet transform: a new technique for shift invariance and directional filters. IEEE Digital Signal Processing Workshop, 1998.
-
Bayram I., Selesnick Ivan W. On the dual-Tree complex wavelet packet and M-Band transforms. IEEE Transactions on Signal Processing, Vol. 56, Issue 6, 2008, p. 2298-2310.
-
Antoni J., Randall R. B. The spectral kurtosis: application to the surveillance and diagnostics of rotating machines. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 308-331.
-
Epps I. K. An Investigation into Vibrations Excited by Discrete Faults in Rolling Element Bearings. Ph.D. Dissertation, University of Canterbury, Christchurch, New Zealand. 1991.
-
Dowling M. J. Application of non-stationary analysis to machinery monitoring. IEEE International Conference on Acoustics, Speech, and Signal Processing, 1993, p. 59-62.
About this article
Project supported by the National Science Foundation of China (Grant No. 51365023).
