Abstract
Electro-mechanical actuators (EMAs) are increasingly being used as critical actuation devices of the aircraft. It will cause serious accidents once the fault of EMAs occurs, thus the fault diagnosis of EMAs is essential to maintain the normal operation of aircraft. In this paper, a method based on WPD-STFT time-frequency entropy and PNN is proposed to achieve fault diagnosis of EMAs by processing the vibration signals collected by the accelerometer installed in the EMAs. Firstly, the vibration signals are decomposed by wavelet packet to obtain the signal components of different frequency bands, the signal components are subjected to STFT and spectrograms are obtained. Then, time-frequency entropy is calculated and combined with principal component analysis (PCA) for dimension reduction as the feature vector. Finally, the probabilistic neural network (PNN) classifier is introduced to classify the fault modes. The experimental result shows that this method can accomplish the accurate fault diagnosis of EMAs. Moreover, the performance of the proposed WPD-STFT time-frequency entropy method has an advantage over that of WPD-PCA method or STFT combined with mass-moment entropy method for feature extraction.
1. Introduction
There is an increasing development trend to move to fly-by-wire control and away from the traditional hydraulic actuator system. As one of the important development directions, electro-mechanical actuator (EMA) has a lot of advantages, such as compact structure, high reliability, lighter weight and lower fuel consumption, and it is more and more widely applied to the aircraft's critical components. So, the operating condition of the EMA plays a key role in the safety of the aircraft and the completion of the mission, and an undetected failure of the actuator may cause serious consequences. Therefore, it is of great significance to research the fault diagnosis and prognosis of EMAs.
NASA Ames Research Center's members are dedicated to the research of PHM system for EMAs, the researchers presented a fault diagnostic algorithm combined model-based method and data-driven method, and achieved fault diagnosis of the EMAs [1]. In order to validate the diagnostic algorithm with realistic data, they designed the Flyable Electro-mechanical Actuator (FLEA) test-bed, and conducted experiments in both laboratory and the UH60 helicopter [1]. A method based on the combination of GM (1, 1) with improved EMD, and a method based on Wavelet Transform (WT) are both used for fault diagnosis of motors in EMAs [2, 3].
Although the fault diagnosis for some components of EMAs has been carried out, the diagnosis of the overall structure of EMAs based on the analysis of vibration signal has not been fully realized. There have been many data-driven methods for signal analysis in recent years [4], and a method based on WPD-STFT time-frequency entropy and PNN is proposed for fault diagnosis of EMAs in this paper. The vibration signals are decomposed by wavelet packet, and signal components of different frequency bands can be obtained. The STFT is performed for signal components to obtain the spectrogram. Then time-frequency entropy of spectrogram is calculated, and combined with PCA for dimension reduction. Finally, the PNN classification model is trained to realize fault classification. The method proposed can realize the accurate fault diagnosis of the EMAs.
2. Feature extraction based on WPD-STFT and time-frequency entropy
2.1. Time-frequency analysis based on WPD-STFT
2.1.1. Short-time Fourier transform (STFT)
The short-time Fourier transform is developed on the basis of Fourier transform. This time-frequency analysis method selects a fixed window function and assumes that the signals are stable in it. Then the signals are segmented by moving the window function, and the segmented signals are subjected to Fourier transform respectively. STFT can solve the problem that traditional Fourier transform lacks the partial analysis, and it is more suitable for analysis of non-stationary signal.
The STFT of signal which is used as window function can be expressed as:
The time-frequency energy spectrum can reflect the time-frequency distribution of the signal, which can be expressed as the modulus of the STFT function:
2.1.2. Wavelet packet decomposition (WPD)
Wavelet packet decomposition is an extended method based on wavelet analysis which can decompose signals more meticulously. WPD can decompose the low-frequency part and high-frequency part of signals at the same time, then the signal components of different frequency bands can be obtained by reconstructing the decomposed wavelet coefficients. Therefore, WPD has stronger ability of signal analysis with higher time-frequency resolution.
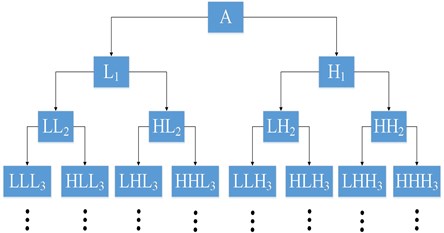
The decomposition process of the wavelet packet is shown in Fig. 1, is the original signal, is the low frequency part, is the high frequency part, and the sequence number is the number of decomposed layers of the wavelet packet.
Fig. 1Decomposition process of the wavelet packet
2.1.3. WPD-STFT method
In this paper, WPD and STFT are combined for time-frequency analysis. So that the signals can be decomposed more detailedly, and the time-frequency analysis can be more effective.
2.2. Time-frequency entropy
The time-frequency distribution obtained by the WPD-STFT method can describe the energy variation at the different frequencies of the signals during the sampling time, and the time-frequency distributions in the normal and fault states are often different. In order to quantitatively describe the degree of difference, the information entropy theory is introduced into the time-frequency analysis. The information entropy can describe the uniformity of the probability distribution, and the uniformity of the energy distribution in spectrogram reflects the operating state of the EMAs.
The spectrogram is divided into blocks with equal areas, the energy in each block is , and the energy of the whole time-frequency plane is . The energy of each block is normalized as:
According to the definition of information entropy, the time-frequency entropy of the signals is defined as:
3. Fault classification based on PNN
Probabilistic neural network (PNN) is a feedforward neural network developed by radial basis network based on Bayesian minimum risk criterion. The network has the advantage of short training time and the ability to avoid falling into the local minimum, which is suitable for solving the problem of mode classification.
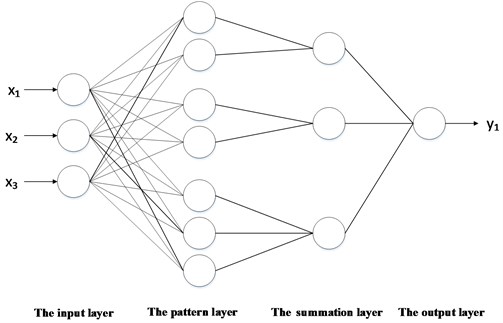
PNN is generally composed of the input layer, the pattern layer, the summation layer and the output layer, and the basic structure (taking 3-dimensional input vectors as an example) is shown in Fig. 2.
The input layer accepts the values from the training samples and passes the feature vectors to the network. The pattern layer calculates the matching relation between the feature vectors and the patterns of the training samples. The summation layer sums the probability of belonging to a certain fault mode to obtain the estimated probability density function of the mode. According to the estimated probability density function, the output layer selects a neuron with the highest probability as the output of the system.
Fig. 2Basic structure of probabilistic neural network
4. Case study
The data used in this paper is the open source data of NASA website. It is the data collected by NASA Ames research center from the FLEA test-bed. Four typical fault modes of critical components are selected, which are ballscrew return channel jam, screw surface spall, motor failure, position sensor failure. The vibration signals were collected at a sampling frequency of 20 kHz in five states (normal and four fault states), and 116 sets of data (5000 sampling points per set) were selected to analysis for each state.
4.1. Feature extraction of the vibration signals
First of all, the original vibration signals are normalized for data preprocessing, so that the subsequent data processing can be more convenient and accurate. Secondly, the data of each fault mode is decomposed to three layers by wavelet packet, and eight signal components from low frequency to high frequency are obtained. Then the STFT is performed to signal components, and the spectrogram can be obtained. The spectrogram of the first signal component for ballscrew return channel jam is shown in Fig. 3.
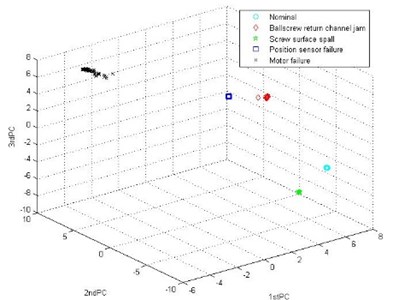
The 8-dimensional time-frequency entropy of the spectrogram for each state is calculated as the feature vector. And the feature vectors can be reduced to 3-dimensional vectors by PCA. The clustering result of the feature vectors is shown in Fig. 4.
Fig. 3Spectrogram of the first signal component of ballscrew jam
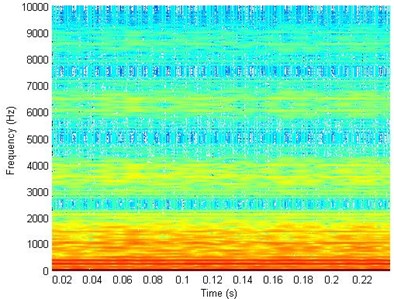
Fig. 4Clustering result of the fault features
4.2. Fault classification based on PNN
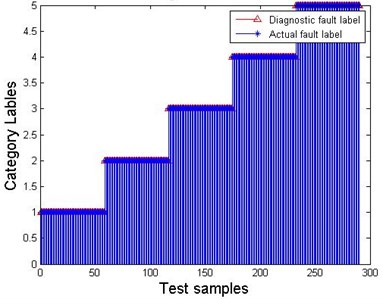
The PNN classification model is trained to classify the fault modes. Firstly, the first 58 sets of the feature vectors extracted from each mode are used as the training data, and the last 58 sets are used as the testing data; then the training data is used to train the PNN classifier; finally, the trained PNN classifier identifies the category labels of the testing data, and the final fault diagnosis result can be obtained. The classification result of the testing data is shown in Fig. 5, which shows the excellent classification ability of PNN.
Combining Fig. 4 and Fig. 5, it is proved that the proposed method can accurately diagnose the EMAs and has high diagnostic precision.
5. Comparison between the proposed method with WPD-PCA method and STFT combined with mass-moment entropy method for feature extraction
This section shows the comparison of the feature extraction method proposed in this paper with the other two methods.
Fig. 5Classification result of the testing data
The first one is a widely used method based on WPD-PCA. The vibration signals are decomposed by wavelet packet to obtain the eight signal components of different frequency bands. And the normalized energy of each signal component is used as the feature vector. Then the feature vectors are being reduced to 3-dimension vectors by PCA. The clustering result is shown in Fig. 6. It can be seen that the feature scattered points of different states obtained by WPD-PCA method are too close, so that it is difficult to classify the fault modes accurately.
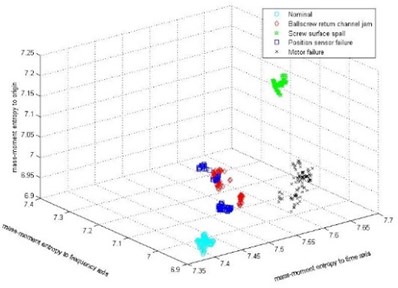
The second one is the method based on STFT combined with mass-moment entropy. The vibration signals are subjected to STFT and spectrogram can be obtained. Then the mass-moment entropy of the time-frequency plane to the time axis, the frequency axis and the origin are calculated respectively as feature vectors. The clustering result is shown in Fig. 7 which can verify that the feature vectors obtained by this method is difficult to classify.
It can be seen from the comparison results that the proposed method in this paper can extract the more sensitive features of EMAs so that the more accurate fault diagnosis can be carried out.
Fig. 6Clustering result of WPD-PCA method
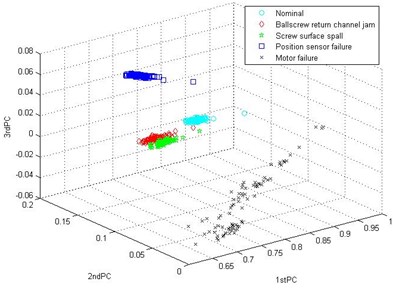
Fig. 7Clustering result of STFT combined with mass-moment entropy method
6. Conclusions
EMAs are increasingly applied to the critical components of the aircraft, so the research of fault diagnosis for EMAs is significant. In this paper, a data-driven method is proposed to diagnose the faults of main structures of EMAs including motor, ballscrew and position sensor. By analyzing the vibration signals of EMAs, the perfect diagnosis result is obtained, which proves that the method proposed in this paper can be effectively applied to the fault diagnosis of EMAs. Future work will concentrate on the research of other methods for fault diagnosis and prognostics of EMAs.
References
-
Balaban E., Saxena A., Narasimhan S., et al. Prognostic health-management system development for electromechanical actuators. Journal of Aerospace Information Systems, Vol. 12, Issue 3, 2015, p. 329-344.
-
Liu J., Zhang L., Li H. Application of GM(1, 1) model and improved EMD in fault diagnosis of airborne direct-driven electro-mechanical actuators. Journal of Grey System, Vol. 25, Issue 1, 2013, p. 24-31.
-
Xiao Lei, Li Yinghui, Zhao Kun, et al. Fault diagnosis of aircraft power actuation system based on wavelet transform. Journal of Air Force Engineering University, Natural Science Edition, Vol. 10, Issue 5, 2009, p. 55-58.
-
Sun J., Lu C., Ding Y. Fault diagnosis for hydraulic pump based on intrinsic time-scale decomposition and softmax regression. Vibroengineering Procedia, Vol. 10, 2016, p. 229-234.
Cited by
About this article
This study is supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-17-BJ-J-42 and YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51605014 and 51575021), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
