Abstract
In this paper, a rolling bearing fault detection method based on Local Characteristic-scale Decomposition (LCD) and Teager Energy operator (TEO) is proposed. Vibration signals is related to the bearing fault. However, the vibration signal of rolling bearing is nonlinear and has multiple components, which makes it difficult to analyze the signals by using traditional method such as the fast Fourier transform (FFT). LCD, a recently developed signal decomposition method, is especially capable for dealing with the complex signal by decomposing it into several intrinsic scale components (ISC). Furthermore, to extract fault diagnosis of the components, we used TEO to demodulate each ISC. The energy of fault feature frequencies was extracted as fault vector. The result shows that the method successfully diagnoses bearing fault.
1. Introduction
As an important part of rotating machinery, rolling bearing keeping it away from being failure is a necessary prerequisite for machinery to work normally [1]. But the uncertainty of bearing life caused by frequent faults makes it difficult to manage the health condition of rolling bearing. As a result, it is an important subject to analyze the bearing fault in the area of rolling bearing fault diagnosis. The vibration signals have some information about bearing fault [2]. However, the nonlinear and non-stationary characteristic of vibration signals increases the difficulty of extracting information from the signals. Traditional method like Fast Fourier Transform (FFT) can only deal with linear and stationary signals, and can hardly effectively analyze vibration signals [3]. Time-frequency based methods such as Hilbert-Huang Transform and Wavelet Transform have been widely adopted to detect faults of rolling bearing. Among them, empirical mode decomposition (EMD), a self-adaptive method, has been widely utilized since it was proposed by N. E. Huang in 1998. Complex signals with the nature of nonlinear can be decomposed into linear superposition of intrinsic mode functions (IMFs). By using Hilbert-Huang Transform on IMFs, the information of instantaneous amplitude and instantaneous frequency can be easily extracted. But EMD has some limits such as mode mixing and endpoint effects caused by multiple iterations. A new developed method called local characteristic-scale decomposition (LCD) can reduce the effect of endpoint and mode mixing. Accordingly, LCD is adopted to decompose the signals [4].
Teager energy operator (TEO) was first presented by H. M. Teager and improved by Kaiser. At first TEO was used to process voice signals [5]. It’s a type of nonlinear differential operator which can calculate the total energy, including kinetic energy as well as potential energy, produced by the signal source [6]. The TEO can extract the transient characteristics of the signal, making it suitable for detecting the impact signal. For this reason, TEO was used to extract the cyclical shock feature of a bearing fault from the bearing vibration signals.
Considering the advantages of LCD and TEO, a new method based on LCD-TEO is proposed to extract the characteristic frequencies, so as to detect the rolling bearing fault.
The content of this paper is as follows. Section 2 introduces the principles of method based on LCD-TEO and shows results of the experiment. Section 3 analyses the results and receive the conclusion which can prove the validity of the method.
2. Detection method based on LCD-TEO
2.1. Description of LCD
LCD defines a signal component-intrinsic scale component (ISC), whose instantaneous frequency has a physical meaning. The signal component satisfying the conditions which are summarized below is the ISC.
(1) In the whole data segment, any adjacent extremum points are distributed between two segments of the time axis, monotonic between two extremes.
(2) Assuming that the absolute points are and the extreme time corresponds to the time axis coordinate , where 1, 2, 3…., and assuming that the point A in the extreme points are (, ). We get the following formula:
and with satisfy the following equation:
where is a constant between 0 and 1, in a sinusoidal signal a usually take 0.5. Satisfying the above two conditions is equivalent to ensuring that there is a single mode between the adjacent extremum of the component. The instantaneous frequency of the component has a physical meaning.
The signal is decomposed by the following method.
(1) Set the parameter and find all the extremes . Supposing that there are :
(2) Splicing all together to get , the original signal minus and get the component signal . If satisfies the conditions above, then it is the . Repeat the operation above until the separated signal is a monotonic signal. In this way can we get many ISCs.
2.2. description of TEO
For any signal , TEO is defined as follow:
The result of the TEO is the total energy of the signal.
2.3. The process of handling the signal
In this paper, the bearing vibration data is from the Bearing Data Center of Case Western Reserve University. The data are acquired under the condition of normal, inner-race fault, outer-race fault, and rolling element fault. The fault characteristic frequency of the bearing is provided in Table 1.
Table 1Characteristic frequency of the bearing
Race (r/min) | Load (HP) | Characteristic frequency of the bearing | ||
Inner / Hz | Outer / Hz | Rolling element / Hz | ||
1730 | 3 | 142.6356 | 88.02817 | 114.97 |
1750 | 2 | 144.2846 | 89.04583 | 116.2992 |
1772 | 1 | 146.0984 | 90.16527 | 117.7612 |
1797 | 0 | 148.1597 | 91.43735 | 119.4226 |
The original signal (outer race fault) is decomposed by LCD and we get many ISCs. The time-frequency map can be seen in Fig. 1. ISC1, ISC2 and ISC3 are chosen to be demodulated with TEO and we get the total energy of all the ISCs. The feature frequencies are obtained from the FFT of TEO. The frequency is depicted in Fig. 2, Fig. 3 and Fig. 4. We can see from the results that the characteristic frequency is around 90 Hz. It is consistent with the fault condition.
Fig. 1Time-frequency plot of ISCs
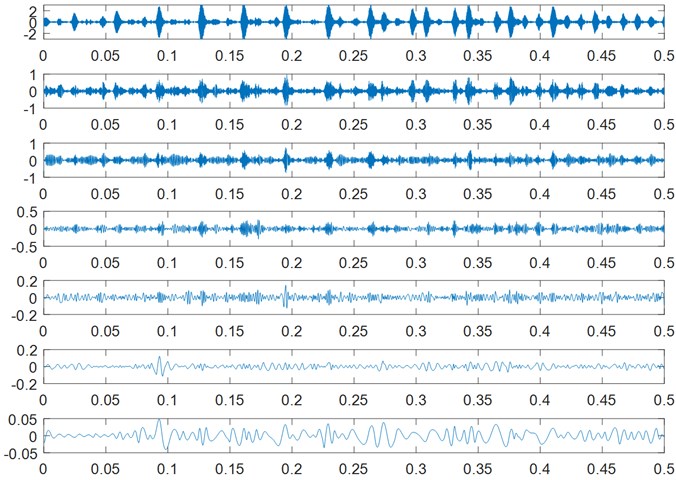
Fig. 2ISC1 instantaneous amplitude from LCD-TEO
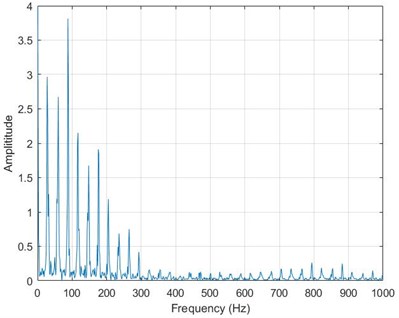
Fig. 3ISC2 instantaneous amplitude from LCD-TEO
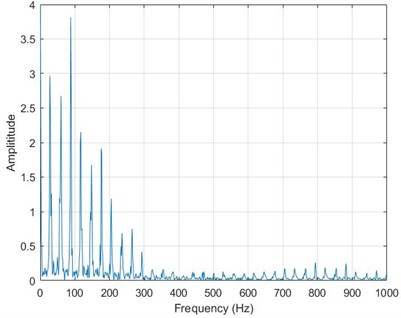
Fig. 4ISC3 instantaneous amplitude from LCD-TEO
3. Conclusion
The method based on LCD-TEO and used to extract the impact components of bearing fault is proposed in this paper. Firstly, the multi-component vibration signal is decomposed by LCD and the multiple ISCs are obtained. In the process of signal decomposition, LCD shows the advantages of rapid operation. TEO is used to extract the shock signal which is not prominent in the vibration signal. After comparison, it is found that the characteristic frequency of the fault signal is successfully extracted. In short, the LCD-TEO based method extract the information of the bearing fault from the signal successfully and the accuracy is very high.
References
-
He L. Research on Rolling Element Bearing Diagnosis Method Using EMD. Dalian University of Technology, 2012.
-
Li G., Li F. Application of STFT in the field of aero-engine vibration signal processing. Measurement and Control Technology, Vol. 32, Issue 4, 2013, p. 45-49.
-
Khan A. F. Condition monitoring of Rolling Element Bearing, A Comparative Study of Vibration Based Techniques of Windsor. Ontario, 1990.
-
Wang Q. H., Zhang X. B. Application of fractal theory to fault diagnosis for hydraulic pump. Journal of Dalian Maritime University, 2004.
-
Kaiser J. F. On a simple algorithm to calculate the “energy” of a signal. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’90), Vol. 1, 1990, p. 381-384.
-
Potamianos A., Maragos P. A comparison of the energy operator and the Hilbert transform approach to signal and speech demodulation. Signal Processing, Vol. 37, Issue 1, 1994, p. 95-120.
About this article
This study is supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-17-BJ-J-42 and YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51605014 and 51575021), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
