An analytical modeling for high-velocity impacts on woven Kevlar composite laminates

Fangyu, Chen; Li, Zhou; Yihao, Tang; Xiaoming, Zhou

doi:10.21595/jme.2017.19253

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: 31 December 2017

Check for updates

An analytical modeling for high-velocity impacts on woven Kevlar composite laminates

Chen Fangyu¹

Zhou Li²

Tang Yihao³

Zhou Xiaoming⁴

^{1, 2}State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing, China

^{3, 4}China Helicopter Research and Development Institute, Jingdezhen, China

Corresponding Author:

Zhou Li

Cite the article Download PDF

Downloads 1789

WoS Core Citations 1

CrossRef Citations 2

Abstract

In this paper, an analytical model, which based on energy balance, is built to study the process of high velocity impacts on woven Kevlar composite laminates by a cylindrical projectile. Four different mechanisms, such as laminate crushing, linear momentum transfer and tensile fiber failure, and shear plugging, is absorbed by the laminate while impacting. Then, simplification of the model is done to obtain the residual velocity and ballistic limit. The analytical results are validated with the results of experiment, and the perturbation analysis is done to analyze the reason of error.

1. Introduction

Resistance to ballistic impacts is an important requirement in many industrial applications, such as car, space shuttle and aeronautical industry. Woven fabrics are well-known to be good choice to resist ballistic impacts [1-3]. In the past, several researches have been focused on the impact on composite laminates. Elasticity method [4-7] was widely used to predict the behavior of impact. Three phases, which namely indentation, perforation and exit, are divided in the impact event by Zhu et al. [4]. Sun et al. [5] applied different criteria to obtain damage initiation, progression and plug formation. Wen et al. [6, 7] applied projectiles with different shapes to investigate FRP laminates’ perforation and penetration. Another method to predict the behavior of impact was the energy method. The projectile’s residual velocity and ballistic limit are calculated by energy balance equation. Naik et al. [8] and Xuan Haijun et al. [9] study the perforation of the composite plates with all the damage mechanisms and verified the analytical results with experimental results. Impact test is done by Ganesh Babu et al. [10] using different shape projectiles on unidirectional glass/epoxy composite plates. Sikarwar et al. [11, 12] and Wang Yuanbo et al. [13, 14] studied the analytical and experimental results of the residual velocity and ballistic limit of glass/epoxy and Kevlar/epoxy composite laminates respectively, which are subjected to high velocity impact. Yahaya et al. [15] observed a linear increasing tendency of energy absorption against impact velocity for Kevlar-Kenaf hybrid woven composites. Gu Xingjin et al. [16] and Michele et al. [17] calculate energy absorbed in different mechanisms with flat-end cylindrical projectiles. Chen et al. [18] studied simulation and experimental results of damage and energy absorption behavior for woven composites under ballistic impact. The researches mentioned above spend a lot of attention to high precision of the solutions of different equations, so they are high cost. To make a quick assessment at early stages of the design process, Lopez-Puente et al. neglect elastic deformation contribution in impact event [19] and then proposes a low-cost model and obtains closed-form solution to predict the ball projectile’s residual velocity after impacting on thin CFRPs woven laminated plates [20], but the influence of shear plugging [21-23] is not considered in their research.

In this paper, an analytical model is proposed to build the energy balance equation and predict the residual velocity of a cylindrical projectile after impacting at woven Kevlar composites. Simplification of the model is done to obtain the residual velocity and ballistic limit. Also, three dimensionless variables are built to simplify the process of analysis perturbation, which caused by tensile fiber failure. Analysis is done to explain the error between the results of calculation and experiment [13]. The model is low-cost, and its predictive accuracy is improved. The method of simplification could be useful in preliminary assessment of engineering.

2. Analytical model

The analytical model is built by terms of energy balance. In Lopez-Puente et al.’ [17] opinion, the kinetic energy of the projectile $E_{k}$ is absorbed by the laminate through three different processes. $E_{c}$ is the energy of crushing, which leads to laminate breakage. $E_{m}$ is the energy of linear momentum, transferred from the projectile to the detached part of laminate. $E_{f}$ is the energy of tensile fiber failure breakage. Elastic deformation energy is not considered by them in this analytical model. Naik et al. [19, 20]and Brenda et al. [21] consider that $E_{s p}$ , the energy absorbed by shear plugging, is also an important process. So, the basic balance equation can be presented in the following because of the influence of the shear plugging:

1

- d E_{k} = d E_{c} + E_{m} + d E_{f} + d E_{s p} .

Following each energetic term of Eq. (1) is presented.

The kinetic energy of the projectile is expressed as:

2

d E_{k} (x) = \frac{1}{2} m_{p} d (v {(x)}^{2}),

where $x$ is the distance between the position of the projectile and the impact surface of the composite laminate, $m_{p}$ is the mass of projectile, and $v$ is the velocity varies with the position.

The energy of laminate crushing is expressed as:

3

d E_{c} (x) = σ_{c} A (x) d x,

where $A (x)$ is the frontal projectile area that contacts the non-crushed laminate and $σ_{c}$ is the out-of-plane compressive strength of the laminate. Here, $A (x) = π r^{2}$ , where $r$ denotes the radius of the projectile cross-section.

The energy of linear momentum transfer is expressed as:

4

d E_{m} (x) = \frac{1}{2} (A (x) d x ρ) v^{2} (x),

where $ρ$ is the density of laminate.

The energy of tensile fiber failure is expressed as:

5

d E_{f} (x) = ω_{f} d V,

where $ω_{f}$ is the specific energy and $d V$ is the affected material volume at any $d x$ . The specific energy is estimated as:

6

ω_{f} = 2 (\frac{1}{2} X_{t} ε_{f}),

where $X_{t}$ is the tensile strength in fiber direction and $ε_{f}$ is the ultimate strain. Experimental result [9, 20] shows that the transverse section of laminate is a truncated pyramid, with a semi-angle $α$ and $β$ , and its diagonals aligned in the fiber directions. The upper base semi-diagonal is $r$ and the lower base semi-diagonal is $L = r + (h - x_{0}) t a n α$ with $x_{0}$ the position of the projectile at the time $x_{0}$ , as Fig. 1 shown. The affected material volume $d V$ is given by:

7

d V = 2 l \times l_{w} d x = 2 d x {(r + (h - x_{0}) t a n α)}^{2} t a n β,

and the energy of tensile fiber failure is given by:

8

d E_{f} (x) = 2 X_{t} ε_{f} {(r + (h - x_{0}) t a n α)}^{2} t a n β d x .

The value of $x_{0}$ can be obtained from following equation:

9

\int_{0}^{x_{0}} \frac{d x}{v (x)} = \frac{2 h}{\sqrt{E_{3} / ρ}},

where $h$ is the thickness of laminate and $E_{3}$ is the elastic modulus through-thickness.

Fig. 1Woven composite with cylindrical projectile

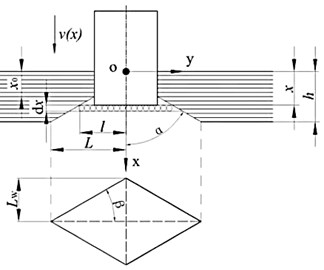
Tensile fiber failure happens while $x_{0} < x < h$ , so a function $C_{r} (x)$ is defined as follow to multiplies the last equation:

10

C_{r} (x) = \{\begin{array}{l} 0, 0 < x < x_{0}, \\ 1, x_{0} < x < h, \\ 0, x \geq h . \end{array}

The energy absorbed of shear plugging is expressed as:

11

d E_{s p} (x) = S_{s p} S (x) x d x,

where $S_{s p}$ is shear plugging strength and $S (x)$ is the cross-section perimeter of the projectile. Here, $S (x) = 2 π r$ .

While $x \geq x_{0}$ , the crushing energy and shear plugging energy have no influence. So, a function $C_{s} (x)$ is defined as follow to multiply the Eq. (3) and Eq. (4):

12

C_{s} (x) = \{\begin{array}{l} 1, 0 < x < x_{0}, \\ 0, x \geq x_{0} . \end{array}

3. Model simplification

As analysis above, the basic balance equation can be written as:

13

- \frac{1}{2} m_{p} d (v {(x)}^{2}) = σ_{c} A (x) C_{s} (x) d x + \frac{1}{2} (A (x) d x ρ) v^{2} (x)

+ 2 X_{t} ε_{f} {(r + (h - x_{0}) t a n α)}^{2} t a n β C_{r} (x) d x + S_{s p} S (x) x C_{s} (x) d x .

To solve the equation, some simplifications are made and the initial condition is imported:

14

\{\begin{array}{l} - \frac{1}{2} m_{p} \frac{d^{2} v}{d x} = \frac{1}{2} (A (x) ρ) v^{2} + S_{s p} S (x) x C_{s} (x) + σ_{c} A (x) C_{s} (x) \\ + 2 X_{t} ε_{f} {(r + (h - x_{0}) t a n α)}^{2} t a n β C_{r} (x), \\ v (0) = v_{0} . \end{array}

Here the velocity and the displacement are converted to dimensionless variables:

15

v^{*} = \frac{v}{v_{0}}, x^{*} = \frac{x}{h} .

By defining a variable $y^{*} = v^{*^{2}}$ , Eq. (14) leads to:

16

\{\begin{array}{l} - \frac{d y^{*}}{d x^{*}} = \frac{π r^{2} h ρ}{m_{p}} y^{*} + \frac{4 S_{s p} π r h^{2}}{m_{p} v_{0}^{2}} C_{s} (h x^{*}) x^{*} + \frac{2 π r^{2} h σ_{c}}{m_{p} v_{0}^{2}} C_{s} (h x^{*}) \\ + \frac{4 X_{t} ε_{f} r^{2} h}{m_{p} {v_{0}}^{2}} {(1 + (\frac{h}{r} x^{*} - \frac{x_{0}}{r}) t a n α)}^{2} t a n β C_{r} (h x^{*}), \\ y^{*} (0) = 1 . \end{array}

To simplify the process of finding solution, the relative importance of every energy absorption mechanisms are estimated firstly. Then, inconsequential factors can be found and ignored.

The characteristic values of different variables involved are showed in Table 1.

Some variables are defined as a function of the impact velocity to estimate the relative importance of the terms that appear in the equation:

17

\{\begin{array}{l} R_{m} = \frac{π r^{2} h ρ}{m_{p}} - 1 0^{- 2}, \\ R_{s p} = \frac{4 S_{s p} π r h^{2}}{m_{p} v_{0}^{2}} - \frac{1 0^{3}}{v_{0}^{2}}, \\ R_{c} = \frac{2 π r^{2} h σ_{c}}{m_{p} v_{0}^{2}} - \frac{1 0^{3}}{v_{0}^{2}}, \\ R_{f} = \frac{4 X_{t} ε_{f} r^{2} h}{m_{p} v_{0}^{2}} - \frac{10}{v_{0}^{2}} . \end{array}

Obviously, the value of $R_{f}$ is very small. Within the velocity range considered, $R_{f}$ is always lower than the others. The energy of tensile fiber failure is ignored to simplify the model as following:

18

\{\begin{array}{l} - \frac{d y^{*}}{d x^{*}} = \frac{π r^{2} h ρ}{m_{p}} y^{*} + \frac{4 S_{s p} π r h^{2}}{m_{p} v_{0}^{2}} C_{s} (h x^{*}) x^{*} + \frac{2 π r^{2} h σ_{c}}{m_{p} v_{0}^{2}} C_{s} (h x^{*}), \\ y^{*} (0) = 1 . \end{array}

The equation can be numerically solved to find the solution:

19

y^{*} = \{\begin{array}{l} - \frac{4 S_{s p} h}{v_{0}^{2} r ρ} x^{*} + \frac{4 S_{s p} m_{p}}{v_{0}^{2} π r^{3} ρ^{2}} - \frac{2 σ_{c}}{v_{0}^{2} ρ} + e^{- \frac{π r^{2} h ρ}{m_{p}} x^{*}} (- \frac{4 S_{s p} m_{p}}{v_{0}^{2} π r^{3} ρ^{2}} + \frac{2 σ_{c}}{v_{0}^{2} ρ} + 1), 0 < x^{*} < x_{0}^{*}, \\ - \frac{4 S_{s p} h}{v_{0}^{2} r ρ} x_{0}^{*} + \frac{4 S_{s p} m_{p}}{v_{0}^{2} π r^{3} ρ^{2}} - \frac{2 σ_{c}}{v_{0}^{2} ρ} + e^{- \frac{π r^{2} h ρ}{m_{p}} x_{0}^{*}} (- \frac{4 S_{s p} m_{p}}{v_{0}^{2} π r^{3} ρ^{2}} + \frac{2 σ_{c}}{v_{0}^{2} ρ} + 1), x^{*} \geq x_{0}^{*} . \end{array}

$x_{0}^{*}$ can be obtained from following equation:

20

\int_{0}^{x_{0}^{*}} \frac{v_{0}}{\sqrt{y^{*} (x^{*})}} d x^{*} = \frac{2 h}{\sqrt{E_{3} / ρ}} .

The expression for residual velocity is obtained, which is given by:

21

v_{r} = \underset{x^{*} \to \infty}{l i m} v (x^{*}) = \sqrt{- \frac{4 S_{s p} h}{r ρ} x_{0}^{*} + \frac{4 S_{s p} m_{p}}{π r^{3} ρ^{2}} - \frac{2 σ_{c}}{ρ} + e^{- \frac{π r^{2} h ρ}{m_{p}} x_{0}^{*}} (- \frac{4 S_{s p} m_{p}}{π r^{3} ρ^{2}} + \frac{2 σ_{c}}{ρ} + v_{0}^{2})} .

For ballistic limit $v_{50}$ , $v_{r} =$ 0, so ballistic limit $v_{50}$ can be expressed by:

22

v_{50} = \sqrt{\frac{\frac{4 S_{s p} h}{r ρ} x_{0}^{*} - \frac{4 S_{s p} m_{p}}{π r^{3} ρ^{2}} + \frac{2 σ_{c}}{ρ} - e^{- \frac{π r^{2} h ρ}{m_{p}} x_{0}^{*}} (- \frac{4 S_{s p} m_{p}}{π r^{3} ρ^{2}} + \frac{2 σ_{c}}{ρ})}{e^{- \frac{π r^{2} h ρ}{m_{p}} x_{0}^{*}}}} .

Table 1Characteristic values of different variables

Variable	Characteristic values
$h$ [m]	10^-3
$r$ [m]	10^-3
$m_{p}$ [kg]	10^-3
$ρ$ [kg/m³]	10³
$X_{t}$ [N/m²]	10⁹
$σ_{c}$ [N/m²]	10⁸
$S_{s p}$ [N/m²]	10⁸
$ε_{f}$	10^-2

4. Model validation and discussion

To validate the analytical model above, analytical results are calculated to compare with experimental result [13]. Here cylindrical projectiles with a diameter of 7.62 mm and a mass of 5.2 g are used to impact 0°/90° layup Kevlar laminates with thickness of 5 mm and 10 mm respectively. The mechanical properties of Kevlar composite are shown in Table 2.

The projectile residual velocities obtained from different laminate thickness values and projectile initial velocities are shown as Fig. 2. It is clear that the differences between results of calculation and experiment reduce as the initial velocity increases for laminates. For laminate with thickness of 5 mm, the error is about 13 % while the initial velocity below 400 m/s, and the error is less than 9 % while the initial velocity over 400 m/s. It shows that the calculated result is closer to experimental result for laminates with thickness of 10 mm than that of 5 mm. Also, good result was found in the residual velocity estimated by the mentioned method [19], but its error is larger than that found by the proposed model.

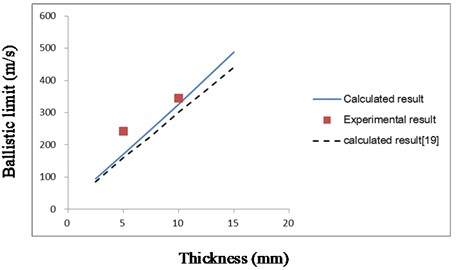
The ballistic limit obtained for different laminate thickness values are shown as Fig. 3.

It is clear that the difference between calculated result and experimental result is larger while the laminates with thickness of 5 mm than which of 10 mm. The ballistic limit of calculated result [19] is lower than that of proposed model.

Table 2Mechanical properties of Kevlar composites

Mechanical property	Value
$ρ$ [kg/m³]	1440
Modulus in $x$ direction $E_{x}$ [GPa]	21
Modulus in $y$ direction $E_{y}$ [GPa]	21
Modulus in $z$ direction $E_{z}$ [GPa]	4.6
Shear modulus in $x y$ direction $G_{x y}$ [GPa]	5.2
$X_{t}$ [MPa]	800
$S_{s p}$ [MPa]	183
$σ_{c}$ [MPa]	80
$ε_{f}$	0.02

Fig. 2Comparison of residual velocities obtained from analysis and experiment for different projectile initial velocities

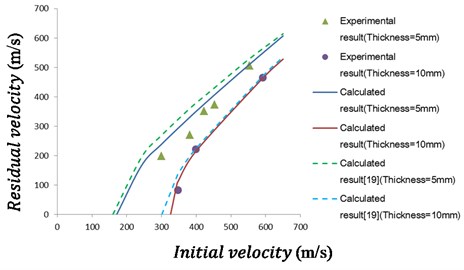
Fig. 3Comparison of ballistic limit obtained from analysis and experiment for different laminate thickness

The key of explaining the error is analyzing the perturbation caused by tensile fiber failure. It is also important to analyze the influence of the energy absorbed by other three different mechanisms. To simplify the process of analysis and estimate the influence of every mechanisms quickly, three dimensionless variables $R_{s p} / R_{f}$ , $R_{m} / R_{f}$ and $R_{c} / R_{f}$ are built.

Fig. 4 shows that the perturbation caused by tensile fiber failure descends as soon as the initial velocity increases. Shear plugging is always the main absorbing energy mechanism (within the velocity range considered). At initial velocity below 370 m/s, the crushing is more important than the momentum transfer. At initial velocity below 100 m/s, the momentum transfer is almost without influence. As the impact velocity increases, the ratio of $R_{m} / R_{f}$ rises quickly. The reason is that the ratio is proportional to square of the projectile velocity. It means that the influence of shear plugging descends as the initial velocity increases, so the solutions between the proposed model and method [19] become closer in Fig. 2.

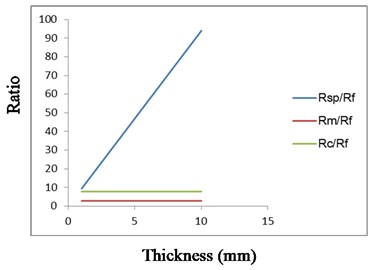
Fig. 5 shows that the perturbation caused by tensile fiber failure descends as soon as the thickness of laminate increases. Shear plugging is the main absorbing energy mechanism while thickness over 1mm. Crushing is always more important than momentum transfer. As the impact velocity increases, the ratio of $R_{s p} / R_{f}$ rises quickly. The reason is that the ratio is proportional to the thickness of laminate. It means that the influence of shear plugging rises as the initial velocity increases, so the solutions between the proposed model and method [19] become larger in Fig. 3.

Fig. 4Ratio of different factor for different projectile initial velocities (thickness = 5 mm)

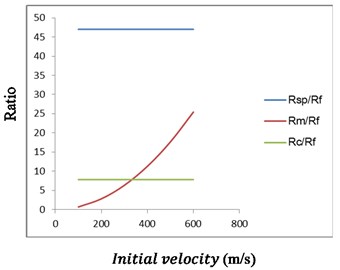
Fig. 5Ratio of different factor for different laminate thickness (v0= 200 m/s)

5. Conclusions

An analytical model to predict residual velocity and ballistic limit after high velocity impact on woven Kevlar laminates is proposed. Four different energy absorption mechanisms for the laminate are considered in the model. Then, the model is simplified to obtain the residual velocity and ballistic limit. The analytical result is calculated to compare with that of experiment. The comparison shows a good correlation between the results obtained both numerically and experimental. The perturbation caused by tensile fiber failure descends as soon as the initial velocity or the thickness of laminate increases. The importance of energy absorbing by shear plugging, crushing and the momentum transfer will change by changing of initial velocity of projectile and thickness of laminate. The method of simplification could be useful in preliminary assessment of engineering.

References

Bhatnagar A. Lightweight Ballistic Composites Military and Law-Enforcement Applications. Abington Hall, Abington, Cambridge, 2006, p. 364-397.

Publisher
Grujicic M., Arakere G. A ballistic material model for cross-plied unidirectional ultra-high molecular-weight polyethylene fibre-reinforced armor-grade composites. Materials Science and Engineering, Vol. 498, 2008, p. 231-241.

Publisher
Nilakantan G., Keefe M., Gillespie Jr J., Bogetti T. Novel multi-scale modeling of woven fabric composites for use in impact studies. 10th International LSDYNA users conference, Dearborn, Michigan, USA, 2008.

Search CrossRef
Zhu G., Goldsmith Dharan W. C. H. K. Penetration of laminated Kevlar by projectiles-II, analytical model. International Journal of Solids and Structures, Vol. 29, Issue 4, 1992, p. 421-436.

Publisher
Sun C. T., Potti S. V. A simple model to predict residual velocity of thick composite laminates subjected to high velocity impact. International Journal of Impact Engineering, Vol. 18, Issue 3, 1996, p. 339-353.

Publisher
Wen H. M. Predicting the penetration and perforation of FRP laminates struck normally by projectiles with different nose shapes. Composite Structures, Vol. 49, Issue 3, 2000, p. 321-329.

Publisher
Wen H. M. Penetration and perforation of thick FRP laminates. Composites Science and Technology, Vol. 61, 2001, p. 1163-1172.

Publisher
Naik N. K., Shrirao P. Composite structures under ballistic impact. Composite Structures, Vol. 66, Issues 1-4, 2004, p. 579-590.

Publisher
Xuan Haijun, Zhang Na Impact response and damage evolution of triaxial braided carbon/epoxy composites. Part I: Ballistic impact testing. Textile Research Journal, Vol. 83, Issue 16, 2013, p. 1703-1716.

Publisher
Ganesh Babu M., Velmurugan Gupta R. N. K. Energy absorption and ballistic limit of targets struck by heavy projectile. Latin American Journal of Solids and Structures, Vol. 3, Issue 1, 2006, p. 21-39.

Search CrossRef
Sikarwar R. S., Velmurugan R., Madhu V. Experimental and analytical study of high velocity impact on Kevlar/Epoxy composite plates. Central European Journal of Engineering, Vol. 2, Issue 4, 2012, p. 638-650.

Publisher
Sikarwar R. S., Velmurugan R. Ballistic impact on glass/epoxy composite laminates. Defense Science Journal, Vol. 64, Issue 4, 2014, p. 393-399.

Publisher
Wang Y. B., Wang X. J., Hu X. Z., Wang F. Experimental study of ballistic resistance of Kevlar laminates. Engineering Mechanics, Vol. 22, Issue 3, 2005, p. 76-81.

Search CrossRef
Wang Y. B., Wang X. J., Bian L., Yu Y. M. CDM model and its application to numerical simulation on fiber-reinforced laminate under penetration. Explosion and Shock Wave, Vol. 28, Issue 2, 2008, p. 172-177.

Search CrossRef
Yahaya R., Sapuan S. M., Jawaid M., Leman Z., Zainudin E. S. Investigating ballistic impact properties of woven kenaf-aramid hybrid composites. Fibers and Polymers, Vol. 17, Issue 2, 2016, p. 275-281.

Publisher
Gu Xingjin, Xu Xiwu, Huang Jing High velocity impact damage of thin composite laminates. Journal of Nanjing University of Aeronautics and Astronautics, Vol. 40, Issue 3, 2008, p. 370-375.

Search CrossRef
Michele Pasquali, Consuelo Terra, Paolo Gaudenzi Analytical modeling of high-velocity impacts on thin woven fabric composite targets. Composite Structure, Vol. 131, 2015, p. 951-965.

Publisher
Chen Z., Yang G., Zhang C., Wang W. Experimental and modeling study on ballistic impact behavior of a woven carbon/epoxy composite. American Society for Composites Thirty-First Technical Conference, 2016.

Search CrossRef
Lopez Puente J., Zaera R., Navarro C. An analytical model for high velocity impacts on thin CFRPs woven laminated plates. International Journal of Solids and Structures, Vol. 44, 2007, p. 2837-2851.

Search CrossRef
Lopez Puente J., Zaera R., Navarro C. Analytical model for high velocity impaction thin CFRPs woven laminated targets. International Journal of Solids and Structures, 2007, p. 1-15.

Publisher
Naik N. K., Shrirao P., Reddy B. C. K. Ballistic impact behavior of woven fabric composites: formulation. International Journal of Impact Engineering, Vol. 32, 2006, p. 1521-1552.

Publisher
Naik N. K., Doshi A. V. Ballistic impact behavior of thick composites: parametric studies. Composite Structures, Vol. 82, 2008, p. 447-464.

Publisher
Brenda Buitrago L., Shirley Garcia Castillo K., Enrique Barbreo Influence of shear plugging in the energy absorbed by thin carbon-fibre laminates subjected to high-velocity impacts. Composites Part B: Engineering, Vol. 49, 2013, p. 86-92.

Publisher

Cited by

A novel simplified ballistic impact theory for woven composites

Ugur Dogan | Emin Sunbuloglu

(2023)

Numerical simulation of armor materials and optimization using gray relational analysis

Caio Lopes Martins Marques | Shiv Ranjan Kumar | Chandramani Goswami | Rahul Verma

(2020)

About this article

Received

08 October 2017

Accepted

27 October 2017

Published

31 December 2017

DOI

https://doi.org/10.21595/jme.2017.19253

Keywords

high velocity impacts

composite laminates

residual velocity

ballistic limit

Acknowledgements

This research is partially supported by the National Natural Science Foundation of China (Grant No. 51475228), the Research Fund of State Key Laboratory of Mechanics and Control of Mechanical Structures (Nanjing University of Aeronautics and Astronautics) (Grant No. MCMS-0517K01) and the Priority Academic Program Development of Jiangsu Higher Education Institutions. The authors wish to thank Mr. Peng Haifeng, Mr. Wushuo and Mr. Li Jin of Chrdi (China) for their technical and financial support. Special thanks also to Mr. Jin Wanzeng and Mr. Mengxiangji for useful discussions.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 05 18

Evaluation of failure criteria for residual tensile strength of composite laminates with circular holes

Botao Hu, Xiangming Chen, Fanchen Deng, Xiaobo Sun

Research article

2022 06 30

Parametric studies on SEA parameters for coupled plates made of composite laminate

Sridhar N Shastry, Subrahmanya S Swamy

Research article

2021 03 25

Experimental and numerical investigation on the impact resistance of fiber metal laminates

Chang Liu, Guo Lai Yang, Yue Xiao, Quanzhao Sun

Research article

2019 04 25

Modal analysis of sandwich panel with composite laminated faces

Eva Kormanikova

C. Fangyu, Z. Li, T. Yihao, and Z. Xiaoming, “An analytical modeling for high-velocity impacts on woven Kevlar composite laminates,” Journal of Measurements in Engineering, Vol. 5, No. 4, pp. 249–256, Dec. 2017, https://doi.org/10.21595/jme.2017.19253

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jme.2017.19253
UR  - https://doi.org/10.21595/jme.2017.19253
TI  - An analytical modeling for high-velocity impacts on woven Kevlar composite laminates
T2  - Journal of Measurements in Engineering
AU  - Li, Zhou
AU  - Fangyu, Chen
AU  - Yihao, Tang
AU  - Xiaoming, Zhou
PY  - 2017
DA  - 2017/12/31
PB  - JVE International Ltd.
SP  - 249-256
IS  - 4
VL  - 5
SN  - 2335-2124
SN  - 2424-4635
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2017,
	doi = {10.21595/jme.2017.19253},
	url = {https://doi.org/10.21595/jme.2017.19253},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {5},
	number = {4},
	pages = {249--256},
	author = {Zhou Li and Chen Fangyu and Tang Yihao and Zhou Xiaoming},
	title = {An analytical modeling for high-velocity impacts on woven Kevlar composite laminates},
	journal = {Journal of Measurements in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Li, C. Fangyu, T. Yihao, and Z. Xiaoming, “An analytical modeling for high-velocity impacts on woven Kevlar composite laminates,” Journal of Measurements in Engineering, vol. 5, no. 4, pp. 249–256, Dec. 2017, doi: 10.21595/jme.2017.19253.

Copy IEEE

Copied to clipboard!

Li, Zhou, Chen Fangyu, Tang Yihao, and Zhou Xiaoming. “An Analytical Modeling for High-Velocity Impacts on Woven Kevlar Composite Laminates.” Journal of Measurements in Engineering 5, no. 4 (December 31, 2017): 249–56. https://doi.org/10.21595/jme.2017.19253.

Copy Chicago

Copied to clipboard!

An analytical modeling for high-velocity impacts on woven Kevlar composite laminates

Abstract

1. Introduction

2. Analytical model

3. Model simplification

4. Model validation and discussion

5. Conclusions

References

Cited by

About this article

Related Articles