Analytic study on the foundation of shaker based on AIR spring

1. Introduction

The foundation is an important part of the electro-dynamic vibration system. The reaction displacement of the foundation under vibration directly affects the performance of the shaker and the accuracy of the test. At present, the solid-foundation with vibration isolation groove is mostly adopted. The foundation is separated from the surrounding soil by the vibration isolation groove, which weakens the transmission of vibration and reduces the influence on the surrounding environment. With the development of society and the progress of industrial technology, it is necessary and possible that the shaker is installed on the floor. Then, the static-bearing capacity of floor and the dynamic characteristics of the system must be taken into account in the design of the foundation [1-3].

In recent years, the low-frequency Air spring vibration isolation device, with high control accuracy and high pay-load, were widely used in large equipment installation, and better than the traditional vibration isolation device. The structural response under dynamic-loading is expressed mainly by displacement. Then, the maximum displacement response is the fundamental index for the design of vibration isolation layer and the response of superstructure.

2. Dynamic model of shaker and vibration isolation system

The principle of electro-dynamic vibration system is that the moving is produced by the magnetic force acts on the electric conductor. As Fig. 1 shown, the moving system is composed of armature frame, armature, connecting rod, supporting spring and test table. When the frequency is low, test table and armature can be regarded as rigid connection. The support spring has sufficient rigidity to support the entire system (including load), its stiffness is constant within the range of the force possible, which guarantee the shaker has stable characteristics in its nominal frequency range. The vibration force will transfer to the installation foundation by the support. So, it is necessary to take vibration isolation settings between shaker and bracket, between bracket and installation foundation. Fig. 2 shows a typical trunnion-vibration isolation system, which springs ware placed between shaker and bracket.

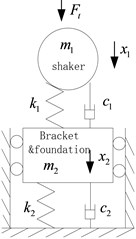
In order to study the relationship between shaker and vibration isolation foundation, it is simplified to two-degree-of-freedom system, as shown in Fig. 3. $m_1$ represents the quality of shaker(including electric coil); $m_2$ represents the quality of the bracket and the foundation; $k_1$ and $c_1$ respectively represent the stiffness and damping coefficient of the trunnion-vibration isolation system; $k_2$ and $c_2$ respectively represent the stiffness and damping coefficient of the foundation-vibration isolation system; $F_t=F_0\sin \omega t$ represent the reaction dynamic load acted on the system; $x_1$ and $x_2$ respectively represent the displacement of shaker and foundation for time $t$. Then the dynamic equilibrium equation of the system is:

The steady-state response of the system is considered only, and the solution of equation (1) can be expressed as:

Substituting Eq. (2) into Eq. (1) yields:

where ${\omega }_1$and ${\omega }_2$ defined as follows: ${\omega }_1=2\pi f_1=\sqrt{k_1/m_1}$, ${\omega }_2=2\pi f_2=\sqrt{k_2/m_2}$.

The principle of vibration test is by using the sensor to test the real-time acceleration signal of the table and adjusting the output of the power amplifier. If the displacement of foundation becomes greater, then it will affect the accuracy of vibration control and the safety of test. Therefore, it is necessary to design a vibration-isolation-foundation.

Fig. 1The principle of vibration system

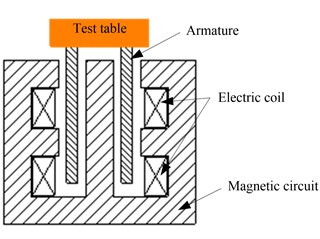
Fig. 2Trunnion-vibration isolation system

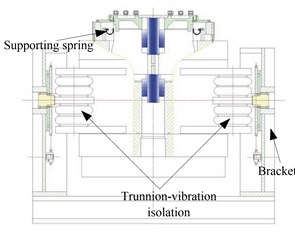
Fig. 3The dynamics model of vibration isolation system

3. Design of vibration isolation system

3.2. Vibration isolation transfer function

In order to analysis the performance of the foundation-vibration isolation system accurately, the mechanical model, as shown in Fig. 1, is simplified to one-degree-freedom system, composed of the shaker system and the foundation-vibration isolation system. Then, the vibration transmission obtained, it can be expressed as the ratio of the acceleration response of the isolation foundation to the input acceleration, with $\zeta =c_2/2\pi$ the damping ratio [4]:

9

$R_a=\frac{{\ddot{x}}_2}{{\ddot{x}}_1}=\sqrt{\frac{1+{\left(2\zeta \omega /{\omega }_2\right)}^2}{{\left[1-{\left(\omega /{\omega }_2\right)}^2\right]}^2+{\left(2\zeta \omega /{\omega }_2\right)}^2}}.$

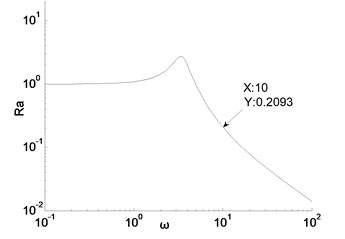
The relationship between the vibration isolation rate $R_a$ and $\zeta$, $\omega /{\omega }_2$ are shown in Fig. 3. When the damping ratio is constant, the vibration isolation rate is only related to the forced frequency. As the forced frequency approaches the nature frequency of the isolation system, the vibration isolation rate becomes greater. When $R_a>$ 1, which represents that the vibration is amplified. In actual use, the vibration isolation system should be rationally designed, so as to avoid the amplification area, as shown in Fig. 4.

Taking ${\omega }_2=$ 3.5, $\zeta =$ 0.2 as example, When the frequency $\omega =$ 10, the vibration isolation rate $R_a=$ 0.2093, the result reveals that the vibration transmission was reduced by 80 %; and the vibration rapidly attenuates with the increase of frequency, as shown in Fig. 5.

Fig. 4Relationship between Ra and ω/ω2

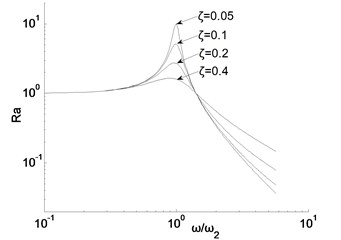
Fig. 5The example with ω2= 3.5, ζ= 0.2

4. Frequency response analysis of vibration isolation system

The reaction force passes through the trunnion and foundation vibration isolation system. Then, the residual dynamic load causes the displacement of the foundation as shown in Eq. (4). According to Eq. (4), the displacement response of the foundation is inversely proportional to $m_1$ and $m_2$. On condation of $m_1$ fixed, the foundation displacement response becomes smaller, as the greater of $m_2$. In the traditional shaker installation, the quality of foundation is required about 50 times of the maximum exciting-force.

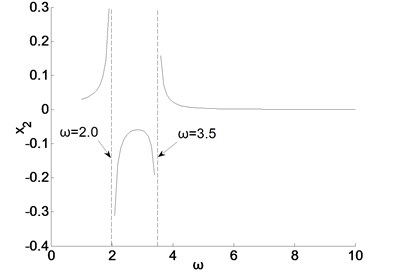
In order to easy analysis, Table 1 lists the example of the shaker structure and the AIR-spring vibration isolation system parameters. The relationship between frequency response and vibration isolation foundation and shaker structural parameters were analysed, the results were shown in Fig. 6. As can be seen from the coordinate chart, there are two breakpoints; When $\omega$ tends to ${\omega }_1$, ${\omega }_2$, the displacement of foundation tends to infinity. Combining the Eq. (10) analysis, the stiffness $k_1$ and $k_2$ affects the frequency of the first and second breakpoint, and the mass $m_1$ and $m_2$ has an influence on the resonance frequency and the amplitude in all bands.

Fig. 6Function graphs between frequency response and nature frequency

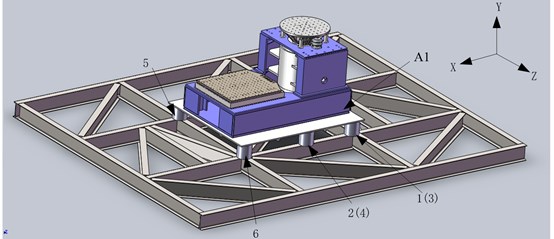
5. Test verification

According to the above analysis, the vibration isolation foundation of one-10T’s shaker is designed, as shown in Fig. 7. In order to improve the static bearing capacity of floor, I-beam sub-truss was adopted, placed on the bearing beam of building. The height of I-beam is 320 mm, the weight of each meter is 57.74 kg, and the total weight of the support-frame is 5.3 tons. The support-plate was installed on the bottom of the shaker, in order to realize the transfer between AIR-spring and the shaker. The material adopts carbon-steel, and the weight is 2.1 tons, and the size is 2.8 m×3.2 m, and the thickness is 20 mm. The bottom of support-plate was set stiffeners, with thickness 25 mm and height 130 mm.

Between the support plate and the sub-truss, there are 6 sets of 380150J-1 Air springs, which were provided by Chenguang Rubber Company, in order to achieve the isolation effect. The foundation isolation system is designed with two pressure regulator, and No. 1 pressure regulator is responsible for controlling the pressure of the 1#~4# Air spring, and the No. 2 pressure regulator is responsible for controlling the pressure of the 5#~6# Air spring. In actual use, the pressure can be adjusted according to the bearing capacity and frequency range to achieve the required natural frequency.

Fig. 7The vibration isolation system of 10T’s shaker

To verify the influence of vibration frequency of system frequency response, the vibration table bearing corner paste three to A1 acceleration sensor, three direction measurement test in the process of acceleration response, Based on empirical formula: $\ddot{x}=x{f}^{2}g/250$, we can calculate the displacement. Table 2 shows the test condition.

Fig. 8The acceleration of horizontal (X) direction

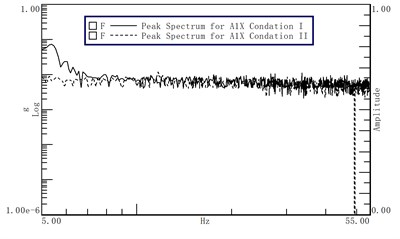
Fig. 9The acceleration of vertical (Y) direction

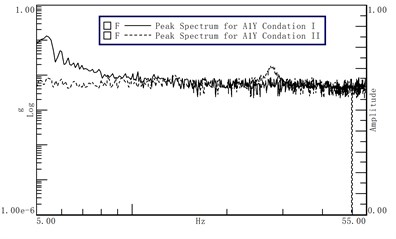
Fig. 10The acceleration of horizontal (Z) direction

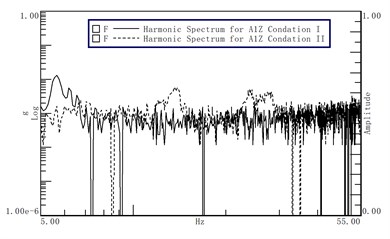
According to the data measured shown in Figs. 8-10, the following conclusions can be drawn:

1) When the vibration frequency is $\omega ={\omega }_2=$5.37 Hz, the maximum accelerations of the three corners of the bracket are ${\ddot{x}}_x=$ 0.1 g, ${\ddot{x}}_y=$ 0.13 g and ${\ddot{x}}_z=$ 0.07 g respectively. Then, the maximum displacement (peak to peak) in three directions are available: $x_x=$ 1.73 mm, $x_y=$ 2.25 mm, $x_z=$ 1.21 mm;

2) Adjust the air spring pressure, you can avoid the amplification area, to achieve the desired the optimum isolation efficiency and displacement response;

3) The nature frequency of the air spring is proportional to the pressure of the Air spring, and the nature frequency of the system can be increased by increasing the charging pressure.

6. Conclusions

In this paper, the dynamic analysis model is established according to the structural characteristics of the electro-dynamic shaker. In accordance with the demand, the design and analysis of the basic isolation scheme are carried out, and the vibration isolation scheme based on the air spring is put forward. The vibration isolation performance of a 10-ton vibration platform is measured and analyzed. The scheme has broken through the difficulty of placing large vibration table in the floor structure, and has carried out theoretical research and practical verification to develop a new installation environment of the vibration table. The practical engineering application results show that increasing the quality of supporting plate or adjusting system damping can effectively control the vibration displacement of installation foundation and improve the stability of the system.