Characteristic analysis of vibration isolation system based on high-static-low-dynamic stiffness

2.1. Description of general model

The system depicted in Fig. 1 is a parallel connection of two oblique linear springs with identical stiffness $k_1$ and a vertical linear spring with identical stiffness $k_2$. The oblique springs are hinged at $A$ and $B$, and connected with the vertical spring at point $C$. The configuration geometry is decided by horizontal distance $a$ from point $A$ to $C$ and initial height $h$, while $x$ denotes the vertical displacement from the initial unloaded position caused by the force $f$.

Fig. 1Schematic representation of isolator based on HSLDS

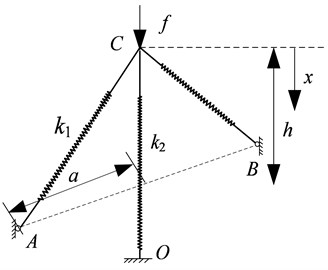
a)

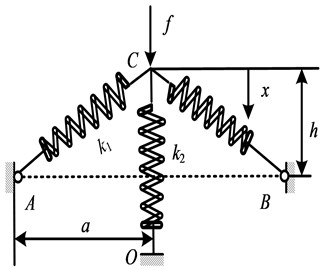
b)

The general equation between the force $f$ and the displacement $x$ can be derived as:

Noting that$y=x-h$, Eq. (1) can be remade in the dimensionless form as:

where ${\widehat{k}}_1=k_1/k_2$, $\widehat{y}=y/\sqrt{a^2+h^2}$, $\widehat{f}=f/\left(k_2\sqrt{a^2+h^2}\right)$, $\widehat{a}=a/\sqrt{a^2+h^2}$. Approximating Eq. (2) to the third order by using the Maclaurin series expansion, one yields:

The dimensionless dynamic stiffness can be obtained by differentiating Eq. (3) to $\widehat{y}$:

The dimensional form of Eq. (4) is $k=k_2-2k_1(1-1/\widehat{a})+(3k_1{a}^2/\widehat{a})y^2$. It is clear that the oblique springs can reduce the positive stiffness so that the linear natural frequency is smaller in the isolation range; and they introduce the cubic stiffness term so that the peak response bends to higher frequencies, what potentially reduces the frequency region.

The SDOF system is depicted in Fig. 2. It includes a rigid mass $m$ suspended on a three-springs mount in parallel with a viscous damper$c$excited by harmonic excitation $f_e=F\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{\Omega }T$. The mass moves in the vertical direction through the guide rod and bushing. By applying the Newton’s second law, the motion equation of SDOF system can be expressed as.

where ${k\text{'}}_1=k_2+2k_1\left(1-1/\widehat{a}\right)\text{,}$${k\text{'}}_3=3k_1{a}^2/\widehat{a}$ and $(\cdot )\text{'}=d(\cdot )/dt\text{.}$ The following dimensionless variables are introduced as $t={\mathrm{\Omega }}_{n}T$, $\omega =\mathrm{\Omega }/{\mathrm{\Omega }}_n$, ${\mathrm{\Omega }}_n=\sqrt{{k\text{'}}_1/m}$, $\xi =c/\left(m{\mathrm{\Omega }}_n\right)$, $f=F\sqrt{{k\text{'}}_3/{{k\text{'}}_1}^3}$. Eq. (5) can be expressed in the dimensionless form as:

What is a hardening Helmholtz-Duffing oscillator and primes.

Fig. 2Structural model of SDOF system with HSLDS characteristic: 1 – loading platform, 2 – oblique spring, 3 – guide device, 4 – pillar, 5 – vertical spring, 6 – base plate, 7 – linear bearing, 8 – sliding rod

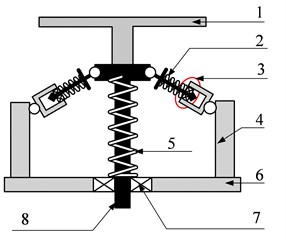
a)

b)

2.2. Amplitude-frequency equation and stability analysis

Considering that the vibration isolation system with the HSLDS characteristic is a strongly nonlinear, the Mathieu equation criterion and perturbation methods are invalid. The corresponding steady-state approximate solution is obtained by using the general Hill equation and HBM [11].

Applying the HBM, the solution of Eq. 6, denoted by $\widehat{u}$, is supposed as a truncated Fourier series $u_0$ plus a small perturbation$v$. The system response is given by:

where $r_0$, $r_i$ and ${\varphi }_i$ are Fourier parameters of harmonic balance solution and $N$ is the truncated order. In particular, substituting Eq. (7) into Eq. (6) with $N=$ 3, Eq. (6) can be transferred as:

where the functional dependence of $P_0$, $P_k$, $G_k$, ${\theta }_0$, ${\theta }_{jc}$ and ${\theta }_{js}$ on the parameters $r_0$, $r_i$, ${\varphi }_i$ is shown in Appendix. Since the substitution introduced seven parameters into the system, which can be obtained by the coefficients $P_j(r_0,r_i,{\varphi }_i)$ and $G_j(r_0,r_i,{\varphi }_i)$ of harmonic $\mathrm{c}\mathrm{o}\mathrm{s}\left(k\omega t\right)$ and $\mathrm{s}\mathrm{i}\mathrm{n}\left(k\omega t\right)$ equated to zero respectively ($i=$ 1,…, 3, $j=$ 1,…, 9, $k=$ 1,…, 9). The linearized variational equation of the Eq. (8) can be written as:

It is worthy of noting that the stability analysis of Eq. (7) is changed to the general Hill equation. According to the Floquet theory [12], the solution of Eq. (10) can be assumed to be:

where $\sigma$ is the characteristic Floquet exponent. Eq. (10) is substituted into Eq. (9), and the coefficients of the same harmonics are equated and ignore the higher harmonics. This leads to an infinite set of linear homogeneous equations$\mathbf{A}\mathbf{x}=$ 0, where $\mathbf{x}$ is the column vectors $(\cdots ,b_i,b_{i+1},\cdots {)}^T$, $\mathbf{A}$ is the matrix of coefficients. Following the procedure stated in Ref. [12], $\mathbf{A}\mathbf{x}=$ 0 exists an nontrivial solutions if the determinant of $\mathbf{A}$, denoted by $\mathrm{\Delta }$, vanishes. Thus, the stable (respectively, unstable) condition is determined by whether $\mathrm{\Delta }(\sigma =0)>0$ is positive (negative), the boundary between the stable and unstable regions is $\mathrm{\Delta }(\sigma =0)=$ 0.

This paper aims to find the primary resonance response. The corresponding steady-state harmonic solution is supposed to be $\widehat{u}=r_0+r_1\mathrm{c}\mathrm{o}\mathrm{s}(\omega t-{\varphi }_1)+v$, which leads to the following amplitude-frequency relation according to the Appendix:

With the term containing ${\varphi }_1$ eliminated, Eq. (11) can be expanded and arranged. The amplitude-frequency equation can be yielded as:

With the term containing $r_1$ eliminated, Eq. (11) can be expanded and arranged. The phase-frequency equation can be yielded as:

The two positive solutions for $\omega$, which are the resonant and non-resonant branches in the frequency response function, can be solved analytically in Eq. (12):

The peak response can be reached when ${\omega }_1$ and ${\omega }_2$ are equal. Thus, the peak response of $r_{1p}$ and corresponding ${\omega }_p$ are found as follows:

Noting that $N=$ 1 and according to the procedure shown in Appendix, Eq. (9) can be written as:

where $p=1+3{r_1}^2/2$, $q=3{r_1}^2/4$, $\phi =\omega t-{\varphi }_1$.

According to the Floquet theory, the solution of Eq. (16) can be assumed to be:

By substituting Eq. (17) into Eq. (16) and applying the HBM, one can conclude that:

With the term containing $\mathrm{s}\mathrm{i}\mathrm{n}\left(3\phi \right)$ and $\mathrm{c}\mathrm{o}\mathrm{s}\left(3\phi \right)$ neglected, the coefficients of harmonics $\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$ and $\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$ are equated to zero respectively, what can be derived as:

Nontrivial solutions exist only when the determinant of the matrix in Eq. (19), denoted by $\mathrm{\Delta }$, vanishes, waht can be derived as:

Eq. (20) is the boundary between the stable and unstable regions and the unstable regions can be determined by $\mathrm{\Delta }<0$.

2.3. Effects on FRCs for damping ratio and excitation amplitude

In this section, the effects of the damping ratio and excitation amplitude on the shape of the FRCs are investigated by the controlling variables method. It is worthy of noting that the steady-state solution is obtained only by considering the component of the primary resonance response, where the classical Runge Kutta method needs to be used to validate the accuracy of the appropriate solutions obtained by HBM. These curves are plotted in Figs. 3-5 for three distinguishable cases, where the red solid line and the blue dotted line of the FRCs represent the stable and unstable solutions, respectively, and the symbols black “o” and green “*” denote the numerical solution and peak response, respectively. It can be observed from the Figs. 3-5, the analytical and numerical results fit in well.

Fig. 3FRCs of system with different damping ratios where f= 0.5 and ξ= 0.1, 0.2, 0.3

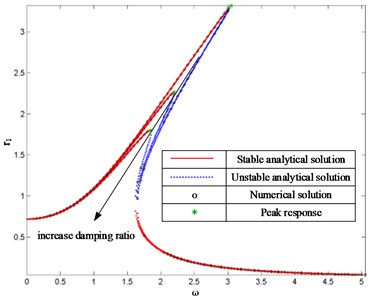
Fig. 4FRCs of system with different excitation amplitudes where ξ= 0.1 and f= 0.5, 1, 1.5

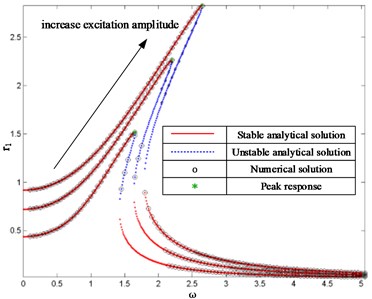
Fig. 5Dependence of response amplitude on excitation amplitude where ξ= 0.1 and ω= 1.6, 2, 2.2

As shown in Fig. 3, an increase in the damping ratio results in a decrease in the resonance frequency and peak response when the excitation amplitude is fixed. The unstable regions also decreases as the damping radio increases and the FRCs approach is equal at lower or high frequencies. The FRCs of the harmonic response are bent to the right, as they are intended for the hardening stiffness characteristic. However, the FRCs will tend to the linear form when the damping ratio is excessive.

In the above analysis, the excitation amplitude of the HSLDS system is always fixed. It is interesting to study the effects of excitation amplitude on the FRCs when the damping ratio is fixed. The FRCs with different excitation amplitudes are plotted in Fig. 4. It can be seen obviously that larger excitation amplitude can result in both larger resonance frequency and peak response. An increase in the excitation amplitude yields an increase in the unstable region. The FRCs changes are larger with larger excitation amplitude at lower frequencies while that approaches are the same at high frequencies.

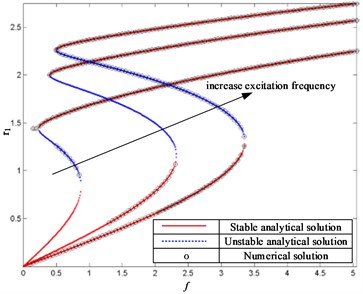
The dependence of the response amplitude on the excitation amplitude is plotted in Fig. 5. By observing Fig. 5, sometimes the number of steady-state solution is only one, sometimes it is three, depending on the initial conditions. The region of existing three stable solutions extends as the excitation frequency increases.

2.4. FT definition

The FT is defined as the ratio between the amplitude of force $f_b$ transmitted to the base and amplitude of the excitation force $f$ [13]:

The $f_b$ contains the elastic force and damping force, which can be expressed by:

Thus, substituting Eq. (12) and Eq. (13) into Eq. (22) and only considering the dynamic force, the FT of the HSLDS isolator can be expressed by:

The peak FT corresponds to the peak response $r_{1p}$. Substituting Eq. (15) into Eq. (23), one yields:

where $\mathrm{\Theta }=\sqrt{{\xi }^6-8{\xi }^4+16{\xi }^2+48f^2}$. For the ELS, the mathematical expression of FT is given in dimensionless quantities by:

2.5. Effects on FT for damping ratio and excitation amplitude

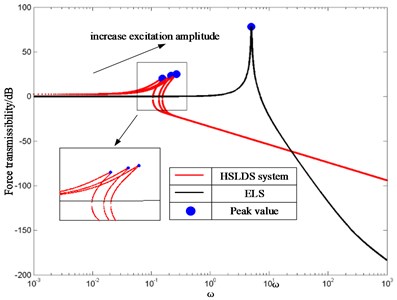
The Effects on the FT of the HSLDS system and the ELS for the damping ratio and excitation value are plotted in Figs. 6-7, where the red solid parts and black solid parts represent the FT of the HSLDS system and the ELS respectively, the symbols “●” denote the peak amplitude of FT, and the FT values are expressed in dB, i.e. as 20 $lo{g}_{10}T$. By inspecting Fig. 6-7, one conclusion can be obtained that the isolation performance of the HSLDS system will be better or worse than that of the ELS depending on the excitation frequency and system parameters.

As shown in Fig. 6, larger damping ratio yields both smaller peak amplitude and smaller resonance frequency of the FT when the excitation amplitude is fixed. However, the excessive damping ratio is detrimental to the isolation performance of HSLDS system at high frequencies. As for the ELS, larger damping ratio yields smaller peak amplitude, while the resonance frequency remains unchanged. As compared with the ELS, the HSLDS system has a smaller initial frequency, wider isolation band and better isolation performance. But when the excitation frequency is excessive, the FT of the HSLDS system is greater than that of the ELS.

As shown in Fig. 7, an increase of the excitation amplitude yields both larger peak value and larger resonance frequency of the FT when the damping ratio is fixed. The FTs of the different excitation amplitudes approach to the same level at higher frequencies. As for the ELS, the peak amplitude and resonance frequency are independent from the excitation amplitude. As compared with the ELS, the HSLDS system has a smaller initial frequency, wider isolation band and better isolation performance; but the excessive excitation frequency will deteriorate the isolation performance of the HSLDS system.

Fig. 6FT of HSLDS system and its ELS with different damping ratios where f= 0.5 and adjusted ξ= 0.1, 0.2, 0.3

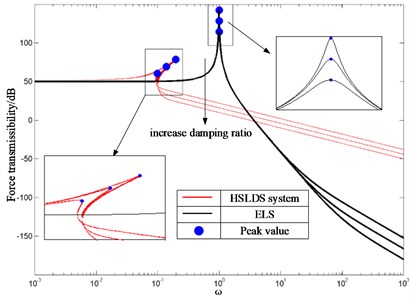
Fig. 7FT of HSLDS system and its ELS with different excitation amplitudes where ξ= 0.1 and f=0.5,1,1.5 0.5, 1, 1.5

2.6. Experimental investigation

To assess the attenuation performance of the proposed SDOF-HSLDS system and to validate the nonlinear phenomenon presented in the previous section, a prototype experiment is carried out. The experimental apparatus of the HSLDS is shown in Fig. 8. The mass is supported by the vertical spring and moves in the vertical direction through the guide rod and bushing. The HSLDS isolator was installed at a rubber vibration isolation system. A vibration exciter powered by a power amplifier is mounted on top of the mass to provide external force in the vertical direction. Between the exciter and the mass, a force sensor is installed to measure the excitation force. Another force sensor is placed underneath the base plate of the HSLDS device to measure the transmitted force during vibration. A data acquisition analyzer is used to extract the output signal from the sensors. A personal computer is used to handle the I/O data operation for the whole measuring system. The experimental setup can be divided into three steps: excitation system, data acquisition system and measured subject. The isolator parameters are shown in Table 1.

The vibration isolation performance is assessed by the FT, which is defined as the ratio of the root mean square (RMS) value of the force transmitted to the base, and as of the RMS value of the excitation force. A linear system is used for a benchmark comparison. The external excitation frequency is varied from 0.5 to 25 Hz. In the actual experiments, two series of experiments are conducted for two series of excitation conditions. The excitation force keeps constant at the level of 20 N for the Case I and keeps constant at the level of 10 N for the Case II. Fig. 9 shows the transmissibility of different levels of excitation force. It is evident that the linear system has the resonance peak of about 2.1 Hz, while the HSLDS system is not involved in the resonance.

Fig. 8Experimental setup of HSLDS isolator

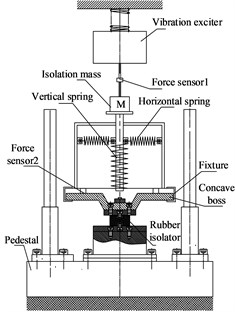
a) Schematic representation of isolator

b) Prototype of experimental apparatus

Fig. 9Experimental comparison of force transmissibility between HSLDS and ELS at different levels of excitation force

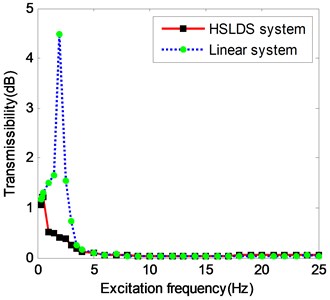
a) Case I

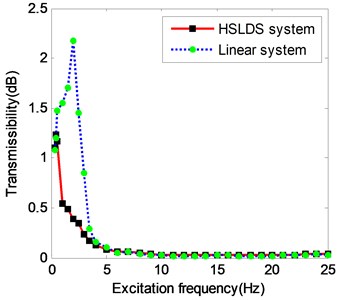
b) Case II

Theoretically, the HSLDS system has a bended resonance peak, but a small damping can make the peak vanish. It is because that the stiffness of the HSLDS system about the equilibrium is close to zero so that the resonance peak has shifted to a lower frequency. The HSLDS system starts the effective attenuation from 0.3 Hz where the transmissibility value is less than one, while the ELS can only start from 3 Hz. The performance of the HSLDS system appears to be equivalent to that of ELS in the high-frequency band after 4 Hz. It can be seen obviously that the performance of the proposed HSLDS system is superior to the ELS in terms of the isolation frequency region, which validates the concept of HSLDS isolator usage to lower the dynamic stiffness to a positive stiffness.

3.1. 2DOF nonlinear isolation system and equivalent linear isolation system

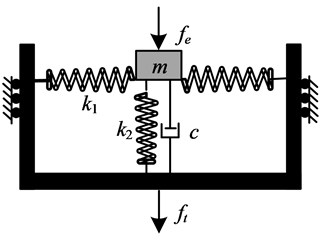
In this section the 2DOF nonlinear (hereinafter referred to as “N-N”) isolation system shown in Fig. 8 is investigated to see if this isolation performance is superior to the corresponding 2DOF linear (hereinafter referred to as “L-L”) isolation system. The N-N isolation system, which includes the mass of vibration object $m_1$, together with a vertical stiffness $k_{21}$, a viscous damper $c_1$ and two horizontal stiffness $k_{11}$; and the mass of the intermediate object $m_2$, in parallel with a vertical stiffness $k_{22}$, a viscous damper $c_2$ and two horizontal stiffness $k_{12}$, consists of two SDOF isolators shown in Fig. 10(a). $f_t$ is the force transmitted to the base, and $f_t$ is the excitation force. $x_1$ and $x_2$ denote the vertical displacement of $m_1$ and $m_2$, respectively.

Fig. 10Schematic of N-N and L-L isolator

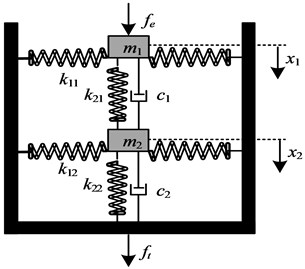
a) N-N configuration

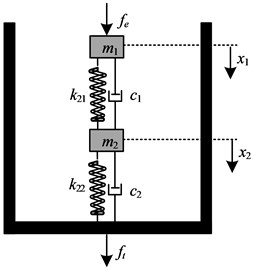
b) L-L configuration

In the analysis above, the motion equation of the SDOF system with the HSLDS characteristic in Fig. 2 can be approximated by:

Thus, the motion equation of the N-N isolation system under harmonic force excitation can be expressed as:

Eq. (27) can be transferred into the matrix form as:

where:

By introducing the dimensionless parameters as follows:

Eq. (28) can get the dimensionless dynamic equation:

where:

By applying the HBM [14-15], set the Eq. (29) solution as:

where $a_{i,n}$, $b_{i,n}$ and $N$ represent the Fourier coefficient of harmonic balance solution and truncated order, respectively. The first and second derivatives of Eq. (30) are given by:

By substituting Eq. (31) into Eq. (29), one can obtain the appearance of high-order ${\widehat{x}}_i\left(t\right)$ term. According to the orthogonally of trigonometric functions [16-17], one can reach:

where:

Supposing that $N=$ 1, the solution of Eq. (29) can be assumed as:

By substituting Eq. (34) into Eq. (29) and setting the coefficients of the terms including $\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)$ and $\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$ to be zero respectively and ignoring the higher harmonics, one yields the implicit amplitude-frequency equation in the form of matrix derived as:

where:

The dimensionless force transmitted to the base is:

where ${\widehat{\mathbf{K}}}_{t1}=\begin{array}{ll}[{\alpha }_1-1& {\alpha }_2-1]\end{array}$, ${\widehat{\mathbf{K}}}_{t3}=[\begin{array}{ll}{\beta }_1& {\beta }_2]\end{array}$, ${\widehat{\mathbf{C}}}_t=\begin{array}{ll}[0& 2{\xi }_2]\end{array}$.

Assuming that ${\widehat{f}}_t={\widehat{F}}_t\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t+{\phi }_T\right)$, the force magnitude can be obtained as:

where ${\mathrm{\Phi }}_T=\left[\begin{array}{ll}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_T& \mathrm{s}\mathrm{i}\mathrm{n}{\phi }_T\end{array}\right]$.

According to the Eq. (21), the FT of the N-N isolator can be expressed by $T_f={\widehat{F}}_t/\widehat{F}$.

For a comparison, two pairs of horizontal springs are removed, and the corresponding linear isolator is shown in Fig. 10(b). The dimensionless dynamic equation for the L-L isolation system can be expressed as:

where:

The dimensionless force transmitted to the base is:

where:

Assuming that ${\widehat{f}}_t={\widehat{F}}_t\mathrm{c}\mathrm{o}\mathrm{s}(\omega t+{\phi }_T)$, the force magnitude can be obtained as:

where ${\mathrm{\Phi }}_T=\left[\begin{array}{ll}\mathrm{c}\mathrm{o}\mathrm{s}{\phi }_T& \mathrm{s}\mathrm{i}\mathrm{n}{\phi }_T\end{array}\right]$.

According to the Eq. (21), the FT of the L-L isolator can be expressed by $T_{fl}={\widehat{F}}_{tl}/\widehat{F}$.

3.2. Effect of parameters on FT

In the above analysis, the FT is closely related to the excitation amplitude, mass ratio and damping ratio. It is interesting to study the effects of different system parameters on the FT with the help of the controlling variable method. The FTs of N-N and L-L isolation system are plotted together to compare the isolation performance, expressed in dB. A given set of parameters ${\alpha }_1=$ –0.02, ${\beta }_1=$ 4.47, ${\alpha }_2=$ 0.98, ${\beta }_2=$ 4.47,$\widehat{k}=$ 1 are chosen to conduct the following investigation.

Fig. 11 shows the FT of N-N isolator and L-L isolator with the changed excitation amplitude. It can be seen that the first and second resonance frequencies and corresponding peak of FTs increase obviously as the excitation amplitude increases. However, the FT of L-L isolator is not affected by the excitation amplitude. The FT of the N-N isolator is larger than that of the L-L isolator at low frequencies while the FT of the N-N isolator changes to a smaller value than that of the L-L isolator at frequencies greater than the first resonance frequency. Thus, one can conclude that the N-N isolator outperforms than that of the L-L isolator at high frequencies.

Fig. 11FT of N-N isolator and L-L isolator with different excitation amplitudes where ξ1=ξ2= 0.03, μ= 2 and f= 0.01, 0.1, 0.5

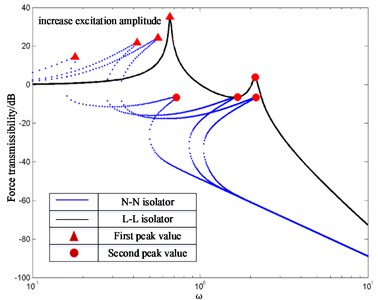
Fig. 12 shows the effect on the FT with the changed mass ratio. For the N-N isolator, it can be seen that an increase of the mass ratio will result in an increase of the first resonance frequency and corresponding peak of FTs, but in a decrease of the second resonance frequency and corresponding peak of FTs. However, for the L-L isolator, one can conclude that the first resonance frequency, corresponding FT peak and the second resonance frequency decrease, while the second peak of FTs increases as the mass ratio increases. Thus, an increase of the mass ratio can broaden the frequency region of isolation, but a decrease of the isolation performance can occur near the second resonance frequency.

In the previous sections, the isolation performance of the N-N isolator is better than the L-L isolator for specific values of damping ratio. Here the effects of the damping ratio on the FT are investigated in Fig. 11 when the excitation amplitude and mass ratio are fixed. Fig.13(a) illustrates that the damping ratio ${\xi }_2$ in the lower stage is fixed and the damping ratio ${\xi }_1$ of the upper stage is varied. By inspecting Fig. 13(a), one can conclude that the first resonance frequency and corresponding peak of the N-N isolator and L-L isolator are hardly changed after the damping ratio${\xi }_1$increased. But the second resonance frequency, corresponding peak of the N-N isolator and second peak of the L-L isolator reduce with the increase of the damping ratio ${\xi }_1$, while the second resonance frequency of the L-L isolator remains unchanged. But an increase of the damping ratio ${\xi }_1$ will deteriorate the isolation performance at frequencies greater than the second resonance frequency. Fig. 13(b) illustrates that the damping ratio ${\xi }_1$ in the upper stage is fixed, the damping ratio ${\xi }_2$ of the lower stage is varied. By inspecting Fig. 13(a), one can conclude that the first resonance frequency, corresponding peak and second resonance frequency of the N-N isolator decrease as the damping ratio ${\xi }_2$ increases, while the second peak increases. The first resonance frequency and corresponding peak of the L-L isolator decrease as the damping ratio ${\xi }_2$ increases, while the second resonance frequency and corresponding peak remain unchanged. Thus, it is preferable to have properly high damping ratio ${\xi }_1$ to control the response at the second resonance frequency and as a small damping ratio ${\xi }_2$ to reduce the transmitted force.

Fig. 12FT of N-N isolator and L-L isolator with different mass ratios where ξ1=ξ2= 0.03, f= 0.1 and μ= 1, 2, 3

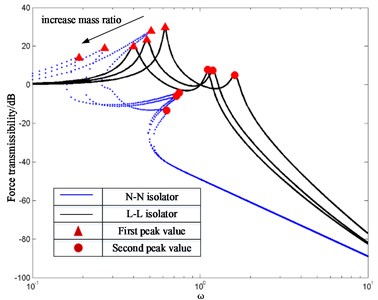
Fig. 13FT of N-N isolator and L-L isolator with different damping ratios

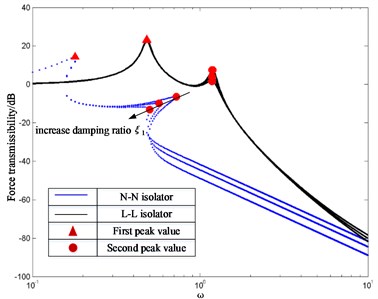
a) Effect of regular ${\xi }_2$ and variable ${\xi }_1$ where $f=$ 0.1, ${\xi }_2=$ 0.03, $\mu =$ 2 and ${\xi }_1=$ 0.01, 0.03, 0.05

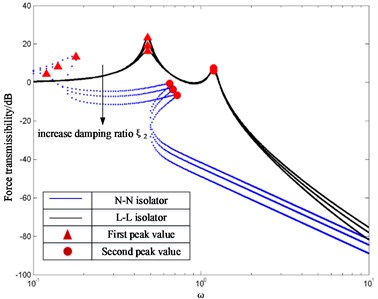
b) Effect of regular ${\xi }_1$ and variable ${\xi }_2$ where $f=$ 0.1, ${\xi }_1=$ 0.03, $\mu =$ 2 and ${\xi }_2=$ 0.01, 0.03, 0.05