Rubbing dynamics behavior of a flywheel shafting with a single point flexible support

2.1. Spin test system diagram and its dynamic model

Fig. 1 shows a diagram of the flywheel spin test system, which is composed of the flywheel rotor, stop, disk type motor, pivot-jewel bearing, oil damper and some vibration sensors. The whole spin test system is installed in a vacuum container. a stop is designed and installed inside the flywheel hollow top. There is a suitable gap between the stop and flywheel rotor. The gap is very small, and the order of magnitude is about several hundred microns. The stop is used to suppress the vibration amplitude when it exceeds the gap. When the flywheel starts up, the stop will act, especially when the flywheel is beginning to accelerate.

Fig. 1The flywheel shafting system

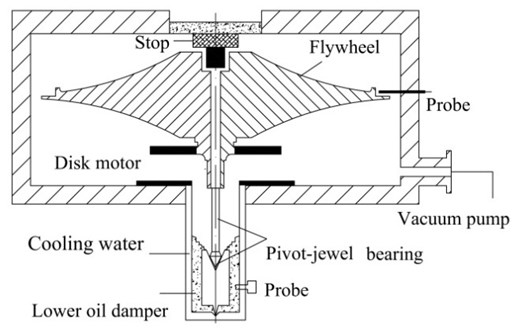
The designed stop controls vibrations inside the gap. The vibration energy will be absorbed and dissipated by collision and friction when the flywheel starts up. Because the stiffness of pivot is very small, the stiffness of the stop is designed much higher.

The disk type motor is composed of disk type rotor and disk type stator. The disk type rotor is integrated with the flywheel rotor, and the structure is very compact. The heat produced by disk stator is transferred by a cooling system which is also used by the lower oil damper.

The pivot jewel bearing is lubricated with oil baths. The pivot top is directly inside the lubricating oil. The diameter of the circular arc at the top of the pivot is only 2 mm, and contact area between pivot top and jewel bearing is less than 1.5 mm². The friction loss is very small. The pivot is made of high temperature carbon steel, and the jewel material is corundum, so the service life of pivot jewel bearing is very long, which is about tens of thousands of hours. The pivot jewel bearing can be used in the super high vacuum environments. the jewel bearing is set on the top of damping body which connects the mechanical housing with three flexible springs. The springs provide radial stiffness for the low support of the flywheel. the viscosity of the oil in the damper is relatively large, which provides viscous damping effect for the lower support of the flywheel. Obviously, viscous damping can suppress flywheel vibration, and can also lubricate bearings and dissipate friction heat.

The flywheel shafting has no upper support, so the lower damper is very important for dynamic characteristics. Based on its working principle, the damper is simplified to spring-oscillator model with a single degree of freedom. the eddy current sensor installed inside the shell of damper is used to measure the vibration response of damping body by excitation. The equivalent mass, stiffness and damping coefficient of the lower damper can be derived according to vibration theory of the single degree of freedom.

Fig. 2The dynamic model

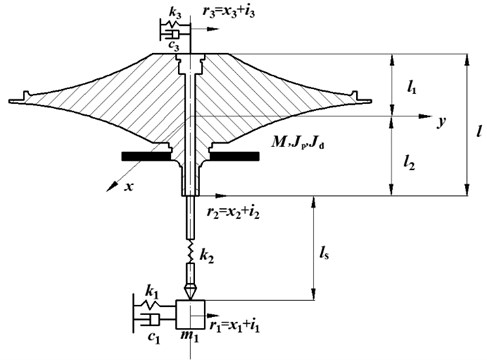
The dynamic model is as shown in Fig. 2. in order to simulate conveniently, the complex vibration displacement $r\left(r=x+iy\right)$ is used to represent the vibration displacements in the $x$ and $y$ directions. the symbols in Fig. 2 are listed in the Nomenclature.

2.2. The dynamics modeling of the flywheel shafting system

The dynamic model of flywheel shafting system is as shown in Fig. 2. The rotating kinetic function $T_i$, the potential energy function $U_i$, and the consumed energy function $Z_i$ are obtained by Lagrangian equation.

1) The spring squeeze film damper:

2) The pivot has stiffness and no mass:

3) The flywheel:

4) The dynamic model when stop acts:

The free vibration equation of the flywheel shafting system is obtained in the matrix form by Lagrange method:

The first and second order differential of vibration displacement column vector are represented $\left\{\dot{r}\right\}$ and $\left\{\ddot{r}\right\}$. $\left\{r\right\}=\left[\begin{array}{lll}{r}_1& r_2& r_3\end{array}\right]$, and $r_j=x_j+i{y}_j$, $\left(j=1,2,3\right)$. State vector method can be used to solve Eq. (5), whose solution form is:

The complex vibration amplitudes and complex frequencies are:

In which, $\lambda$ is the mode decaying exponent, $\omega =2\pi f$ is the mode angular frequency and $f$ is the modal frequency. The modal damping ratio $\zeta =-\lambda /\omega$, and if $\lambda >0$, the dynamic system is stable. the larger $\left|\zeta \right|$ is, the better stability the system has. So, the modal frequencies, mode shapes and modal damping ratios of the flywheel system were obtained by solving Eq. (5). in engineering practice, the flywheel rotor inevitably exists unbalance, if the residual unbalance is $\left\{f\right\}=\left\{u\right\}{\omega }^2{e}^{i\omega t}$ at the flywheel rotor top, the forced vibration equation of the flywheel dynamic system is got by means of the Lagrangian equation. The steady state unbalance response was calculated from Eq. (8):

3.1. Critical speeds

Fig. 3 shows the Campbell diagram. in Fig. 3, ‘1F’ and ‘1B’ indicate the first-order forward and backward whirl of the flywheel respectively. ‘LDF’ and ‘LDB’ indicate the forward and backward whirl of the lower damper respectively. ‘2F’ and ‘2B’ indicate the second-order forward and backward whirl of the flywheel respectively.

From the Fig. 3, the mode frequencies at different speeds are presented. The flywheel rotor is generally flat rotor, which has strong gyroscopic effect due to angular component. The modal frequency varies with the rotating speed. The first-order mode of the flywheel shafting divides into forward and backward modes, as well as the second-order mode. The forward frequency is increased as the speed increases, while the backward frequency is decreased as the speed increases. the shape of the flywheel rotor, the mass and the inertia moment distribution are the main sources of modal frequency variation.

Fig. 3The Campbell diagram

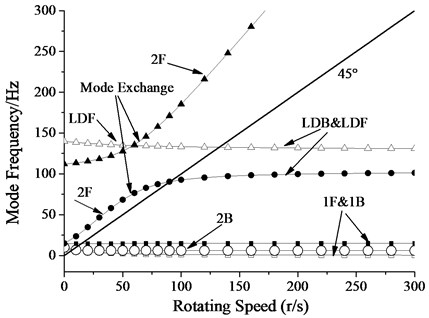
In this case, the gyroscopic effect mainly affects the second-order modes of the flywheel. The gyroscopic effect essentially enhances the stiffness of the flywheel shafting with the increasing rotating speed for the second-order forward whirl. This effect is just the opposite for the second-order backward whirl. For the first-order modes, the effect is small. The conical mode of the flywheel rotor exchanges with the lower damper mode when it rotates at 4200 rpm-5400 rpm. The exchange of modes completes when the rotating speed exceeds 6000 rpm. When the forward whirl frequency and speed frequency are the same, the corresponding speed is the critical speed, and generally corresponds to the amplitude peak. for the dynamic system as shown in Fig. 2, the critical speeds are 900 rpm (1st mode) and 7800 rpm (Lower damper mode). It is found that the flexible pivot greatly decreases the critical speeds.

3.2. Mode shapes

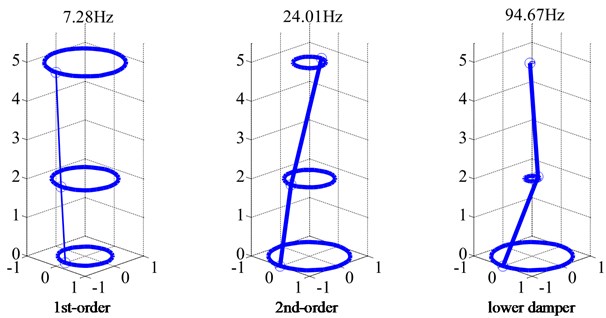
The mode shapes at the critical speeds are as shown in Fig. 4(a) and Fig. 4(b) respectively: the flywheel top, the flywheel bottom and the lower damper are displayed as three hollow dots from top to bottom in the two figures respectively.

Fig. 3 and Fig. 4 show that the conical mode of the flywheel exchanges with the lower damper mode when modal frequencies are close to each other. The vibration amplitude of the flywheel decreases in the lower damper mode, and it increases in the conical mode. the amplitude of the lower damper gradually decreases in the conical mode. It is the zone of dual mode shapes when in the speed range 900 rpm-7800 rpm. The exchange of modes completes basically when the rotating speed exceeds 6000 rpm.

When the rotating speed is 6000 rpm, the mode shapes of the flywheel shafting are shown in Fig. 5. The flywheel passes through the zones of cylindrical mode and dual modes in the spin test. Compared with conventional bearings, the stiffness of both elastic pivot and lower damper is very small, which makes their mode frequencies so close. The exchange of mode shapes occurs in a narrow frequency range is a new kind of dynamic characteristics produced by flexible damping support.

Fig. 4Mode shapes of the flywheel shafting

a) Rotating speed: 900 rpm

b) Rotating speed: 7800 rpm

Fig. 5Mode shapes (rotating speed: 6000 rpm)

a)

b)

c)

In order to test the flywheel structure strength, rotating speed is generally over 48000 rpm. Fig. 6 shows the mode shapes of the flywheel shafting. The modal frequency of the second-order mode is 1132.9 Hz, which is larger than 800 Hz, so it will not be shown in the test. The lower damper mode shape is displayed as circular motion of damping body, while flywheel is fixed. The first-order mode shape of the flywheel is still cylindrical mode.

Fig. 6Mode shapes (rotating speed: 48000 rpm)

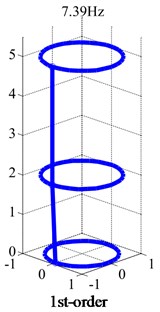
a)

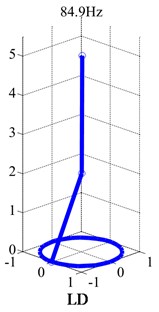
b)

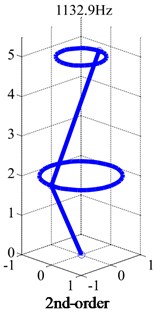
c)

3.3. Modal damping ratios

The modal damping is obtained by solving Eq. (5) to assess the stability of the flywheel shafting. The modal damping ratio varies with the rotating speed, which is shown in Fig. 7. Due to no bearing at the flywheel top, the flywheel is leaning against the inside of the flywheel top when the rotating speed is zero. Obviously, the flywheel shafting is unstable when it starts up. with the increase of rotating speed, gyroscopic effect of flywheel is becoming larger and larger, and vibration energy of the flywheel is dissipated quickly through collision and friction inside the gap between the flywheel and stop, then flywheel is rotating stably. $k_3$ is 10⁴ N/m when the stop acts, and $k_3$ is 0 N/m when flywheel is rotating stably. The modal damping ratios of each mode are obtained when the stop acts or not.

Fig. 7The modal damping ratios

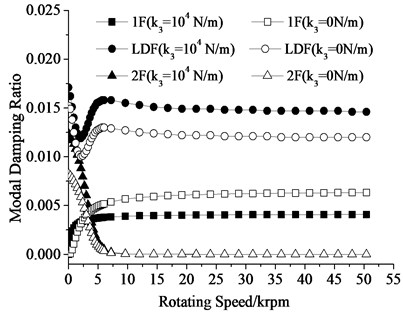
The dynamics of the flywheel shafting is stable when its modal damping ratios are positive for forward whirl modes. The larger the modal damping ratio is, the faster the complex vibration displacement $r$ attenuates. The system has better dynamic stability. So, the modal damping ratios have an obvious impact on the performance.

Fig. 7 indicates the modal ratio of the first-order mode is becoming larger with the rotating speed is increasing, which is more than 0.005. The modal ratio of the second-order mode is becoming smaller with the rotating speed is dropping. However, it is still positive. Due to the second-order modal frequency is always much higher than its rotating speed, it will not appear in the spin test. The ratio of the lower damper mode is becoming larger with the rotating speed is increasing, and slowing shrieking to 0.012. The stop mainly affects the first-order mode and the lower damper mode, and plays only a small part on the second-order mode. The flywheel shafting has good stability whether the stop works or not.

4.1. Critical speeds

For theoretical calculation, when the forward whirl frequency and speed frequency are the same, the corresponding speed is the critical speed, and generally corresponds to the amplitude peak. for the dynamic system as shown in Fig. 2 of section 3.1, the critical speeds are 900 rpm (1st mode) and 7800 rpm (Lower damper mode).

Fig. 8Critical speeds of the flywheel shafting (lower damper)

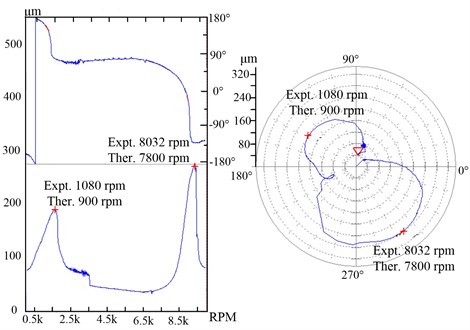
For the experiments, the eddy current sensors also installed in the lower damper can measure the forced vibration responses of the damping body. The sensors were installed at central section of the lower damper. the electrical signal by the preamplifier was input to the oscilloscope. The amplitude-frequency curve of the damping body in the lower damper can be obtained by FFT analysis.

Fig. 8 showed the amplitude-frequency response, its Bode map and Nyquist map. The critical speeds would be obtained from Fig. 8. The flywheel ran up to 10000 rpm steadily. The flywheel shafting system had two critical speeds. The first critical speed was 1080 rpm, whose theoretical result was 900 rpm. The relative error was 16.7 %. the phase angle changed from 180° to 90°. The amplitude at the first critical speed was about 140 μm. The second critical speed was 8032 rpm, whose theoretical result was 7800 rpm. the relative error was just 2.9 %. The phase angle changed from 90° to 135°. The amplitude at the second critical speed was about 256 μm. It was found that the numerical results were close to the measured data, which indicated that the dynamic model well described the dynamic behavior. When the flywheel passed the two critical speeds, the vibration amplitude shrank rapidly with the increase of the speed, which was the self-centering effect of the rotating flywheel.

4.2. The forced vibration response

The residual unbalance of the flywheel rotor was 0.1 g·cm∠37° by dynamic balance test, the steady state unbalance responses could be calculated by Eq. (8). The vibrations of the flywheel shafting were measured at the different damping and stiffness in the experiment, which verified the correctness of the dynamics modeling and simulation.

For the flywheel shafting shown in Fig. 1 and Fig. 2, the stiffness and damping of the lower damper were easier to adjust. the equivalent mass of the damper was determined by the mass of the damping body. The equivalent damping coefficient was determined by the viscosity of the damping medium. The equivalent stiffness was determined by the three small stiffness springs.

Based on its working principle, the damper was simplified to spring-oscillator model with a single degree of freedom. The eddy current sensor installed inside the shell of damper was used to measure the vibration response of damping body by excitation. The equivalent mass, stiffness and damping coefficient of the lower damper could be derived according to vibration theory of the single degree of freedom.

The vacuum oil Mobil 1 and Mobil 68 were used to revise the damping coefficient $c_1$. The springs with different thickness were chosen to change the stiffness $k_1$. Four different stiffness and damping coefficients were used to carry out the spin test. the $k_1$ was 586 N/m or 2546 N/m respectively, and $c_1$ was 0.7 N·s/m or 1.7 N·s/m. The other dynamic parameters were consistent with ones in section 3.

The eddy current sensors installed in the lower damper can measure the forced vibration responses of the damping body. When $c_1$ was 0.7 N·s/m or 1.7 N·s/m, and $k_1$ was 586 N/m, the effect of damping on amplitude – frequency response was shown in Fig. 9.

Fig. 9The effect of damping on amplitude – frequency response

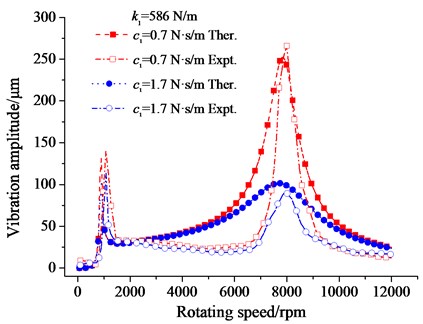
When $c_1$ was 0.7 N·s/m, the first critical speed measured was 1080 rpm, the theoretical result was 900 rpm, the second critical speed measured was 8032 rpm, the theoretical result was 7800 rpm. When $c_1$ was 1.7 N·s/m, the critical speeds were almost no change, which showed the damping coefficient had little effect on the critical speeds of the shafting.

However, increasing damping coefficient could significantly suppress the amplitude of the vibration when the flywheel passed the two critical speeds. Fig. 9 showed the theoretical calculations of the amplitude were in good agreement with values measured in the experiment, especially when speed was near the critical speeds. The experimental values were slightly smaller than the calculated values in the zone away from the critical speeds.

Fig. 10The effect of stiffness on amplitude – frequency response

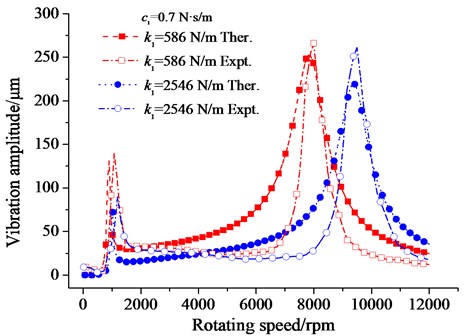
Fig. 10 showed the effect of stiffness on amplitude – frequency response. The larger stiffness increased the critical speeds greatly, which made difficulty to pass the critical speeds. The first critical speed increased from 1080 rpm to 1200 rpm, and the second critical speed increased from 8032 rpm to 9652 rpm. The larger stiffness had little effect on the vibration amplitude when passed the second critical speed. However, the larger stiffness could reduce the amplitude when passed the first critical speed, which from 135 μm to 75 μm.

Fig. 11The combination of stiffness and damping

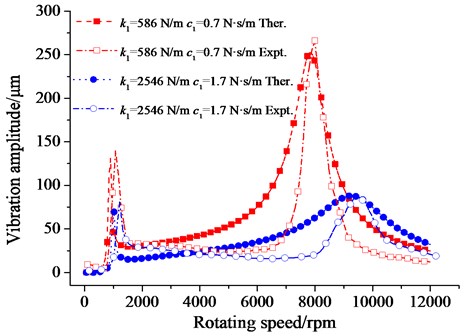
Through the above discussion, the larger damping mainly suppressed vibration amplitude, and had little effect on critical speeds. The larger stiffness mainly increased the critical speeds, and had little effect on vibration amplitude, which was confirmed again in Fig. 11.

One perfect set of rotor dynamics parameters was selected for the spin test system. The $k_1$ 586 N/m and $c_1$ 1.7 N·s/m were the most appropriate in the four sets of dynamic parameters. Based on the tests above, the comparison between the calculated unbalance response and the experimental response indicated that the dynamic model was proper.

5.1. Rubbing to start-up

As shown in Fig. 12, the orbits showed the flywheel rotor contacted the stop occasionally at the beginning of rubbing to start-up. The vibration amplitude remained at almost the value of the gap when the stop acted, which was about 0.2 mm. The stop restricted the amplitude of the vibration very effectively with the rotating speed was increasing. the impact and the friction between the flywheel and the stop suppressed the vibration of the flywheel. When the motor speed reached about 960 rpm, the flywheel was rotating stably. The constant output of the rotation speed transducer indicated that the friction torque had not exceeded the motor-driven torque.

Fig. 12Rubbing to start-up (gap = 0.2 mm)

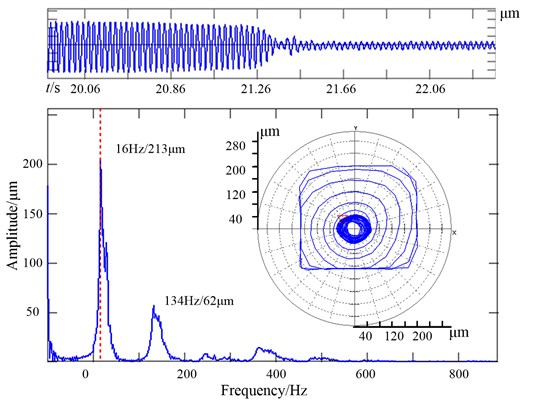
The vibration waveform and orbits in Fig. 12 showed vibration energy of the flywheel was dissipated quickly through rubbing inside the gap between flywheel and stop. The stop would not act after rubbing to start up, which because the vibration amplitude was much smaller than the gap between the stop and flywheel. Fig. 12 showed the vibration amplitude was about 60 μm after rubbing to start up, while the gap was 0.2 mm.

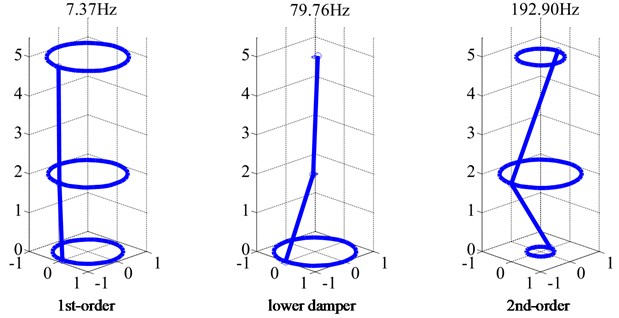
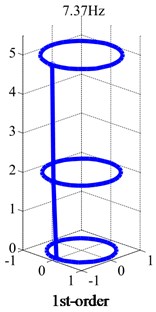
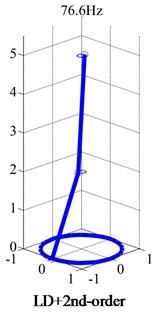
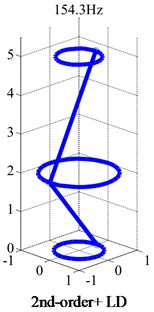
The FFT analysis in Fig. 12 showed the shafting had two frequencies which were 16 Hz and 134 Hz. as shown in Fig. 3, the 1st-order and 2nd-order critical speeds are 900 rpm and 7800 rpm respectively. Obviously, the two frequencies were in good agreement with critical speeds by the simulation. The rotor rotated counterclockwise. Obviously, the vibration consisted of two kinds of rotation frequencies.

There are many dynamic parameters which may affect rubbing to start-up, such as stiffness of the stop, rubbing friction coefficient, gap, and so on. However, the gap’s effect on rubbing to start-up will be discussed in this paper. The influences of other dynamic parameters on rubbing to start-up will be gradually studied in the follow-up.

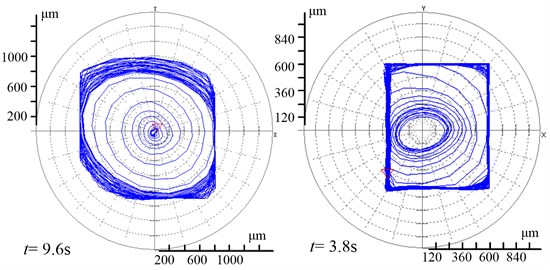
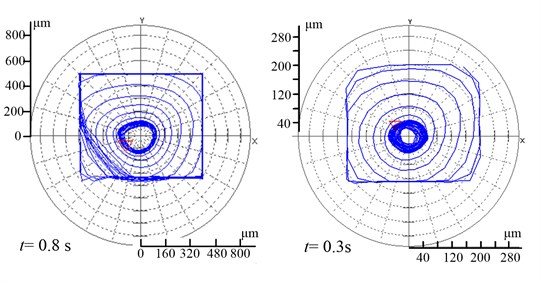
Fig. 13 showed orbits of rubbing to start-up with four different gaps. It can be seen that the bigger gap had the longer time for rubbing to start-up. It took 9.6 s to rotate stably when the gap was 0.8 mm, while just 0.3 s when the gap was 0.2 mm. The shorter time will also reduce the damage to the stop and flywheel rotor. It is necessary to choose a smaller gap in the test.

Fig. 13a) gap = 0.8 mm and 0.6 mm, b) gap = 0.4 mm and 0.2 mm

a)

b)

5.2. Excitation to destruction

For the flywheel spin test, especially the composite flywheel endured high-speed centrifugal force, resin minor damages and fiber part breaks will produce non-ignorable disturbances, which causes shafting that has small modal damping ratios to natural whirl modes with low frequencies. Because the flywheel is rotating at a high speed in a spin test, the low frequency vibration will threaten flywheel life and structural strength seriously, such as causing rubbing to damage between stop and flywheel. It is necessary to study how and when the low-frequencies affect dynamic characteristics of the shafting.

The certain external harmonic excitation force was used to simulate the low frequency produced by sudden unbalances. The following steps were performed in the rubbing experiments. Firstly, the flywheel was brought to rubbing to start up and rotated steadily at the speed of 3000 rpm. The rubbing inside the gap was induced by low frequency excitation force, which was at the top of the flywheel in the $x_1$ direction. The magnitude and direction of the excitation force were adjustable and had the properties of harmonics. The use of low frequency excitation force was mainly based on the following reasons. It can be seen from Fig. 7 that the mode damping ratio of conical mode was very small, which had poor dynamic stability. Using low frequency excitation to induce conical mode was easy to achieve.

The exciter is an electromagnetic actor. It was set close to the flywheel top to perturb the magnetic field. The sinusoid signal from the signal generator was amplified and then drove the exciter to generate a synchronous harmonic excitation. the frequency of the excitation and the amplitude vary to satisfy the experiments. to measure the excitation amplitude, a DC volt was applied to the electromagnetic actor, which led to the flywheel drifting off the central axis of the bearings. Then a compensation elastic force pushes the flywheel to its original center position. on measuring the elastic force, one obtains the relation between the DC volt and the force.

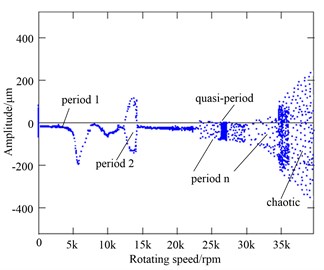
Firstly, the flywheel was brought to rubbing to start up and rotated steadily at the speed of 3000 rpm. The transducers and data test systems measured and recorded the dynamic behavior of the rotating flywheel, including the vibration time history, the frequency spectrum of vibration and the orbits of the flywheel center. Fig. 14(a) and (b) showed the shafting was in a motion of period 1. The axis orbit was a regular ellipse. The FFT analysis showed there was only one speed frequency.

Fig. 14The route of excitation to destruction

a) Bifurcation diagram

b) Period 1

c) Period 2

d) Period 3

e) Period 2

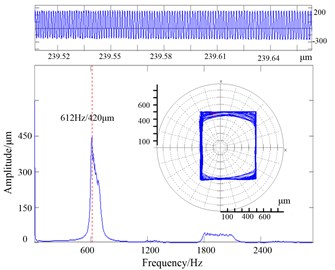
f) Period 3

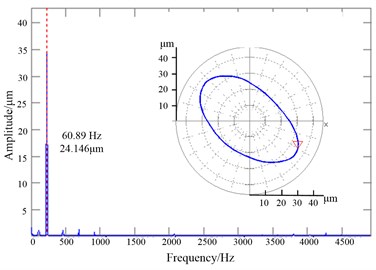
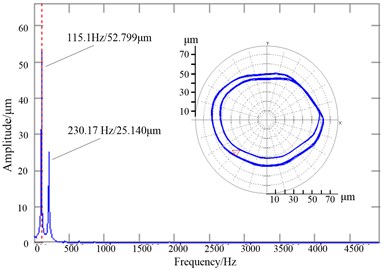
Then the proper excitation frequency of 115.1 Hz was found to obtain a large response of the flywheel top when the flywheel was rotating at a speed of 230.17 r/s. at that frequency, the excitation force was increased until the peak amplitude of flywheel whirl became larger and larger. The flywheel/stop gap was adjusted to 0.3 mm, which was much larger than the vibration amplitude of the flywheel in normal operation. It can be seen from Fig. 14(a) and (c) the shafting went into period-doubling bifurcation motion. The periodic motion was composed of two low frequency motions, which were 115.1 Hz and 230.17 Hz individually. Obviously, the motion behavior was similar to the half frequency whirl, and the frequency of 115.1 Hz was being very near to the second order critical frequency 130 Hz. It can be seen from Fig. 14(a) the shafting reentered in a motion of period 1 when the excitation frequency and excitation force were canceled.

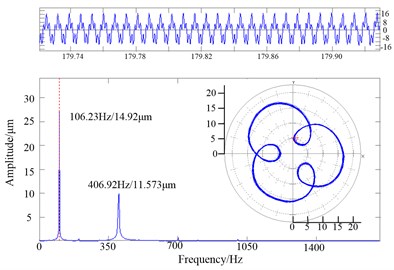
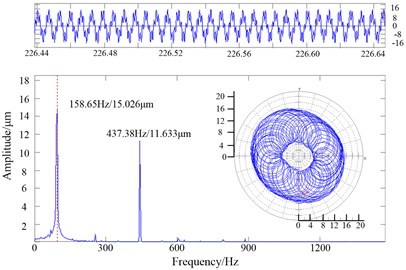
Fig. 14(d) was the vibration waveform of the flywheel excited by the excitation frequency of 106.23 Hz, and the orbit of the flywheel center was also shown in Fig. 14(d). The vibration amplitude was not large enough to exceed the gap between the flywheel and the stop. Spectrum analysis indicated that the vibration without rubbing was the double-frequency whirl composed of the excitation frequency 106.23 Hz whirl with large amplitude 14.92 μm and the synchronic 406.9 Hz whirl with small amplitude 11.57 μm. at that frequency, the shafting went into period 3 bifurcation motion. at the same way the shafting went into quasi-period motion when the proper excitation frequency was 158.65 Hz as shown in Fig. 14(e). It can be inferred that the excitation frequency was basically around the 2nd-order critical speed. It was indirectly proved that the mechanical model was proper.

The flywheel/stop gap was adjusted to 0.3 mm, which was much larger than the vibration amplitude of the flywheel in normal operation. The vibration amplitude was becoming larger as the excitation force increased. the excitation frequency was keeping around 130 Hz, which was near to the second order critical speed. When the speed reached to 36000 rpm, the motion was evolved from quasi-periodic motion to chaotic motion. The amplitude was getting bigger and bigger, and the axis orbit was becoming more and more chaotic till the full rubbing happened. The full rubbing was accompanied by a continuous collision and friction inside the gap. The center of the flywheel moved counter-clockwise and whipped in the amplitude exceeding the rotor/stop gap dramatically.

The vibrating flywheel went into whipping at a much higher frequency with amplitudes larger than the flywheel/stop gap. The flywheel rolled on the stop without separation. The continuous full rubbing slowed down the rotating speed of the flywheel. in order to observe the full rubbing behavior, the drive power of the motor was keeping large enough. The rubbing speed was increasing slowly. It can be seen from Fig. 14(a) and (f) the orbit of the flywheel center was like a square. The vibration signal consisted of two kinds of periodic motion by spectrum analysis. The rotating speed frequency was 612 Hz, and the high frequency band excited by rubbing was 1800-2200 Hz. The rotating speed frequency was 612 Hz, and corresponding vibration amplitude was 420 μm which was larger than the flywheel/stop gap. the excitation low frequency was not found when the rubbing occurred. It was inferred the exciter probe had been damaged. However, the broadband signal was observed, which located between 1800 Hz and 2200 Hz, and corresponding vibration amplitudes were about dozens of microns. The bifurcation diagram showed that the flywheel was in chaotic motion from Fig. 14(a).

When the drive power was cut off, the test rotating speed of the flywheel dropped from 36720 rpm down to nearly 0 rpm in 8.6 s because of the continuous flywheel/stop friction. After the rubbing experiments, a lot of metal powder was found on the inner face of the flywheel top, which meant that the continuous serious friction destroyed the contact surface of the flywheel and the stop. It was supposed that the full rubbing occurred at high speed would directly damage the stop and flywheel top. It was difficult to suppress sub-harmonic whirl of the flywheel when the rubbing occurred at high speed. The rubbing to start up suggested that the stop worked effectively only at a low speed for rubbing to start up.