Research on local rub fault transfer mechanism in rotor system

1. Introduction

Rotating machines such as compressor are likely to develop one or more faults. The faults often occur in local, for example, rub often occurs between impeller and shell, and fatigue crack appears in a shaft section. The faults affect the whole rotor system although they only occur locally. The whole system has nonlinear response.

The eccentricity of the center of mass along the rotor axis is unavoidable. Excessive unbalance vibration is one of the reasons for the local rub fault. The fault can increase the vibration of the rotor system and create an unstable dynamic behavior.

In order to avoid instability, the influence of the local faults on the whole rotor system must be performed carefully. Therefore, the nonlinear dynamic behavior in the local fault rotor system is researched in this study. The research on the nonlinear response can be divided into four stages: numerical and L-P perturbation method, traditional analytic method (such as KBM, averaging and multi scales method), generalized perturbation method (such as circular and elliptic function, generalized harmonic function method), and comprehensive method (such as incremental harmonic balance method). From weak nonlinear system to strong nonlinear system, applicability of the methods is more and more comprehensive. L-P perturbation method and traditional analytic method are suitable for weak nonlinear system, and generalized perturbation method, incremental harmonic balance method and numerical method are not only suitable for weakly nonlinear but also for strong nonlinear system. The methods are widely used at present [1-5].

The above research methods can be divided into theoretical analysis and measurement method. The theoretical analysis method includes the analytical method, the numerical method, and the semi-analytical semi-numerical method: incremental harmonic balance method (IHB) [6, 7]. Qian Zhao et al. [8] proposed the method that combines the IHB method with the finite element method to predict the dynamic stress and deformation of rubbing blades. Yao Hongliang et al. [9] proposed the dimension-reductive incremental harmonic balance method to increase the computational efficiency. IHB method is suitable for both weak nonlinear and strong nonlinear system. It is not limited by small parameters.

Based on the L-P method, the improved L-P method, the elliptic function L-P method, the generalized L-P method, and so on, are used to solve nonlinear equation in the analytical method. Paolo Amore and Alfredo Aranda [10] applied the Linear Delta Expansion to the L-P method to find improved approximate solutions to nonlinear problems. R. R. Pusenjak [11] presented the extended L-P method with multiple time variables to solve the unsteady vibration of the cubic nonlinear term in the dynamical system. L-P, KBM and averaging is suitable for weak nonlinear system. Generalized perturbation method is suitable for strong nonlinear system.

Analytical solution is obtained by the analytical method. It is easy to facilitate the analysis of dynamic characteristics and parameter control. But most nonlinear equation of multiple degrees of freedom cannot obtain analytical expression. The numerical method overcomes this problem and becomes an important method to solve nonlinear equation, e.g. Runge-Kutta method [12], Newmark method [13], etc. Tejas H. Patel and Ashish K. Darpe[14] used the four order Runge-Kutta method to examine vibration response of the cracked rotor in presence of common rotor faults. Junyi Cao et al. [15] used four order Runge-Kutta method and ten order CFE-Euler method to simulate and calculate the dynamic equation of the rubbing rotor system with fractional order rubbing, and obtained a large number of non-linear characteristics. A Sung Lee et al. [16] proposed the state-space Newmark method to analyze the transient vibration response of the rotor-bearing system. Mzaki Dakel et al. [17] presented the implicit Newmark time-step integration scheme to analyze the transient response of the rotor-bearing system. Yao Hongliang et al. [18] analyzed the dynamic characteristics of rub rotor and proposed model-based rub fault diagnosis method using Newton-Raphson method. Compared to Runge-Kutta method, Newmark method is more suitable for equation of more degrees of freedom. However, the calculation speed of the numerical method is decreased due to more degree of freedom.

Value of the generalized coordinate is obtained by the numerical solution at any time of the system. The value often can be used as a standard to test the results of the analytical method. However, the numerical solution has the problem of convergence and accuracy, and can only provide discrete solutions, cannot give a specific expression.

The measurement method is to measure directly nonlinear response of the fault rotor system. It is usually used to verify the theoretical method or directly analyze nonlinear characteristics of the system. Fulei Chu and Wenxiu Lu [19] installed an experimental setup to simulate the rotor-to-stator rub of the rotor system. Tejas H. Patel and Ashish K. Darpe [20] used the measurement method to study the dynamics of misaligned rotors and reducing the ambiguity so as to improve the reliability of the misalignment fault diagnosis.

The measurement method can directly and quickly measure nonlinear response of the fault rotor system without solving differential equation. But in engineering practice, rotating machinery cannot place sensor to measure response at some positions. So, the measurement method cannot meet the needs.

In order to solve the problem of nonlinear response in the fault rotor system, the local rub fault transfer mechanism of the rotor system is presented. Influence of the local rub on the other positions is obtained. The finite element model of the local rub rotor system is established and the steady-state nonlinear response is obtained by numerical method. Based on the harmonic balance theory, the fault transfer mechanism is deduced by the relationship between the harmonic components of vibration response and the frequency response matrices in the fault rotor system. The response of any other node is obtained by the fault transfer mechanism. The correctness of the transfer mechanism is verified by numerical simulation and experiment.

2. Finite element model of rotor system

Applying the Lagrange’s equation, equation of motion of the fault rotor system of n nodes may be expressed by the following:

where $\mathbf{x}={\left[x_1,{\theta }_{y1},x_2,{\theta }_{y2},\cdots x_n,{\theta }_{yn},y_1,-{\theta }_{x1},y_2,-{\theta }_{x2},\cdots ,y_n,-{\theta }_{xn}\right]}^T\text{.}$$x$, $y$, ${\theta }_x$ and ${\theta }_y$ represent translational and rotational displacements in the x and y directions in radial direction respectively. Any displacement in axial direction is neglected. $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ represent mass, damping and stiffness matrix of the rotor system respectively. ${\mathbf{F}}_{unb}$ and ${\mathbf{F}}_{rub}$ represent unbalance and rub forces respectively. The system matrices and external force vectors are given in the Appendix A.

3. Local rub fault transfer mechanism

The unbalance force and rub fault force are periodic in the rotating machinery. They can be expanded into the form of harmonic components by the following:

where:

are position vectors of the external force. $L_{unb}$ and $L_{rub}$ are the node positions of the force. $j=\sqrt{-1}$. $\omega$ is the rotating speed. $A_1$ and $B_2$ are harmonic coefficient of the external force.

The response of the system is also expanded into the form of harmonic components by the following:

Substituting Eqs. (2) and (3) into Eq. (1), according to the harmonic balance theory, the harmonic coefficients are:

where $l$ is the order of the harmonic component. The Eq. (4) is rewritten as:

where:

Assuming that ${\mathbf{x}}_{l\left(2L_{rub}-1\right)}{e}^{j\omega tl}$, ${\mathbf{x}}_{l\left(2k-1\right)}{e}^{j\omega tl}$, ${\mathbf{x}}_{l\left(2k_1-1\right)}{e}^{j\omega tl}$ and ${\mathbf{x}}_{l\left(2k_2-1\right)}{e}^{j\omega tl}$ are the $l$th order harmonic component of response on rub node, node $k$, $k_1$ and $k_2$, respectively. The ratio of ${\mathbf{x}}_{l\left(2k_1-1\right)}{e}^{j\omega tl}$ to ${\mathbf{x}}_{l\left(2k_2-1\right)}{e}^{j\omega tl}$ is:

Substituting Eq. (5) into Eq. (7), the Eq. (7) is rewritten as:

$A_l$ and $B_l$ can be expressed from Eq. (8):

The $l$th order harmonic component of response on node $k$ is obtained by the following:

The response on node $k$ can be expressed:

The response of any other node may be obtained by the fault transfer mechanism when local rub fault occurs in the rotor system, that is, influence of the local rub on the other positions can be obtained. The local rub force may be obtained by Eq. (2).

4. Results

4.1. Numerical simulations

The finite element model of the local rub fault rotor system is established as shown in Fig. 1. The model is composed of 2 rigid disks, 42 finite shaft elements and 2 bearings. Values of the system parameter used for the numerical simulations are as follow: elasticity modulus, $E=$ 210 GPa; shaft length, $L_s=$ 15 mm; shaft diameter, $D_s=$ 10 mm; disk length, $L_d=$ 25 mm; disk diameter, $D_d=$ 75 mm; supporting stiffness, $k=$ 1×10⁶ Nm^-1; supporting damping, $c=$ 7×10⁴ Nsm^-1; eccentric mass, $m_e=$ 5×10^-6 kg; unbalance eccentricity, $e=$ 2 mm; coefficient of friction, ${\mu }_{rub}=$ 0.15; rub stiffness, $k_{rub}=$ 2×10⁵ Nm^-1. The Unbalance force is at node 30. The rub fault is at node 10. The measuring points are at nodes 6, 21 and 24, respectively. Analysis is carried out in MATLAB programming.

Fig. 1Finite element model of rub rotor system

The Newmark method in conjunction with Newton-Raphson scheme (Newmark-Newton) is used to solve the nonlinear response of the system when $\omega =$ 500 rad/s. The Newmark-Newton method is given in the Appendix A. The response curves of the measuring nodes and the rub node in the x direction are shown in Fig. 2. It can be seen that the time domain response is periodic, and the center of the vibration deviates from the equilibrium position due to the presence of the local rub fault. The response of the whole system is affected by the local rub fault.

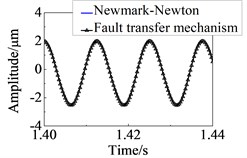
The responses of the nodes 6, 21 and the rub node are used to solve the response of the other nodes in the rotor system by the fault transfer mechanism. The response curves of the node 24 using Newmark method and the fault transfer mechanism are shown in Fig. 3. It can be seen that the two curves are perfectly coincident. It is proved that the fault transfer mechanism can be used to solve the nonlinear response of the local rub fault rotor system.

The curves of the rub force can be obtained shown in Fig. 4. It can be seen that the two curves are substantially coincident.

Fig. 2Response curve in time domain

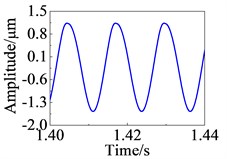
a) Node 6

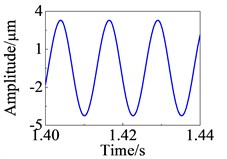
b) Node 21

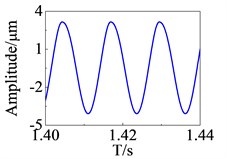
c) Rub node

Fig. 3Response curve in time domain at node 24

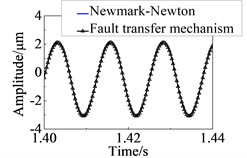
a)$x$ direction

b)$y$ direction

Fig. 4Calculation results to rub force

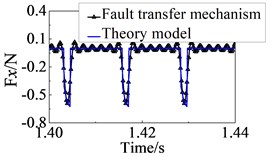
a)$x$ direction

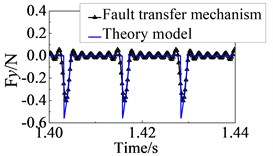
b)$y$ direction

4.2. Experimental results

Experiments are carried out by using the Bently rotor test rig and B&K3560B signal collector. Experimental equipment is shown in Fig. 5. The dynamic model of the Bently rotor test rig is the same as the numerical simulation model. The points of rub and eccentricity are at nodes 16 and 34, respectively. The sensors are placed at nodes 9, 15, 21, and 31, respectively. Measurement data are collected at rotor operating speed of 3600 n/min. The sampling frequency is 3.2 kHz.

Fig. 5Experimental equipment

Fig. 6 shows the response curves of node 21 when the rub fault occurs. The operating state and stability of the system are judged according to the time history curve [21]. The rotor system is in a stable state. The center of the vibration deviates from the equilibrium position due to the presence of the local rub fault. 1X frequency is still dominant, 2X-6X appear in the frequency domain response.

Fig. 6Response curves at node 21

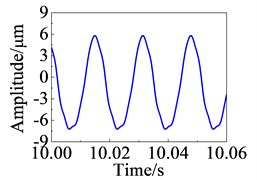
a) Time domain

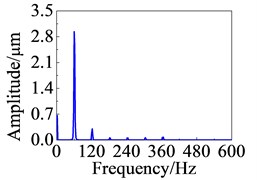
b) Frequency domain

The first six-order harmonic components are used to solve the response of node 21 by the fault transfer mechanism. Fig. 7 is the analytical results. It can be seen that the harmonic components of each order are almost coincident except 1X and 6X. The response curves obtained by measured and calculated by the proposed method also substantially coincident. The proposed method and the numerical simulations are verified from experimental investigations.

Fig. 7Comparison of experimental and theoretical results

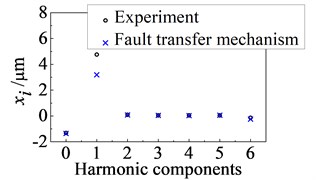
a) Harmonic components

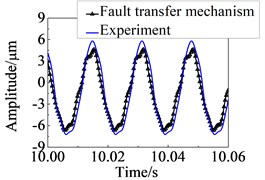
b) Response curves in time domain

5. Discussions

(1) The idea of the manuscript comes from an engineering problem. The local rub fault occurred in a compressor rotor system. The fault had been very serious when it was detected. The sensors of the monitoring system were placed on the bearing (This is a common method to place the sensors). The location of the fault was between impeller and shell, this location was far from the sensors, so the early rub fault was not detected by the monitoring system because of the distance between the location of the fault and sensors. The impeller could only be replaced when the fault was detected.

In order to improve efficiency, the clearance between stator and rotor is getting smaller and smaller. Some faults, such as rub and steam whirl, can be caused by excessive unbalance vibration. Some important locations, such as impeller and bearing, should be monitored to avoid further development of the fault.

The problem of the nonlinear response is a key scientific problem extracted from the engineering problem. To the author's knowledge, the local fault transfer mechanism is a novel method to obtain response of any other nodes. The unbalance response of the key locations is monitored when the system is operating normally, while the development of the fault can be monitored when the fault is occurred. The proposed method can solve the problem without changing the system structure.

(2) The local fault transfer mechanism is very suitable for calculating the response of some locations which is difficult to place sensor in engineering practice. It can be seen that the expression of the fault force is not required from the derivation process. So, the proposed method is applicable to other periodic fault besides rub in the rotor system.

Compared with the theoretical analysis, the expression of the fault force is not required and the response of some nodes is required, that is, it is possible to obtain the response when the expression of fault force acting on the system is unknown. Compared with the measurement method, sensor cannot be placed at some locations; the response of the locations cannot be measured and can be calculated by the proposed method.

It can be seen that the response of rotor system must be in steady state and periodic from the derivation process; the proposed method is not suitable for transient and aperiodic response. In addition, fault location is determined.

(3) The proposed method is discussed as following when the fault does not occur in the rotor system.

The equation of the rotor system of $n$ nodes without fault may be expressed:

The unbalance force and the response of the system are expanded into the form of harmonic components:

Substituting Eq. (13) into Eq. (12), the harmonic coefficients are:

The Eq. (14) is rewritten as:

Assuming that ${\mathbf{x}}_{l\left(2k-1\right)}{e}^{j\omega tl}$ and ${\mathbf{x}}_{l\left(2k_1-1\right)}{e}^{j\omega tl}$ are the $l$th order harmonic component of response on node $k$ and $k_1$, respectively. The ratio of ${\mathbf{x}}_{l\left(2k-1\right)}{e}^{j\omega tl}$ to ${\mathbf{x}}_{l\left(2k_2-1\right)}{e}^{j\omega tl}$ is:

Substituting Eq. (15) into Eq. (16), the Eq. (16) is rewritten as:

The $l$th order harmonic component of response on node $k$ is obtained by the following:

The response on node $k$ can be expressed:

The response of any node $k$ may be obtained by Eq. (19), that is, influence of the vibration caused by unbalance on the other positions can be obtained when fault does not occur in the rotor system. Comparing with the proposed method in section 2, the method presented in this section may be called vibration transfer mechanism.

6. Conclusions

The local fault transfer mechanism in the rotor system is presented in this paper. The finite element model of the fault rotor system is established. An exciting force caused by unbalance and a local rub force are assembled to model the rotor local fault. The fault transfer mechanism is derived by the harmonic balance theory. The Newmark method is used to solve the fault rotor equations. The experimentations are carried out to measure the response of the local rub fault rotor system in the rotor test rig. The response of three nodes is used to solve the response of the other nodes by the fault transfer mechanism. The numerical simulations results show that the two curves solved by the Newmark method and the fault transfer mechanism are perfectly coincident. The proposed method and the numerical simulations are verified from experimental investigations. The vibration transfer mechanism in rotor system is discussed.