Abstract
The plate theory of th order is constructed on the background of the Lagrangian variational formalism of analytical dynamics of continuum systems and the dimensional reduction approach of I. N. Vekua – A. A. Amosov. The plate model is defined within the configuration space, the set of field variables, and the Lagrangian density. The field variables are determined by the coefficients of the biorthogonal expansion of the spatial displacement vector field with respect to the dimensionless normal coordinate. The dynamic equations are derived as Lagrange equations of the second kind of the two-dimensional continuum system. The dynamics of the plane elastic layer is considered as an example, the normal wave propagation is described on the basis of refined plate theories of various orders, and the convergence of approximate solutions to the exact solution of the three-dimensional elastodynamics problem is analyzed for different wavenumbers.
1. Introduction
A plate is used nowadays as a mathematical model of many modern devices in machine industry. It is to be noted that in the high-frequency dynamics of composite plates the classical Kirchhoff’s and even the refined first-order shear deformation plate theories fail whereas they are quietly consistent with the low-frequency dynamics of thin-walled structures [1-6]. Moreover, the waveguide modeling requires refined plate theories; the authors of the paper [7] note that “more reliable 2D models are needed for high-frequency vibrations, wave propagation etc.”. In general, the refinement of plate models consists in the accounting of supplementary degrees of freedom in addition to the translation and rotation of the middle surface point in the plate kinematics [1, 8-11]. Such plate theories so-called “quasi-3D models” are used as well for highly anisotropic composite plates and functionally graded thin-walled structures [6, 12-14], as for the investigation of boundary layers in dynamics [15], boundary and edge waves [16-18], etc. The refined plate and shell theories can be also useful in problems of interaction of acoustic waves and thin-walled structures based on approximate diffraction models (e. g. see [19-21], and others).
Many methods of construction of refined plate and shell models can be used. The asymptotic integration approach [15] seems to be powerful and efficient method of the qualitative analysis of the plate and shell dynamics (for instance, see [22]). On the other hand, the asymptotic method does not allow one to construct the full hierarchy of solutions [23] approximating the three-dimensional solution in various norms [24]. At the same time the formal series expansion of the displacement vector, stress tensor etc. offers some features of numerical algorithm construction if such a plate model is used together with finite element [24] or meshless numerical simulation [25]. As well power series can be used [1, 4, 26, 27] as special function expansions [12, 13, 28]. One of the most powerful and universal approaches is based on generalized Fourier series [6, 9, 10, 24, 26, 29-31].
Here the higher-order plate theory based on the Lagrangian formalism of analytical mechanics of continua combined with the dimensional reduction approach [9] is used. The plate model interpreted as a two-dimensional continuum consists in the configuration space, the set of field variables being the biorthogonal expansion coefficients of the three-dimensional displacement vector field with respect to the thickness coordinate, and the Lagrangian density defined on the two-dimensional area corresponding to the plate middle surface (for more details, see [11, 31, 32]). This kind of theory so-called “elementary” allows one to satisfy the boundary conditions on the faces of a plate approximately as a result of the convergence of the sequence of two-dimensional solutions. To satisfy the boundary conditions exactly, for instance in the case of contact interaction, the mixed formulation [29, 30] can be used, or the “extended” theory [9] or can be constructed. In particular, the boundary conditions shifted from the faces onto the middle surface become constraint equations, and the constrained variational problem is solved by the Lagrange multipliers method [33]; this approach allows one to obtain consistent low-order approximations [27] but seems to be a bit too complex when the order of the theory rises.
The well investigated problem of normal wave propagation in the plane elastic layer [34] can be used to analyse the properties of the constructed theories hierarchy and the convergence of the two-dimensional solutions [35-40]. Here the normal waveforms corresponding to some specific wavenumbers are analysed; some results unpublished in the cited articles are presented.
2. Equations of the analytical dynamics of a plate as a two-dimensional Lagrangian continuum system
Let the plate be a three-dimensional elastic body: , , , with the faces and a lateral surface [11, 31-33]:
where is the smooth base surface and 2 is the plate thickness [11, 31].
The mathematical model of a plate consists in the two-dimensional manifold , with the curvilinear chart , [11]:
The covariant base vectors defined as , allow one to determine the metrics ; is the normal unit vector, and .
The linear dynamics problem statement for a plate can be based on the Hamilton principle [11, 32]:
The volumetric and surface Lagrangian densities can be written as follows [36]:
where is the spatial distribution of the displacement vector field.
The Lagrangian formalism of analytical dynamics allows one to introduce the configuration manifold with the generalized coordinates , [11, 31], so that , and the tangent fibration can be defined with the base vectors . For linear systems such as the Eq. (1) the configuration manifold becomes a Euclidian space; thus, the reduction of the three-dimensional elastodynamics problem given by Eq. (1) consists in the projection of onto its subspace [11, 36, 38]. To construct a plate theory, the biorthogonal system , is used, therefore can be interpreted as field variables of the first kind [11]: . Here is the scalar product [11, 32], and the vector components are supposed to be square integrable over [–1,1]. The density of Lagrangian can be now defined on as follows [32, 38]:
Here denotes the covariant derivative on , and the following linear operators are defined (see [11]):
The generalized stiffness for arbitrary anisotropic plates are defined as follows [11, 32, 38]:
Here are contravariant components of the elastic constants tensor .
Thus, the two-dimensional continuum system is defined on within the finite-dimensional configuration space , field variable , and the Lagrangian densities , . The dynamic equations of the generalized plate theory of th order can be obtained as Lagrange equations of the second kind [31] for the two-dimensional continuum system given by the Eq. (2) (see also [32, 38]):
Their natural boundary conditions can be represented in the following notation [32, 38]:
Finally, the initial conditions are represented as follows:
The initial-boundary value problem statement, Eq. (3-7), corresponds to the so-called “elementary” theory of plates of the th order; in other words, the boundary conditions on the faces are considered implicitly and can be satisfied only after solution’s convergence at the point 1. This theory allows one to obtain the simplest equations system and is preferable for higher orders. To satisfy the boundary conditions exactly we can formulate the “extended” theory of plates (for more details see [33]).
3. Modeling of the normal waves in the plane elastic layer on the background of the th order plate theory
Let us consider the plane problem for an elastic layer of thickness 2; here and below denotes shear modulus, denotes the Poisson ratio, and is the mass density. Let the normal waves be propagating along the axis . Finally, let us introduce the following dimensionless variables (see also [11, 35-38]):
where denotes the shear wave velocity.
Thus, accounting for the material isotropy and homogeneity, for the homogeneous boundary conditions and absence of bulk forces ( 0), and for the definition of the dilatation wave velocity , we transform the general dynamic Eqs. (3), (4) to the following dimensionless formulation derived in [36, 37]:
The displacement field in the normal wave propagating along is defined as follows [34]:
denotes the dimensionless phase velocity depending on the dimensionless wavenumber , is the amplitude vector. Substituting Eq. (10) into Eq. (9) we obtain the spectral problem defined by the Eq. (11) analogous to the one described in [35]:
The eigenvalues of the matrix , Eq. (12), depending on form the spectra of longitudinal and bending waves. The corresponding dispersion curves for the phase velocities are shown on Figs. 1 and 2 (see also [11] and [35] for the dispersion curves corresponding to the dimensionless phase frequencies). It can be seen that the curves corresponding to the phase velocities of the lowest-order longitudinal and bending modes tend to the Rayleigh wave velocity as the wavenumber rises, . All dispersion curves except the 1st one have the characteristic cross points with the line corresponding to the dilatation velocity, , 0; the exact solution of the three-dimensional elastodynamics problem [34] gives the characteristic wavenumber . The phase velocities computed on the basis of the spectral problem given by the Eqs. (11), (12) for the plate theories of the order 1, 2, 3, …, 10 are shown below in the Table 1. The same results for the phase frequencies are presented in [36]. Analyzing it, we can conclude that the solution at the point converges slowly that the at the point 0 corresponding to the locking frequencies of normal waves (see [11, 35]).
Exact solution (solid lines), theory of 20th order (dashed line), for plane strain.
Fig. 1Phase velocities c~Ph of symmetric waves, k,m={2n, N+2n+2}, n∈0,12N+1∪Z
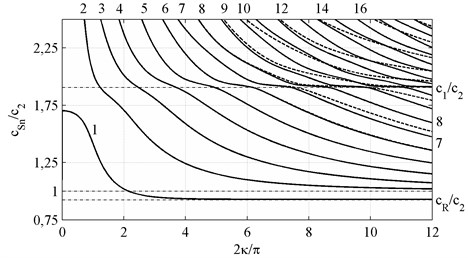
Fig. 2Phase velocities c~Ph of antisymmetric waves, k,m={2n+1, N+2n}, n∈0,12N+1∪Z
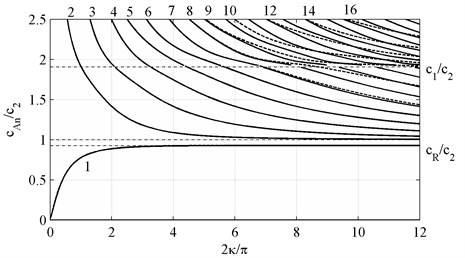
Table 1Approximate dimensionless phase velocities of longitudinal modes cPhn/c1 computed at the point κ*=πn(β-2-1)1/2 on the basis of the plate theories of the order N= 1, 2, 3, …, 10
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 1.20 | 1.13 | 1.03 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
2 | – | 1.17 | 1.14 | 1.07 | 1.04 | 1.02 | 1.01 | 1.00 | 1.00 | 1.00 |
3 | – | – | 1.36 | 1.29 | 1.09 | 1.05 | 1.03 | 1.02 | 1.00 | 1.00 |
4 | – | – | – | 1.27 | 1.27 | 1.15 | 1.10 | 1.05 | 1.03 | 1.02 |
5 | – | – | – | – | 1.58 | 1.42 | 1.15 | 1.12 | 1.09 | 1.05 |
6 | – | – | – | – | – | 1.43 | 1.38 | 1.18 | 1.15 | 1.10 |
7 | – | – | – | – | – | – | 1.85 | 1.54 | 1.18 | 1.16 |
8 | – | – | – | – | – | – | – | 1.68 | 1.50 | 1.21 |
9 | – | – | – | – | – | – | – | – | 2.14 | 1.66 |
10 | – | – | – | – | – | – | – | – | – | 1.96 |
4. Approximate normal waveforms based on the th order plate theory
Let us construct the waveforms following from the eigenvectors of the operator Eq. (12):
Let us consider the same wavenumber . The exact solution of the three-dimensional problem (e. g. see [34]) known as Goodier and Bisop modes allows one to represent the displacement components as follows:
The normalized exact and approximate waveforms defined by the Eqs. (13), (14) are shown on the Fig. 4.
Fig. 4Normal waveforms of longitudinal modes. Exact solution (solid line), theory of 20th order (○-symbols)
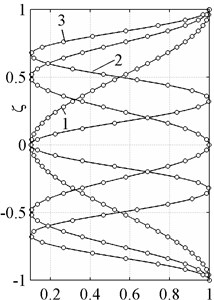
a)
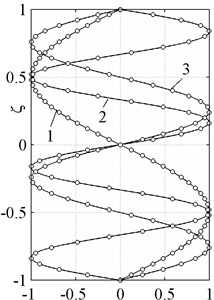
b)
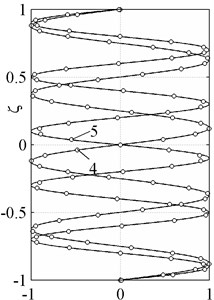
c)
For more details see [37]. Let us consider hence another characteristic point, , corresponding to the Lamé modes.
For the longitudinal waves () we have the following exact solution [34]:
The normalized exact and approximate waveforms corresponding to these modes are shown on the Fig. 5.
Fig. 5Normal waveforms of bending modes. Exact solution (solid line), theory of 20th order (○-symbols)
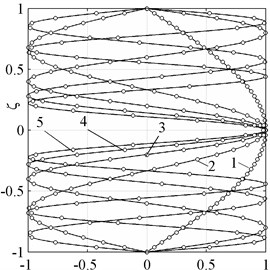
a)
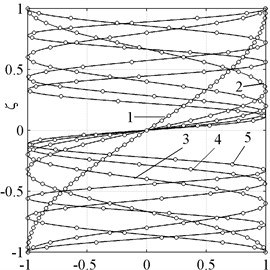
b)
The relative mean square error of the waveform approximation given by the th order plate theory can be introduced as follows [37]:
This error definition will be used below to estimate minimum orders of plate theory that allow one to approximate the exact solution [34].
5. Conclusions
Thus, the convergence of the approximation given by the sequence of solutions based on the plate theories of various orders depends significantly on the wavenumber especially in the phase velocity domain . The phase velocities converge slowly near the point . It can be seen that five lowest phase velocities obtained on the background of the quasi-3D plate theory tends to the dilatation velocity at following plate model’s orders (Table 2).
Table 2Convergence of the 1, 2, …, 5th phase velocities given by the Nth order plate theory: cPhn-c1/c1≤1, κ=πn(β-2-1)1/2
1 | 2 | 3 | 4 | 5 | |
3 | 5 | 7 | 8 | 11 |
The same situation can be observed after constructing the normal waveforms at different nonzero wavenumbers (for more results see [37]).
The convergence of the waveforms computed at the point (Goodier and Bishop modes) as well as at the point (Lamé modes) on the groundwork of the quasi-3D plate theory of th order is estimated by the mean square error , Eq. (16).
Let us define the numerical convergence by the threshold level 0,05 (this depend on the problem, but this level seems to be satisfying in most applications). The minimum model orders allowing one to obtain such a convergence of the waveforms corresponding to the lowest propagating modes are shown in the Table 3.
Table 3Convergence of the 1, 2, …, 5th normal waveforms based on the relative mean square error, Eq. (16): Δαn≤ 0,05
1 | 2 | 3 | 4 | 5 | |
5 | 8 | 12 | 15 | 19 | |
5 | 9 | 13 | 16 | 20 | |
5 | 9 | 13 | 16 | 19 | |
6 | 9 | 12 | 16 | 20 | |
It can be also shown that the relative mean square error of the approximate normal modes become almost stable in the wavenumber domain 15 where is the phase frequency, and can be roughly estimated by the error , [37].
The obtained solution can be useful in the transient waveguide dynamics analysis based on the approximate models. It can be noted that these approximations give the upper estimate of the phase velocities of the normal waves due to the reduced number of degrees of freedom (field variables), but the obtained overestimation depends not only on the model order.
It is shown that the approximate satisfaction of the boundary conditions on the faces in terms of the “elementary” plate theory results in the overestimated longitudinal and bending stiffness especially for the lowest-order models. This drawback can be eliminated on the basis of the “extended” plate theories [33] that allow one to take into account the boundary conditions on the plate faces that are “lost” in the “elementary” theories and to account their effect on the tangent components of the stiffness tensors .
References
-
Grigolyuk E. I., Selezov I. T. Nonclassical Theories of Vibrations of Bars, Plates, and Shells. Results of Science and Engineering, Mechanics of Deformable Solids, Vol. 5, 1973.
-
Brischetto S., Carrera E. Importance of higher order modes and refined theories in free vibration analysis of composite plates. Journal of Applied Mathematics, Vol. 77, Issue 1, 2010, p. 11013.
-
Kienzler R., Altenbach H. Theories of Plates and Shells: Critical Review and New Applications. Springer-Verlag, Berlin, Germany, 2004.
-
Batra R. C., Aimmanee S. Vibrations of thick isotropic plates with higher-order shear and normal deformable plate theories. Computers and Structures, Vol. 83, 2005, p. 934-955.
-
Kang J.-H., Leissa A. W. Three-dimensional vibration analysis of thick, complete conical shells, Transactions of the American Society of Mechanical Engineers, Vol. 71, Issue 6, 2004, p. 502-507.
-
Zozulya V. V., Chang Ch. A high order theory for functionally graded axisymmetric cylindrical shells. International Journal of Mechanical Sciences, Vol. 60, Issue 1, 2012, p. 12-22.
-
Eremeyev V., Pietraszkiewicz W. Refined theories of plates and shells. ZAMM – Journal of Applied Mathematics and Mechanics, Vol. 94, Issues 1-2, 2014, p. 5-6.
-
Pelekh B. L., Lazko V. A. Anisotropic Laminated Plates with Stress Concentrators. Naukova Dumka, Kiev, USSR, 1982.
-
Vekua I. N. Shell Theories: General Methods of Construction. Pitman Advanced Publishing Program, Boston, USA, 1985.
-
ZozulyaV. V. A higher order theory for shells, plates and rods. International Journal of Mechanical Sciences, Vol. 103, 2015, p. 40-54.
-
Zhavoronok S. I. A Vekua-type linear theory of thick elastic shells. ZAMM – Journal of Applied Mathematics and Mechanics, Vol. 94, Issues 1-2, 2014, p. 164-184.
-
Gupta A., Talha M. An assessment of a non-polynomial based higher order shear and normal deformation theory for vibration response of gradient plates with initial geometric imperfections. Composites Part B: Engineering, Vol. 107, Issue 1, 2016, p. 141-161.
-
Gupta A., Talha M., Singh B. N. Vibration characteristics of functionally graded material plate with various boundary constraints using higher order shear deformation theory. Composites Part B: Engineering, Vol. 94, Issue 1, 2016, p. 64-74.
-
Sheikholeslami S. A., Saidi A. R. Vibration analysis of functionally graded rectangular plates resting on elastic foundation using higher-order shear and normal deformable plate theory. Composite Structures, Vol. 106, 2013, p. 350-361.
-
Goldenveizer A. L., Kaplunov J. D. Dynamic boundary layers in problems of vibrations of shells. Mechanics of Solids, Vol. 23, Issue 4, 1988, p. 146-155.
-
Zernov V., Kaplunov J. D. Three-dimensional edge waves in plates. Proceedings of the Royal Society of London A: Mathematics, Physics, and Engineering Sciences, Vol. 464, Issue 2090, 2008, p. 301-318.
-
Wilde M. V. Investigation of the boundary resonance phenomenon in plates on the basis of the 3D elasticity theory equations. Mechanics of Deforming Media, Saratov University, Vol. 16, 2010, p. 7-14.
-
Wilde M. V. Higher order edge waves in thick plates. Vestnik of Lobachevsky University of Nizhni Novgorod, Vol. 9, 2011, p. 173-183.
-
Gorshkov A. G., Medvedskiy A. L., Rabinskiy L. N., Zhavoronok S. I. Plane problems of diffraction of an acoustic pressure wave on a thin orthotropic panel placed in a rigid shield. Mechanics of Solids, Vol. 39, Issue 1, 2004, p. 161-170.
-
Rabinskiy L. N., Zhavoronok S. I. Axisymmetric problem of transient interaction of an acoustical pressure wave with an elastic shell of revolution. Journal of Composite Mechanics and Design, Vol. 12, Issue 4, 2006, p. 541-554.
-
Zhavoronok S. I., Kuprikov M. Yu., Medvedskiy A. L., Rabinskiy L. N. Numerical and Analytical Methods of Solution for Problems of Diffraction of Acoustical Waves on Solids and Shells. Fizmatlit, Moscow, Russia, 2010.
-
Kaplunov J. D., Kossovich L. Yu., Nolde E. V. Dynamics of Thin-Walled Elastic Bodies. Academic Press, 1998.
-
Gordeziani D., Avalishvili M., Avalishvili G. Hierarchical models for elastic shells in curvilinear coordinates. Computers and Mathematics with Applications, Vol. 51, 2006, p. 1789-1808.
-
Schwab C., Wright S. Boundary layers of hierarchical beam and plate models. Journal of Elasticity, Vol. 38, 1995, p. 1-40.
-
Neves A. M. A., Ferreira A. J. M., Carrera E., Cinefra M., Roque C. M. C., Jorge R. M. N., Soares C. M. M. Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Composites Part B: Engineering, Vol. 44, Issue 1, 2013, p. 657-674.
-
Annin B. D., Volchkov Yu M. Nonclassical models of the theory of plates and shells. Journal of Applied Mechanics and Technical Physics, Vol. 57, Issue 5, 2016, p. 769-776.
-
Kienzler R., Schneider P. Consistent theories of isotropic and anisotropic plates. Journal of Theoretical and Applied Mechanics, Vol. 50, Issue 3, 2012, p. 755-768.
-
Zhou D., Au F. T. K., Cheung Y. K., Lo S. H. Three-dimensional vibration analysis of circular and annular plates via the Chebyshev-Ritz method. International Journal of Solids and Structures, Vol. 40, 2003, p. 3089-3105.
-
Volchkov Yu. M., Dergileva L. A. Solving problems for an elastic layer on the basis of approximate equations and comparison with solutions of the elasticity theory. Dynamics of Continuous Media, Institute of Hydrodynamics of Siberian Branch of USSR Academy of Sciences, Novosibirsk, 1977, p. 43-54.
-
Volchkov Yu. M., Dergileva L. A. Reducing three-dimensional elasticity problems to two-dimensional problems by approximating stresses and displacements by Legendre polynomials. Journal of Applied Mechanics and Technical Physics. Vol. 48, Issue 3, 2007, p. 450-459.
-
Zhavoronok S. I. Variational equations of a three-dimensional anisotropic theory of shells. Bulletin of the N. I. Lobachevskiy State University of Nizhny Novgorod, Vol. 4, Issue 5, 2011, p. 2153-2155.
-
Zhavoronok S. I. Variational formulations of Vekua-type shell theories and some their applications. Shell Structures: Theory and Applications, Vol. 3, 2014, p. 341-344.
-
Zhavoronok S. I. On the variational formulation of the extended thick anisotropic shells theory of I.N. Vekua type. Procedia Engineering, Vol. 111, 2015, p. 888-895.
-
Grinchenko V. T., Meleshko V. V. Harmonic Oscillations and Waves in Elastic Bodies. Naukova Dumka, Kiev, 1981.
-
Zhavoronok S. I. Investigation of harmonic waves in elastic layer using Nth order three-dimensional shells’ theory. Journal of Composite Mechanics and Design, Vol. 16, Issue 5, 2010, p. 693-701.
-
Zhavoronok S. I. Investigation of propagating modes of harmonic waves in elastic layer using Nth order three-dimensional shell theory. Journal of Composite Mechanics and Design, Vol. 17, Issue 2, 2011, p. 278-287.
-
Zhavoronok S. I. Kinematics of normal modes in elastic layer for some wavenumbers’ investigation based on Nth order three dimensional shells theory. Journal of Composite Mechanics and Design, Vol. 18, Issue 1, 2012, p. 45-56.
-
Zhavoronok S. I. A formulation of the three-dimensional approximated shells theory of Nth order using generalized displacements and its application to steady dynamics. Journal of Composite Mechanics and Design, Vol. 18, Issue 3, 2012, p. 333-344.
-
Egorova O. V., Kurbatov A. S., Zhavoronok S. I. An application of various Nth order shell theories to normal waves propagation problems. Proceedings of Tula State University, Vol. 11, Issue 1, 2014, p. 255-266.
-
Egorova O. V., Kurbatov A. S., Zhavoronok S. I. The variational equations of the extended Nth order shell theory and its application to some problems of dynamics. Perm National Polytechnic University Mechanics Bulletin, Vol. 2, 2015, p. 36-59.
Cited by
About this article
The investigation was made in Moscow Aviation Institute and supported financially by the Russian Scientific Foundation under Grant No. 14-49-00091-П.
