A multigrid method for EHL line contact problem with Grease as lubricant

1. Introduction

EHL is the study of hydrodynamic lubrication in rolling/sliding contacts when the elastic deformation of the solids is significant. EHL is usually found in many machines parts, for example, gear teeth contacts, cams and rolling element bearings during variations in load etc. EHL problems constitute the following characteristics such as high pressure, deformation of the contacted surfaces and shear rates. The mathematical model of EHL problem depends on a proper fluid rheology model for the lubricant. Many researchers have utilized deliberate methodologies for the numerical solutions of EHL line and point contact problems [1-4]. As most of the roller bearings are lubricated by grease, therefore the EHL equations are solved using grease as a lubricant in order to determine its properties between contacting surfaces. A complete review of EHL theory has been discussed by Lugt et al. [5].

Grease is commonly used as a lubricant in the application of bearing surfaces, it is a choice of lubricant for 80-90 % of bearings. The essential use of grease in bearing components is to ensure long life and low erosion. The main advantage of using grease inherits sealing action; low friction (provided no leakage). The disadvantage of grease is that it has short period compared to other lubricants. Kauzlarich and Greenwood [6] determined experimentally the flow curves for grease which are found to be well correlated with the Herschel-Bulkley model. Wen and Ying [7] examined a hypothetical and test investigation of EHL with thixotropy of grease. Cheng [8] analyzed the influence of pressure and film thickness dispersion in grease EHL, based on its theoretical and numerical analysis in line contact problem using Herschel-Bulkley model for the rheological characteristics of the grease. The effects of thickener structure on film thickness and traction force of lubricating greases in EHL point contact were discussed by Kaneta et al. [9] using optical interferometry technique. Cann and Lubrecht [10] presented the bearing execution limits with grease lubrication, the interaction of bearing design, working conditions and grease properties. Many aspects of grease lubrication have been discussed by Lugt [11]. Cen et al. [12] examined the film thickness of oil greased up contacts at low speeds. The actual operating conditions with an assortment of greases for the accurate prediction of film thickness is of immense importance to ensure controlled separation of contacting surfaces, leading to greater life extent of the mechanical components. In this article we consider an isothermal EHL problem with grease as a lubricant for its film formation, adapting multigrid FAS for its solution.

2. Mathematical formulation

The Herschel-Bulkley model is one of the most important models describing the non-Newtonian rheology of the grease as a lubricant. The model is generally written as $\tau ={\tau }_0+k{\dot{\gamma }}^n$, where $\tau$ is the shear stress, ${\tau }_0$ the yield stress, $\dot{\gamma }$ the shear rate, $n$ the rheological index and $k$is the plastic viscosity. The rheological characteristics of grease depend on the index $n\le$ 1, ${\tau }_0$ and $k$ are functions of pressure and temperature. If $\tau >{\tau }_0$ the Herschel Bulkley model behaves as a fluid, otherwise it behaves as a solid. If $n=$ 1 and ${\tau }_0=$ 0, this model reduces to the Newtonian fluid. For an incompressible, steady and isothermal flow, the modified Reynolds equation governing grease EHL in its dimensionless form is [13]:

where $\xi =\lambda H^{2+1/n}/{\eta }^{1/n}$ and $\lambda =p_H^{1/n}{b}^{2+1/n}/2U\left(2+1/n\right)R^{\left(1+1/n\right)}{2}^{1/n}{\eta }_0^{1/n}$. The non-dimensional parameters for magnitude analysis of Reynolds equation are:

The film thickness at any point on the contacted surface is:

where $H_0$ is the central film thickness, $X^2/2$ defines undeformed contact shape and the integral term represents the elastic deformation of the contact. The non-dimensional viscosity pressure relation given by Roelands [14]:

The equation for applied load in dimensionless form is:

The corresponding boundary conditions are

1) Inlet boundary condition at: $P=$ 0 and.

2) Outlet boundary condition at: $X=X_{out}$, $P=dP/dX=$ 0.

3. Discretization of Reynolds and film thickness equations

The Eq. (1) is discretized using second order finite difference with grid size of $N=$ 32, 64, 128 and the domain of interest is [$X_{in}$, $X_{out}$] = [–2, 1.5]. The discretized form of Reynolds equation is:

where $\delta X=X_i-X_{i-1}$. The discretized form of film thickness Eq. (3) is:

where:

for $i=$ 0, 1, 2, ..., $n$, $j=$ 0, 1, 2, ..., $n$. The force balance equation in discrete form is:

The boundary condition in the inlet $P\left(X_{in}\right)=$ 0 and the boundary in the outlet can be obtained by setting negative pressure equal to zero, the discrete form is:

The convergence criteria for pressure relation is:

where $\epsilon$ is the error.

4. Multigrid method

Multigrid method plays an important role in solving nonlinear mathematical models. Many researchers have developed the generalized ideas in various disciplines underlying multigrid method for the solution of EHL problems. Lubrechet et al. [15] discussed the multigrid method to solve the EHL problem for both line and point contacts which is a significant breakthrough. The efficiency and robustness are improved by eliminating, both high and low-frequency error components by a series of grid with different mesh levels. Venner [16, 17] and Nurgat et al. [18] have introduced new relaxation methods for which the technique was greatly improved. The concept of Multigrid method has been discussed in detail by Briggs et al. [19]. For the solution of a nonlinear system of equations, we use multigrid method with FAS scheme. FAS involve an inner and an outer iteration; the outer iteration is the FAS correction scheme, while the inner iteration is usually a standard relaxation method such as Gauss-Seidel iteration scheme.

4.1. Algorithm (FAS)

The system of nonlinear equations can be written as:

11

$L^h\left(u^h\right)=f^h,$

where $L$ is a nonlinear operator, $u$ is the exact solution, $f$ is a right-hand side function and $h$ is the mesh size of the uniform finer grid ${\mathrm{\Omega }}^h$. Let $v$ be an approximation to the exact solution $u$ then:

$e^h=u^h-v^h\mathrm{}\text{(error)},$

$r^h=f^h-L\left(v^h\right)\text{(residual)}\text{.}$

For simplicity, we consider two grid correction schemes, as follows.

• Applying few number of Gauss-Seidel iteration method on fine grid ${\mathrm{\Omega }}^h$ with initial $v^h$.

• Computation of the restricted residual and restricted current approximation obtained from step 1 (finer to coarser):

$r^{2h}=I_h^{2h}\left(f^h-L^h\left(v^h\right)\right),v^{2h}=I_h^{2h}{v}^h.$

• Solve the problem on coarser grid ${\mathrm{\Omega }}^{2h}$:

$L^{2h}\left(u^{2h}\right)=L^{2h}\left(v^{2h}\right)+r^{2h}.$

• Compute the error approximation of the coarser grid:

$e^{2h}=u^{2h}-v^{2h}.$

• Interpolation of error approximation and correction (coarser to finer):

$v^h\leftarrow v^h+I_{2h}^h{e}^{2h}.$

• Applying few number of Gauss-Seidel iteration method on finer grid ${\mathrm{\Omega }}^h$

The schematic representation of restricted (interpolated) operator from finer grid to coarser grid (coarser grid to finer grid) is shown in the Fig. 1(a, b). The usual multigrid V cycle is shown in the Fig. 2.

Fig. 1a) Restriction, b) interpolation

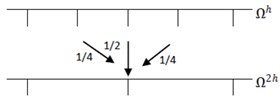
a)

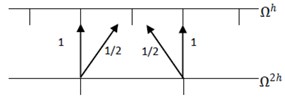
b)

Fig. 2Multigrid V-cycle

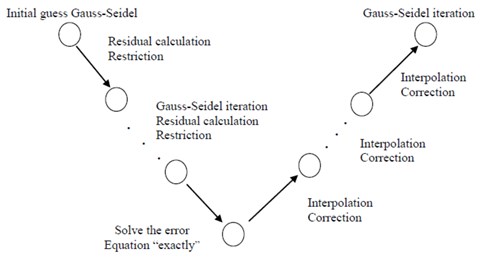
4.2. Method of solution

The process of multigrid method includes the pressure correction and load balance by adjusting the rigid film thickness, which is carried out on the same grid. For an instant, the iteration procedure consists of the pressure iteration and the adjustment for $H_0$. The pressure must be relaxed on each grid level. If we denote ${\left(LP\right)}_i$ by $L_i\left(P\right)$ and ignoring superscripts which represent the grid level, the algebraic equation for pressure on each level can be expressed as: $L_i\left(P\right)=F_i$ ($i=$ 1, 2, ..., $n$-1). For an under-relaxation factor $c_1$, the process for the pressure iteration can be described as [20]:

12

${\tilde{P}}_i={\stackrel{-}{P}}_i+c_1{\delta }_i,$

where:

$\left\{\begin{array}{l}{\delta }_i={\left(\frac{\partial L_i}{\partial P_i}\right)}^{-1}{r}_i,\\ r_i=F_i-\frac{{\xi }_{i+1/2}{\left(P_{i+1}-P_i\right)}^{\frac{1}{n}}-{\xi }_{i-1/2}{\left(P_i-P_{i-1}\right)}^{\frac{1}{n}}}{\delta X^{1+\frac{1}{n}}}+\frac{H_i-H_{i-1}}{\delta X},\\ \frac{\partial L_i}{\partial P_i}=\frac{1}{n}\left[\frac{{\xi }_{i+1/2}{\left(P_{i+1}-P_i\right)}^{1/n}-{\xi }_{i-1/2}{\left(P_i-P_{i-1}\right)}^{1/n}}{\delta X^{1+1/n}}\right]-\left[\frac{\frac{1}{\pi }\left(\stackrel{-}{\rho }{K}_{ij}-{\stackrel{-}{\rho }}_{i-1}{K}_{i-1j}\right)}{\left(\delta X\right)}\right],\end{array}\right.$

and ${\stackrel{-}{P}}_i$, ${\stackrel{-}{P}}_{i+1}$ are initial values of pressure in an iterative process and ${\tilde{P}}_{i-1}$ is the new value of pressure obtained in the iteration. The load balance condition can be achieved by modifying the rigid film thickness ${\stackrel{-}{H}}_0$ as follows:

13

${\stackrel{-}{H}}_0={\tilde{H}}_0+c_1\left[G^{\mathrm{\Delta }}-\frac{\mathrm{\Delta }}{\pi }\sum _{j=1}^{N-1}\left(P_j+P_{j+1}\right)\right],$

where $c_1$ is the relaxation factor and $G^{\mathrm{\Delta }}$ is the non-dimensional load on the coarsest grid. The following procedure is employed to determine the pressure cavitation point is given in Zargari et al. [21]. Let $X_c$ be a point in ($X_{in}$, $X_{out}$), if pressure gradient ${\left.dP/dX\right|}_{X_c}=$ 0, then $X_c$ is the required pressure cavitation point. Otherwise, shift the point $X_c$ on next interval to the left or right depending on ${\left.dP/dX\right|}_{X_c}>$ 0 or ${\left.dP/dX\right|}_{X_c}<$ 0 respectively. Next, approximate another cavitation point ${X_c}^{\text{'}}$ and solve EHL problem. If pressure gradient ${\left.dP/dX\right|}_{{X\text{'}}_c}$ is zero, we get converged solution, otherwise verify the condition:

14

${\left.\frac{dP}{dX}\right|}_{X_c}\times {\left.\frac{dP}{dX}\right|}_{{X\text{'}}_c}<0.$

If the Eq. (14) is not satisfied, repeat above process and find two approximate values $X_c^{\text{'}}$ and $X_c^{\text{'}\text{'}}$ for which Eq. (14) is satisfied. A new cavitation point $X_{new}$ is obtained by interpolating between the two points $X_c^{\text{'}}$ and $X_c^{\text{'}\text{'}}$ which ensures that the pressure gradient nearly equal to zero at $X_{new}$ and results in the required smooth solution of EHL problem.

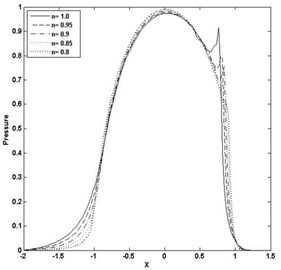
Fig. 3Pressure and film thickness plot for W= 4E-05, U= 5E-11

a)

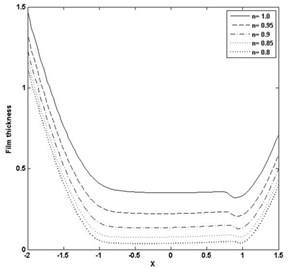
b)

Fig. 4Pressure and film thickness plot for W= 3E-05, U= 2.04E-11

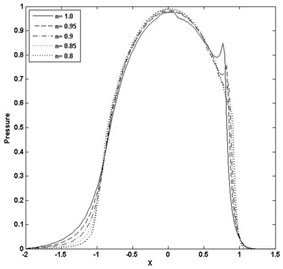
a)

b)

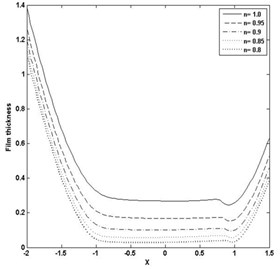
Fig. 5Pressure and film thickness plot for W= 4E-05, U= 5E-11 and n= 0.9

a)

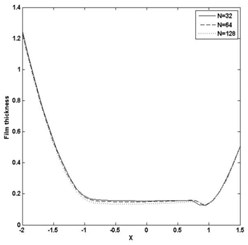
b)

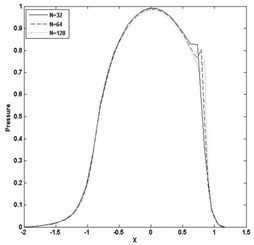
Fig. 6Pressure and film thickness plot for W= 3E-05, U= 2.04E-11 and n= 0.9

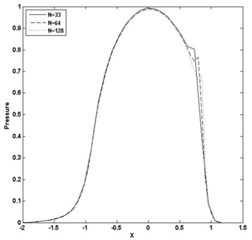
a)

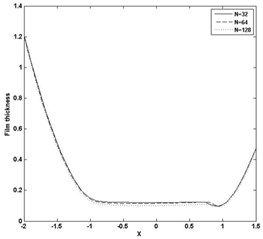
b)

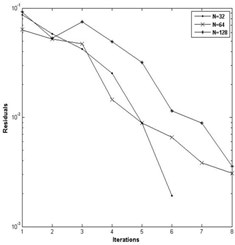
Fig. 7a) Convergence of pressure for W= 4E-05, U= 5E-11 and n= 0.9, b) convergence of pressure for W= 3E-05, U= 2.04E-11 and n= 0.9

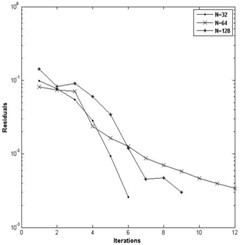
a)

b)

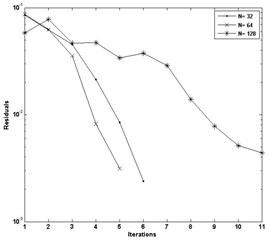
Fig. 8a) Convergence of pressure for W= 4E-05, U= 5E-11 and n= 1.0, b) convergence of pressure for W= 3E-05, U= 2.04E-11 and n= 1.0

a)

b)

5. Results and discussion

The paper presents, the computation of minimum film thickness of grease EHL with different load and speed using multigrid method with FAS, as given in section 4.2. The solution has been calculated on the domain –2.5 < $X$ < 1.5 with different grid size $N$. Table 1 and 2 presents the calculated minimum film thickness for different rheological index ($n$), load ($W$), speed ($U$) and compared with the standard result of Dowson and Higginson [1]. The minimum value of film thickness increases as the index $n$ increases. The pressure profiles have slight variation, corresponding to Newtonian case and pressure spike decreases as index $n$ decreases. Figs. 3 and 4 represents pressure and film thickness profile for different load $W=$ 4E-5, 3E-5, speed $U=$ 5E-11, 2.04E-11, index $n=$ 1.0, 0.95, 0.9, 0.85, 0.8 on the grid size of $N=$ 128. Figs. 5 and 6 represent pressure and film thickness profile for different load ($W$), speed ($U$) taking $n=$ 0.9 over the grid size of $N=$ 32, 64, 128.

The convergence of pressure with different grid over a number of iteration is plotted in the Fig. 7(a, b) for $W=$ 4E-5, 3E-5, $U=$5E-11, 2.04E-11, $n=$ 0.9 and Fig. 8(a, b) for $W=$ 4E-5, 3E-5, $U=$ 5E-11, 2.04E-11, $n=$1.0. In this method the convergence of pressure profile and film thickness is obtained up to $n=$ 0.8. As the mesh points on the finer grid increases, the converging solution decreases. For decrease in the value of index $n$ and increase in the mesh points of finer grid, the pressure spike shrinks and moves toward the outlet.

6. Conclusions

In the present paper, the Reynolds equation and elastic equation is solved to obtain a minimum film thickness of EHL in line contact with grease as a lubricant and can be concluded as: 1) Minimum film thickness increases as the rheological index $n$ increases. 2) Pressure spike decreases as the rheological index $n$ decreases. 3) The advantage of multigrid FAS method incorporates naturally and overcomes the drawbacks of Newton-Raphson scheme.