Abstract
Fault diagnosis for cylindrical roller bearing is of great significance for industry. In order to excavate the features of the vibration signal adequately, and to construct an effective classifier for complex vibration signals, this paper proposed a new fault diagnosis method based on Variational Mode Decomposition (VMD), Singular Value Decomposition (SVD) and Adaboost classifier. Firstly, the VMD was applied to decompose the sampled vibration signal in time-frequency domain. Subsequently, the features were extracted by using SVD. Finally, the constructed Adaboost classifier were employed to fault detection and diagnosis, which were trained by using the extracted features. Experimental data measured in a rotating machinery fault diagnosis experiment platform was used to verify the proposed method. The results demonstrate that the proposed method was effective to detect and diagnose the outer ring fault and rolling element fault in cylindrical roller bearing.
1. Introduction
Cylindrical roller bearing is an important transmission device in industry area, which is yet prone to failure during operation [1]. It is of great significance for the system to operate safely if it can discover the fault and recognize the type of fault accurately in the early stage [2].
Fault diagnosis of cylindrical roller bearing is essentially a pattern recognition process, which mainly includes feature extraction and fault classification [3]. However, it is difficult to extract the characteristic information due to the complex waveform of the vibration signal, which makes it difficult to diagnose the cylindrical roller bearing. In previous studies, different scholars have put forward many methods. In signal decomposition, Local mean decomposition (LMD), Empirical mode decomposition (EMD), Intrinsic time-scale decomposition (ITD) are widely applied [4]. In terms of feature extraction, Principal component analysis (PCA), Multidimensions scaling (MDS), Isomap, Locally Linear Embedding (LLE) are common methods [5-7]. And as for classifier aspects, Bayes, Decision Tree, Support Vector Machine (SVM), K-Nearest Neighbor, etc. are classical algorithm [8-10]. Although the above fault diagnosis methods have been carried out, digging useful information inside the vibration signal based on the analysis of vibration signal has not been fully researched.
In view of the above problem, this paper proposed a fault diagnosis method – VMD-SVD and Adaboost Classifier Method. VMD has been demonstrated of good noise robustness, small sampling effect, and it also has the ability to separate two pure harmonic signals with similar frequencies [11]; SVD has good invariance and stability, which can effectively reduce the random noise in the signal and compress the scale of the fault eigenvector [12]. Adaboost has the advantage of avoiding overfitting, and it has an upper bound of training error rate in Adaboost. All these characteristics represent the good classification ability of the algorithm [13].
The rest of this paper was structured as follows. The second section illustrated the main processes of the proposed method. Experimental investigation of this method was given in third section. The conclusions were given in the fourth section.
2. Methodology
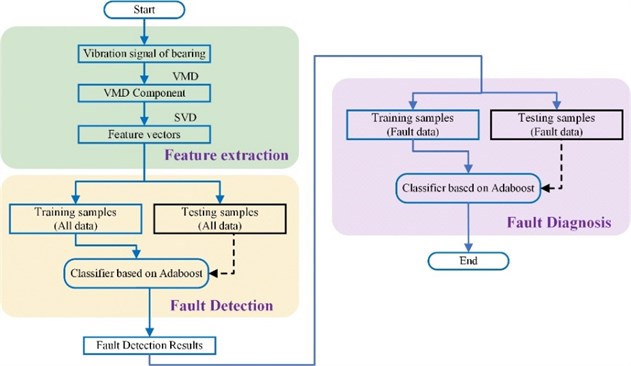
The method proposed in this paper consisted of three main steps, as shown in Fig. 1. The procedures of the method were as follows:
Firstly, the vibration signal of bearing was decomposed in time-frequency domain. The components obtained by VMD were used to construct the component matrix. Then the singular value vector could be obtained by SVD algorithm, and these singular value vectors were regarded as the eigenvectors. Secondly, the eigenvectors were used as training samples to build the classifier. Finally, after the fault detection, the eigenvectors of fault data were used to train another classifier. The fault diagnosis would be completed when all fault data were correctly classified.
Fig. 1The procedures of the proposed methodology
2.1. Signal decomposition by VMD algorithm
VMD is an adaptive signal decomposing method, which can overcome the shortcomings like endpoint effects, modal aliasing as reported in EMD research. Meanwhile, the instantaneous frequency of each basic component by decomposing has its practical meaning in physical.
Its process could be divided into two steps: the establishment part and the solution to the constrained variational problem. The mentioned problem was written as follows:
Subjected to .
In order to transform the constrained variational problem into an unconstrained variational problem, the quadratic penalty and Lagrangian multipliers were introduced to Eq. (1). The augmented Lagrangian was expressed as follows:
The Eq. (2) was solved by iterate search with alternating direction method of multipliers (ADMM).
The mode and the century frequency were written respectively as follows:
2.2. Feature extraction by SVD algorithm
The singular value decomposition theorem and its characteristics can be described as follows:
Theorem: (Singular Value Decomposition Theorem) If (without losing generality, setting ) and , there are two orthogonal matrices:
and a diagonal matrix:
that make the following formula establish, which is:
where the is the eigenvalue of and and , are the eigen vectors of and corresponding to the eigenvalue . The elements on the diagonal of are singular values.
2.3. Pattern recognition by Adaboost classifier
Adaboost is an accurate classifier construction algorithm that the strong learning algorithm is formed by a family of weak learning algorithms through certain rules, which can get a high recognition accuracy of the classified through the sample training. The specific description of the algorithm is as follows:
1) The weak learning algorithm is given and the training set is shown as {(, ), (, ),…, (, )}, where represents the training sample vector and represents the classification mark.
2) The initialized weight is defined as , 1,…, .
3) For 1, 2,…, :
a) The weak learning algorithm is trained under the weight value and the predictive function : can be obtained.
b) The error rate of the predictive function is calculated by:
c) Updating the weights based on the above error rate:
where and is a normalization factor.
d) The final prediction function can be obtained after training:
3. Case study
In order to verify the method proposed in this paper, the rotating machinery fault diagnosis experiment platform of PHM laboratory in Beihang University was used. The cylindrical roller bearing type was N205EM, and the detailed information was shown in Tab. 1. The rolling element fault and outer ring fault were injected by electrospark cutting as shown in Fig. 3. In this paper, the speed was set at 1500 rpm and the sampling frequency was set at 5120 Hz. For each failure mode, the vibration signal data was obtained by continuous sampling for 10 days. In each day, data in 1 s was recorded every 300 s, and totally 102,400 data points of each condition were obtained after 20 sampling in 10 days.
Table 1Structure information of the N205EM bearing
Bearing type | Inner ring diameter | Outer ring diameter | Thickness | Ball type |
N205EM | 25 mm | 52 mm | 15 mm | cylindrical roller |
Fig. 2The schematic of the test-bed

Fig. 3The schematic of failure injection

3.1. Feature extraction based on EMD-SVD
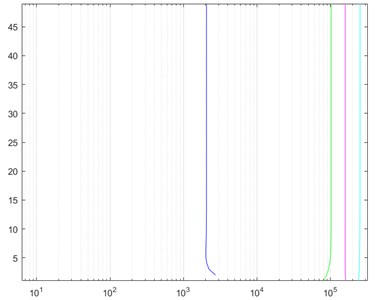
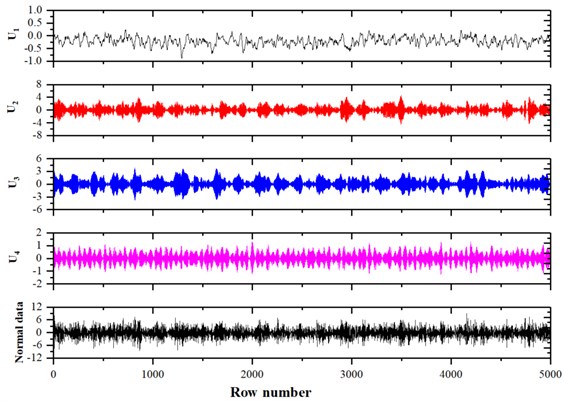
In order to extract the eigenvector of the data sufficiently, we first decomposed the data by VMD in each mode and obtained its components. In this paper, the component number was set to 4, and the center frequency evolution schematic diagram of the component was shown in Fig. 4. The data in normal state and its four components after the decomposition of VMD were shown in Fig. 5. After that, the four components were constructed into a matrix . And then, we took the first 10,000 rows and cut them into 100 matrices in same size (written as ).
Fig. 4Evolution of center frequencies
The singular value vector Vector_SVD4×1 of each matrix Di was obtained by SVD. And the singular value vector was used as the eigenvector, so there were 100 eigenvectors under each condition. Finally, 300 eigenvectors were totally obtained with all the data.
Fig. 5The VMD decomposition diagram of normal data
3.2. State classification based on Adaboost classifier
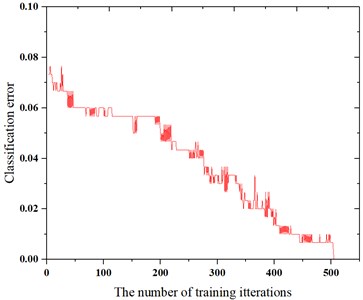
The 300 eigenvectors were entered as training data into the Adaboost classifier. The label value of all eigenvectors extracted from normal data was set to 1, and the other 200 eigenvectors was set to –1. The Adaboost classifier consists of a number of weak classifiers that dynamically adjust threshold values. As can be seen from Fig. 6, with the increase of the number of weak classifiers, the model gradually converged. Finally, a strong classifier was obtained based on these weak classifiers.
Fig. 6Classification error versus number of weak classifier
Because the adaboost classifier in this paper is a binary classifier, the above model could be trained to distinguish normal data from fault data. However, there was no distinction between the rolling element fault and the outer ring fault. Therefore, this paper built another Adaboost classifier in the same way. The training data adopted the eigenvectors of rolling element fault and outer ring fault. In which, the label value of the rolling element fault was set to –1, and the outer ring fault was 1. After training, this classifier could distinguish between these two fault modes.
The accuracy of these classifiers was calculated by classifying the test data. By entering 300 samples (including 100 normal samples, 100 outer ring fault samples, and 100 scroll-fault samples) into the constructed classifier, the fault detection rate of distinguishing between normal data and fault data was 97 % and the fault diagnosis rate of distinguishing between the fault modes was 95 %. The results showed that the method proposed in this paper was practical and effective for fault diagnosis of cylindrical roller bearing.
4. Conclusions
In order to solve the problem of cylindrical roller bearing fault diagnosis, this paper proposed a fault diagnosis method. To extract useful information from the signal better, the signal was first decomposed by VMD and then the eigenvectors of the data were extracted by SVD. Finally, the Adaboost classifier was obtained by training. After experimental verification, the proposed method had high robustness and was effective and feasible for fault diagnosis of cylindrical roller bearing.
References
-
Leblanc A., Nelias D., Defaye C. Nonlinear dynamic analysis of cylindrical roller bearing with flexible rings. Journal of Sound and Vibration, Vol. 325, Issues 1-2, 2009, p. 145-160.
-
Frank P. M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: a survey and some new results. Automatica, Vol. 26, Issue 3, 1990, p. 459-474.
-
Kawai T., Akira S. The role of pattern-recognition receptors in innate immunity: update on Toll-like receptors. Nature Immunology, Vol. 11, Issue 5, 2010, p. 373-384.
-
Wang Y., He Z., Zi Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis. Journal of Vibration and Acoustics-transactions of the ASME, Vol. 132, Issue 2, 2010, p. 613-624.
-
Li R. Y., Rong G. Principal component analysis (PCA) of fault isolation based on fault mapping vector and structured residual. Control Theory and Applications, Vol. 25, Issue 6, 2008, p. 1099-1104.
-
Bengio Y., Paiement J. F., Vincent P. Out-of-sample extensions for LLE, Isomap. Advances in Neural Information Processing Systems, Vol. 16, 2004, p. 177-184.
-
Ziegel E. R. Fault detection and diagnosis in industrial systems. Advanced Textbooks in Control and Signal Processing, Vol. 12, Issue 3, 2002, p. 453-454.
-
Landgrebe D. A survey of decision tree classifier methodology. IEEE Transactions on Systems Man and Cybernetics, Vol. 21, Issue 3, 2002, p. 660-674.
-
Cherkassky V., Ma Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Networks, Vol. 17, Issue 1, 2004, p. 113-126.
-
Khakzad N., Khan F., Amyotte P. Safety analysis in process facilities: comparison of fault tree and Bayesian network approaches. Reliability Engineering and System Safety, Vol. 96, Issue 8, 2011, p. 925-932.
-
Mohanty S., Gupta K. K., Raju K. S. Comparative study between VMD and EMD in bearing fault diagnosis International Conference on Industrial and Information Systems, 2015.
-
Liu H., Wang X., Lu C. Rolling bearing fault diagnosis under variable conditions using Hilbert-Huang transform and singular value decomposition. Mathematical Problems in Engineering, Vol. 2014, 2014, p. 765621.
-
Martin Diaz I., Morinigo Sotelo D., Duque Perez O., et al. Early fault detection in induction motors using Adaboost with imbalanced small data and optimized sampling. IEEE Transactions on Industry Applications, Vol. 53, Issue 3, 2017, p. 3066-3075.
About this article
This study is supported by the Fundamental Research Funds for the Central Universities (Grant No. YWF-17-BJ-J-42 and YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51605014 and 51575021), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
