Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount

Nguyen, Van Liem; Nguyen, Khac Tuan

doi:10.21595/vp.2018.20339

Vibroengineering Procedia

Browse Procedia

Published: 13 December 2018

Check for updates

Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount

Van Liem Nguyen¹

Khac Tuan Nguyen²

^{1, 2}Hubei Polytechnic University, Huangshi City, China

^{1, 2}Thai Nguyen University of Technology, Thai Nguyen City, Vietnam

Corresponding Author:

Khac Tuan Nguyen

Cite the article Download PDF

Downloads 1357

CrossRef Citations 6

Abstract

In order to improve the vibratory roller’s ride comfort, a 3-D nonlinear dynamic model of the vehicle interacting with the off-road terrain is established. A damper hydraulic mount is studied and combined with the cab’s rubber mounts to simulate and evaluate the performance of the ride comfort. The weighted RMS acceleration responses of the vertical driver’s seat, the cab’s pitch and roll angle are chosen as objective functions. The results show that the cab’s rubber mounts combined with the damper hydraulic mount are clearly improved the ride comfort under various operating conditions. Especially, with damping coefficients $c_{c 3,4} =$ 1.8 kN.s.m^-1, the weighted RMS values of the vertical driver’s seat, the cab’s pitch and roll angle are greatly reduced by 27.8 %, 22.7 % and 64.3 % in condition of the vehicle traveling, and by 23.8 %, 20.0 % and 63.7 % in condition of the vehicle compacting on an elastic-plastic terrain.

Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount

Highlights

Vibratory roller, cab's isolation mounts, ride comfort
Vehicle dynamic model
Off-road terrain, deformable terrain

1. Introduction

The off-road vibratory roller is a compactor which often uses in the field of the construction site, factories, etc. Its operating principle is the combination of the static force of the vehicle and the dynamic force of the drum to compact soil ground, asphalt and other materials. Thus, designers always want the excitation force of the drum to achieve the maximum value, whereas vibrations are transmitted from the drum/tires through the vibration isolation systems into the cab floor and the driver’s seat to achieve the minimum value. Almost the vibratory roller is not equipped with the suspension system to link between the chassis and the axles, so the vibration sources impact to the driver via the cab’s isolation system and driver’s seat suspension. Thus, the cab’s isolation system is one of the most important factors to improve the vehicle ride comfort.

Basic researches of the tire-deformable soil interaction [1-3], of the rigid drum and elastic-plastic soil interaction [4] indicated that the vibration responses of the vehicle are greatly influenced by off-road terrain. Almost the vehicle cab is always equipped with the rubber mounts with high stiffness characteristic and low damping of rubber material [5-7]. Therefore, the stiff rubber property helps suppress only high-frequency vibration and noise, contrariwise, the low damping of the natural rubber generates the high magnitude vibrations which can reduce the vehicle’s ride comfort [6]. The influence of design parameters of the cab’s rubber mounts on the ride comfort was analyzed [5], the parameters of the cab’s rubber mounts were then optimized to increase the ride comfort [7]. The results showed that the vehicle’s ride comfort was improved. However, the vibrations of the vertical driver’s seat and the cab’s pitch angle are still great under operation conditions.

In order to improve the driver’s ride comfort and controlling the cab shaking of the vehicle. A dynamic model of the vibratory roller is established based on the elastic-plastic soil model [4] and the hypothesis of the soft soil model [1]. The cab’s rubber system is then added by the damper hydraulic mounts to analyze the performance of the ride comfort. The vibration excitations consist of the interactions of the drum/tires-terrain roughness surface when the vehicle travels on a soft soil and an excitation frequency 28 Hz of the drum when the vehicle compacts on the elastic-plastic soil. The performance of the ride comfort is evaluated through the weighted root-mean-square (RMS) acceleration responses of the vertical driver’s seat ( $a_{w s}$ ), the cab’s pitch ( $a_{w ϕ c}$ ) and roll ( $a_{w θ c}$ ) angle under operation conditions.

2. Off-road vehicle model

2.1. Vibratory roller dynamic model

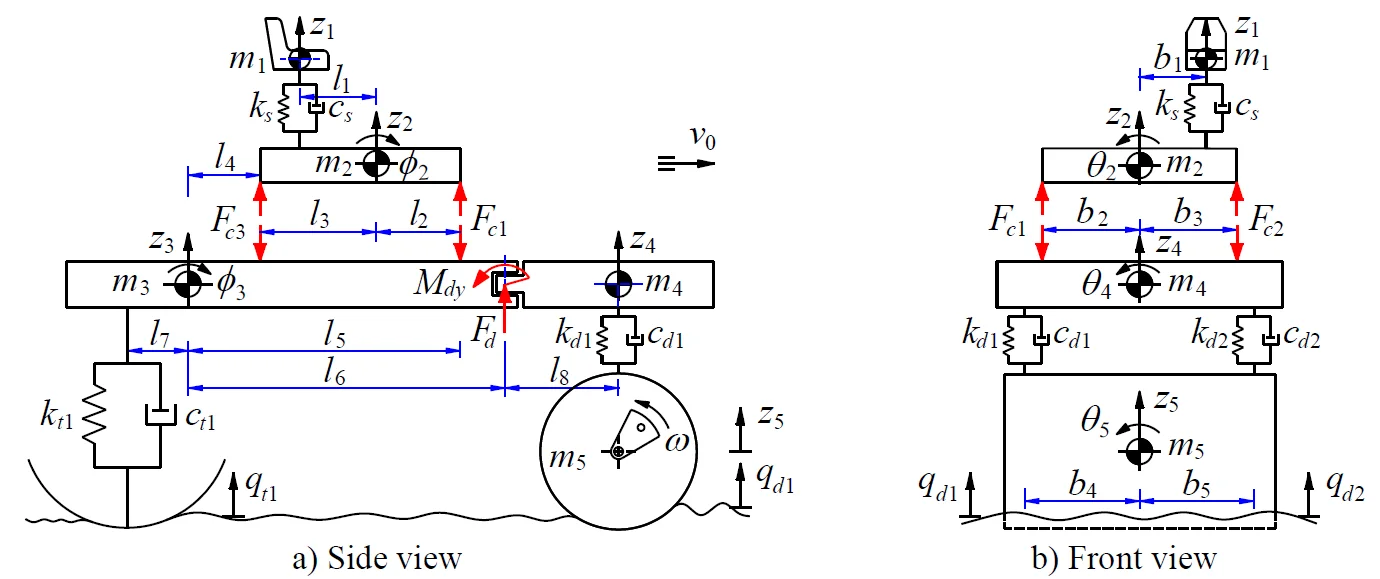
A 3-D nonlinear dynamic model of an off-road vibratory roller with 9 degrees of freedom (DOF) considering the interaction between wheels and off-road terrains is established to analyze the performance of cab’s isolation system, as shown in Fig. 1.

In Fig. 1, $z_{v}$ and $m_{v}$ are the vertical displacements and masses at centre of gravity of the driver’s seat, the cab, the rear/front vehicle frame and the drum; $ϕ_{2,3}$ and $θ_{j}$ are the angular displacements at centre of gravity of the cab, the rear/front vehicle frame and the drum; $k_{s}$ , $k_{d 1,2}$ , $k_{t 1,2}$ and $c_{s}$ , $c_{d 1,2}$ , $c_{t 1,2}$ are the stiffness and damping coefficients of the driver’s seat suspension, the drum’s rubber mounts and tires; $F_{c i}$ are the dynamic reaction forces of the cab’s isolation mounts; $q_{d 1,2}$ and $q_{t 1,2}$ are the excitations of the off-road terrains; $l_{u}$ and $b_{v}$ is the distances of the vehicle ( $i =$ 1-4; $j =$ 2-5; $u =$ 1-8; $v =$ 1-5).

Based on the vehicle dynamic model in Fig. 1, and by applying Newton’s second law of motion, the motion equations of the vehicle can be represented in the matrix form as follows:

1

[M] \{\ddot{Z}\} + [C] \{\dot{Z}\} + [K] \{Z\} = \{F (t)\},

where [ $M$ ], [ $C$ ] and [ $K$ ] are ( $m$ × $m$ ) mass, damping and stiffness matrices, respectively, { $Z$ } is the ( $m$ ×1) displacement vector, { $F (t)$ } is the ( $m$ ×1) exciting force vector, and $m$ is the number of DOF., ( $m =$ 9).

Fig. 13D dynamic model of an off-road vibratory roller with cab’s isolation system

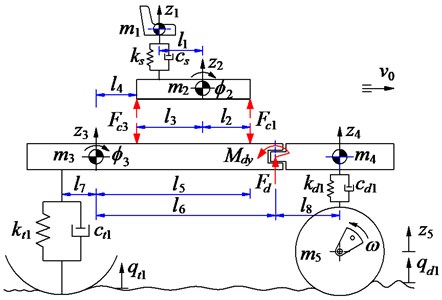
a) Side view

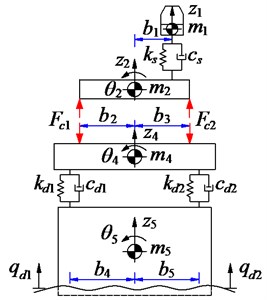
b) Front view

2.2. Cab’s vibration isolation system model

The lumped parameter model of the cab’s isolation system is described as in Fig. 2(a). Herein, $k_{r}$ and $c_{r}$ are the linear stiffness and damping coefficient of the rubber mount, $c_{h}$ is the damping coefficient of the hydraulic mount which is added in the cab’s isolation system.

The corresponding dynamic force of the mount $i$ of the cab’s isolation mounts is given by:

2

F_{c i} = \{\begin{array}{l} k_{r i} (z_{2 i} - z_{3 i}) + c_{r i} ({\dot{z}}_{2 i} - {\dot{z}}_{3 i}), Without damper hydraulic mount, \\ k_{r i} (z_{2 i} - z_{3 i}) + (c_{r i} + c_{h i}) ({\dot{z}}_{2 i} - {\dot{z}}_{3 i}), With damper hydraulic mount, \end{array}

where ( ${\dot{z}}_{2 i}$ , ${\dot{z}}_{3 i}$ ) and ( $z_{2 i}$ , $z_{3 i}$ ) are the relative velocities and the displacements of the cab floor and the rear vehicle frame at the mount $i$ and there are given by:

3

z_{2 i} = z_{2} + (- 1)^{α} l_{α + 1} ϕ_{2} + (- 1)^{i} b_{δ} θ_{2}, {\dot{z}}_{2 i} = {\dot{z}}_{2} + (- 1)^{α} l_{α + 1} {\dot{ϕ}}_{2} + (- 1)^{i} b_{δ} {\dot{θ}}_{2},

4

z_{3 i} = z_{3} - l_{υ} ϕ_{3} + (- 1)^{i} b_{δ} θ_{3}, {\dot{z}}_{3 i} = {\dot{z}}_{3} - l_{υ} {\dot{ϕ}}_{3} + (- 1)^{i} b_{δ} {\dot{θ}}_{3},

where $i =$ 1, 2 then $α =$ 1, $υ =$ 5 and $δ =$ $i +$ 1, and $i =$ 3, 4 then $α =$ 2, $υ =$ 4 and $δ = i -$ 1.

Fig. 2The exciting forces models of cab’s isolation system, the tires and the drum

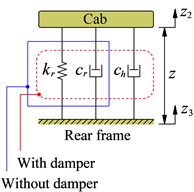
a) Cab’s isolation system

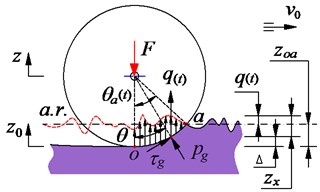
b) Wheel-deformable soil interaction

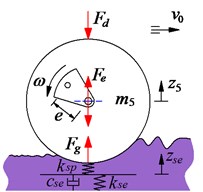
c) Drum and elastic-plastic interaction

2.3. Dynamic off-road vehicle and deformable soil interaction models

2.3.1. The wheels-deformable soil contact model

The vibratory roller travels on the deformable terrain into the workshop, the drum/tires-deformable soil contact model with the terrain roughness surface is investigated based on the traditional model of Bakker and Wong [1, 2]. The wheel moves on a random terrain surface $q (t)$ of deformable terrain, under the effect of the static and dynamic loads of the wheel, the terrain is then sunk $z_{o a}$ , as seen in Fig. 2(b). The pressure $p_{g}$ and the shear stress $τ_{g}$ arising from the soil compression in the deformable area region (arc of $o a$ ) thus impact contrary on the wheel. Consequently, the reaction force $F_{g}$ of the soil under the wheel is given by:

5

F_{g} = \int_{0}^{θ_{a} (t)} B p_{g} r c o s θ d θ + \int_{0}^{θ_{a} (t)} B τ_{g} r s i n θ d θ .

The $p_{g}$ and $τ_{g}$ were given by Bakker [1] as follows:

6

p_{g} = (\frac{k_{c}}{b} + k_{φ}) z_{x}^{n}, τ_{g} = (c + p_{g} t a n φ) (1 - e^{- \frac{j_{d}}{K}}) .

Assuming $a$ . $r$ . is the average roughness line of the terrain surface, thus, the sinking of the soil $z_{x}$ can be determined by $z_{x} = q (t) + z_{o a} - ∆$ , herein, $q (t)$ is the random excitation of the off-road terrain surface and it is described as follows:

The ride comfort of the vibratory roller is strongly influenced not only by wheels-deformable terrain interaction but also by the rough terrain surfaces $q (t)$ . Therefore, the spectral density of the off-road terrain surface is written in accordance with the ISO proposal [8] over the different spatial frequency ranges by $S (Ω) = S (Ω_{0}) . (Ω / Ω_{0})^{- w_{0}}$ . Herein, $w_{0} =$ 3 for $Ω \leq Ω_{0}$ and $w_{0} =$ 2.25 for $Ω > Ω_{0}$ , the value $S (Ω_{0})$ provides a measure for the random terrain with the reference spatial frequency $Ω_{0} =$ 1/2 $π$ (cycle.m^-1).

More specifically, assuming the vehicle travels with a constant speed $v_{0}$ , the off-road terrain irregularities can be simulated by the series:

7

q (t) = \sum_{i = 1}^{N} s_{i} \sin (i Δ ω t + φ_{i}),

where $N$ is the number of intervals, $s_{i} = \sqrt{2 S (i Δ n) Δ n}$ is the amplitude of each the excitation harmonic in which S is the target spectral density, $Δ n = 2 π / L$ and $L$ is the length of the road segment, $φ_{i}$ is a random phase uniformly distributed between 0 and 2 $π$ , and $Δ ω = Δ n v_{0}$ is the fundamental temporal frequency. Mitschke [3] extended the spectral density ranges for the unpaved off-road classifications apart from the traditional asphalt road classifications, including the classification ranges from good to very poor, and the desired terrain roughness can be yielded by choosing a value in the spectral density ranges.

According to the dynamic model of the vibratory roller in Fig. 1 and the wheels-soft terrain interaction model in Fig. 2(b), the excitation forces $F_{t}$ and $F_{d}$ of the wheels and the drum from the deformable terrain to the rear/front vehicle frame are described by Eq. (8) and Eq. (9):

8

\{\begin{array}{l} F_{t j} + F_{g j} - m_{t j} g = 0, \\ F_{t j} = k_{t} (z_{3} - l_{7} ϕ_{3} - z_{t}) + c_{t} ({\dot{z}}_{3} - l_{7} {\dot{ϕ}}_{3} - {\dot{z}}_{t}), \end{array}

9

\{\begin{array}{l} m_{5} {\ddot{z}}_{5} = F_{d j} - F_{g j} + m_{5} g, \\ F_{d j} = k_{d} (z_{4} - z_{5}) + c_{d} ({\dot{z}}_{4} - {\dot{z}}_{5}), j = 1,2 . \end{array}

2.3.2. The rigid drum and elastic-plastic soil interaction model

The vibratory roller uses the most of its time to work on the workshop which often operates under the elastic-plastic soil. Therefore, according to Adam and Kop [4], a model of the rigid drum and elastic-plastic soil contact is established in Fig. 2(c), the elastic-plastic property can be expressed by a plasticity factor $ε$ and a soil damping to plasticity ratio $γ$ as following:

10

ε = \frac{k_{s p}}{k_{s p} + k_{s e}}, γ = \frac{c_{s e}}{k_{s p}},

where $ε$ is the compression ratio, $k_{s e}$ is the elastic stiffness, $k_{s p}$ is the compression stiffness, $c_{s e}$ is the compression damper.

In an exciting vibration cycle of the drum-deformed soil contact, the motion of the vibratory drum on a soil patch of given density may exhibit, over each cycle of the vibratory drum, two or more often three distinct phases, which are described as follows: (1) Loading Phase: The gravel-soil ground is compressed by the drum, thus, the gravel-soil ground density is increased and it has become elasticity. The elastic stiffness and compression stiffness of the gravel-soil ground are increased while the compression damper is decreased. In order to describe the relation of $z_{5}$ , $ε$ and $γ$ , the vibration equation of the drum is given by Eq. (11) [5]; (2) Unloading Phase: The roller drum moves upward, the gravel-soil ground is restored. The vibration equation of the drum is written by Eq. (12); and (3) Drum-Hope Phase: The gravel-soil ground has become elasticity, the drum is easy to separate from the soil ground surface, and the vibration equation is also written by Eq. (13):

11

\{\begin{array}{l} ε γ m_{5} {\overset{⃛}{z}}_{5} + m_{5} {\ddot{z}}_{5} = ε γ {\dot{F}}_{d} + F_{d} - ε c_{s e} {\dot{z}}_{5} + (ε - 1) k_{s p} z_{5} \\ + ε γ m {}_{e} e ω^{3} c o s ω t + m_{e} e ω^{2} s i n ω t, \\ F_{d j} = k_{d j} [z_{4} - z_{5} + (- 1)^{j} b_{j + 3} (θ_{4} - θ_{5})] + c_{d j} [{\dot{z}}_{4} - {\dot{z}}_{5} + (- 1)^{j} b_{j + 3} ({\dot{θ}}_{4} - {\dot{θ}}_{5})], \end{array}

12

m_{5} {\ddot{z}}_{5} = F_{d j} - c_{s e} {\dot{z}}_{5} + m_{e} e ω^{2} s i n ω t,

13

m_{5} {\ddot{z}}_{5} = F_{d j} + m g + m_{e} e ω^{2} s i n ω t, j = 1,2 .

From Eqs. (11)-(13), the motion of the drum $z_{5}$ and the excitation forces $F_{d}$ is then determined.

3. Results and discussion

3.1. The off-road vehicle travels to the workshop

The effect of the damping coefficients to the vehicle ride comfort is evaluated through the evaluate indices of the weighted RMS acceleration responses ( $a_{w z}$ ) in ISO 2631-1 (1997) [9]. In a condition of the vehicle traveling into the workshop, the reference parameters of a vibratory roller [6] and a Grenville SAND deformation with its poor off-road classification $q (t)$ [3] are used to simulate at a vehicle velocity of $v_{0} =$ 2.22 m.s^-1 (8 km.h^-1). Assuming the initial damping coefficients of the damper hydraulic mounts are $c_{0} =$ 1.5 kN.s.m^-1. The damping coefficients $c_{c i} = {[0.2,0.4, \dots, 2.0]}^{T} \times c_{0}$ with three different cases $c_{c i} = {[c_{c 1,2}, c_{c 3,4}, c_{c 1,2, 3,4}]}^{T}$ of the mount $i$ are simulated, as seen in Fig. 4. The results show that the weighted RMS acceleration responses of the driver’s seat ( $a_{w s}$ ), the cab’s pitch and roll angle ( $a_{w ϕ c}$ and $a_{w θ c}$ ) are lightly affected by the damping coefficients $c_{c 1,2}$ of the front-end mounts, whereas these values are strongly affected by the damping coefficients $c_{c 3,4}$ of the rear-end mounts and $c_{c 1,2, 3,4}$ of all mounts $i$ . However, the effect of all $c_{c 1,2, 3,4}$ to the ride comfort is insignificant in comparison with $c_{c 3,4}$ of rear-end mounts, therefore, the values $c_{c 3,4}$ are chosen to analyze the results. Fig. 4(a), (b) and (c) show that $0.2 \times c_{0} \leq c_{c 3,4} < 1.0 \times c_{0},$ all values of $a_{w s},$ $a_{w ϕ c}$ and $a_{w θ c}$ are strongly reduced; $1.0 \times c_{0} < c_{c 3,4} \leq 2.0 \times c_{0},$ both values of $a_{w ϕ c}$ and $a_{w θ c}$ are greatly reduced, especially $1.2 \times c_{0} \leq c_{c 3,4}$ , however, the value of $a_{w s}$ is enhanced. It implies that the comfortable shake of the driver is enhanced while the vertical driver’s ride comfort is decreased. The minimum value of $a_{w s}$ is obtained in a range of $0.8 \times c_{0} < c_{c 3,4} \leq 1.4 \times c_{0}$ (see Fig. 4(a)). In order to improve the ride comfort in all directions, the values of $c_{c 3,4}$ could be chosen in a range of $1.0 \times c_{0} < c_{c 3,4} \leq 1.4 \times c_{0}$ . With the values of $c_{c i}$ is chosen by $c_{c 3,4} = 1.2 \times c_{0} =$ 1.8 kN.s.m^-1 and $c_{c 1,2} = 1.0 \times c_{0} =$ 1.5 kN.s.m^-1, the simulation results is plotted in Fig. 5. The results show that the acceleration responses of the driver’s seat, the cab’s pitch and roll angle are significantly reduced in comparison with the cab’s isolation system without the damper hydraulic mounts. The weighted RMS values of $a_{w s}$ , $a_{w ϕ c}$ and $a_{w θ c}$ in Table 1 are clearly decreased by 27.8 %, 22.7 % and 64.3 % in comparison with the cab’s isolation system without the damper hydraulic mounts.

Fig. 4Effect of the damper coefficients to the ride comfort on a deformable soil ground

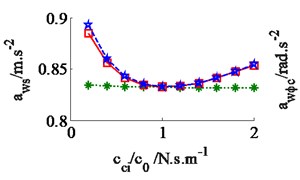
a) The vertical driver’s seat

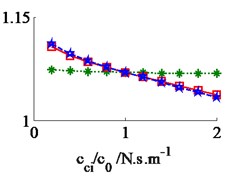
b) The cab’s pitch angle

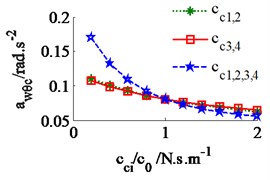
c) The cab’s roll angle

Fig. 5The acceleration responses of the driver’s seat and the cab on a deformable soil ground

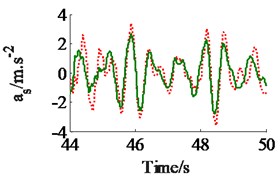
a) The vertical driver’s seat

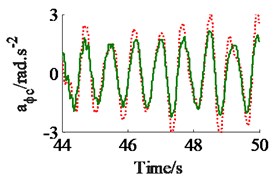
b) The cab’s pitch angle

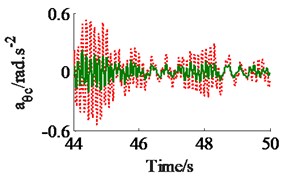
c) The cab’s roll angle

Table 1Weighted RMS values of the driver’s seat and cab on a deformable soil ground

Parameters	$a_{w s}$ m.s^-2	$a_{w ϕ c}$ rad.s^-2	$a_{w θ c}$ rad.s^-2
Without damper	1.15	1.36	0.202
With damper	0.83	1.05	0.072
Reduction (%)	27.8 %	22.7 %	64.3 %

Table 2Weighted RMS values of the driver’s seat and cab on an elastic-plastic soil ground

Parameters	$a_{w s}$ m.s^-2	$a_{w ϕ c}$ rad.s^-2	$a_{w θ c}$ rad.s^-2
Without damper	0.88	0.50	0.323
With damper	0.67	0.40	0.117
Reduction (%)	23.8 %	20.0 %	63.7 %

3.2. The off-road vehicle works in the workshop

In a condition of the vehicle working in the workshop, a low-density soil of elastic-plastic soil [4] with a vehicle velocity of $v_{0} =$ 1.38 m.s^-1 (5 km.h^-1) and under an exciting frequency, 28 Hz, of the drum are chosen to analyze the ride comfort. It is also assumed that the initial damping coefficients of the damper hydraulic mounts are $c_{0} =$ 1.5 kN.s.m^-1. The simulation results in Fig. 6 show that the effect of the damping coefficients in cases of $c_{c 1,2}$ , $c_{c 3,4}$ , and $c_{c 1,2, 3,4}$ is also similar in a condition of the vehicle traveling. Thus, the values c_c_3,4 are also chosen to analyze the results. Fig. 6(a) and (c) show that $0.2 \times c_{0} \leq c_{c 3,4} \leq 2.0 \times c_{0}$ , both the value of $a_{w s}$ and $a_{w θ c}$ are clearly decreased; Fig. 6(b) shows that $0.2 \times c_{0} < c_{c 3,4} \leq 1.2 \times c_{0}$ , the value $a_{w ϕ c}$ is also reduced, however, $1.2 \times c_{0} < c_{c 3,4} \leq 2.0 \times c_{0}$ , the value $a_{w ϕ c}$ is significantly enhanced. Therefore, in order to improve the ride comfort in all directions, the values of $c_{c 3,4}$ could be chosen in a range of $1.0 \times c_{0} < c_{c 3,4} \leq 1.4 \times c_{0} .$ With the values of $c_{c i}$ is also chosen by $c_{c 3,4} = 1.2 \times c_{0} =$ 1.8 kN.s.m^-1 and $c_{c 1,2} = 1.0 \times c_{0} =$ 1.5 kN.s.m^-1, the simulation results is seen in Fig. 7. The results show that the acceleration responses are significantly reduced in comparison with the cab’s rubber mounts. The weighted RMS values of $a_{w s}$ , $a_{w ϕ c}$ and $a_{w θ c}$ in Table 2 are also reduced by 23.8 %, 20.0 % and 63.7 % in comparison with the cab’s isolation system without the damper hydraulic mounts.

Fig. 6Effect of the damper coefficients to the ride comfort on an elastic-plastic soil ground

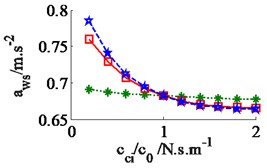
a) The vertical driver’s seat

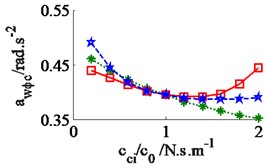
b) The cab’s pitch angle

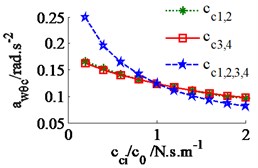
c) The cab’s roll angle

Fig. 7The acceleration responses of the driver’s seat and cab on an elastic-plastic soil ground

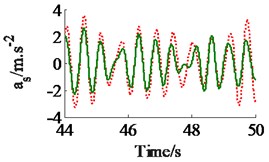
a) The vertical driver’s seat

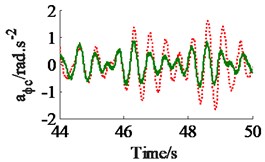
b) The cab’s pitch angle

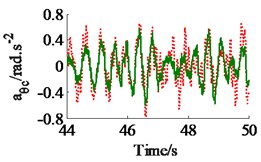
c) The cab’s roll angle

4. Conclusions

The ride comfort performance of the off-road vibratory roller cab’s isolation system added the damper hydraulic mount is clearly improved under operating conditions. Especially, (1) In a condition of the vehicle traveling, with $c_{c 1,2} =$ 1.5 kN.s.m^-1 and $c_{c 3,4} =$ 1.8 kN.s.m^-1, the weighted RMS values of $a_{w s}$ , $a_{w ϕ c}$ and $a_{w θ c}$ are significantly reduced by 27.8 %, 22.7 % and 64.3 % in comparison with the cab’s isolation system without the damper hydraulic mounts. (2) In a condition of the vehicle compacting, with $c_{c 1,2} =$ 1.5 kN.s.m^-1 and $c_{c 3,4} =$ 1.8 kN.s.m^-1, the weighted RMS values of $a_{w s}$ , $a_{w ϕ c}$ and $a_{w θ c}$ are significantly reduced by 23.8 %, 20.0 % and 63.7 % in comparison with the cab’s isolation system without the damper hydraulic mounts.

References

Bekker M. Introduction to Terrain-Vehicle Systems. University of Michigan Press, Ann Arbor, 1969.

Search CrossRef
Wong J. Theory of Ground Vehicles. John Wiley and Sons Inc, New York, 2001.

Search CrossRef
Mitschke M. Dynamik Der Kraftfahrzeuge. Springer-Verlag, Berlin, 1972.

Publisher
Adam D., Kopf F. Theoretical analysis of dynamically loaded soils. European Workshop Compaction of Soils and Granular Materials, Paris, 2000, p. 207-220.

Search CrossRef
Kordestani A., Rakheja S., Marcotte P., Pazooki A., Juras D. Analysis of ride vibration environment of soil compactors. International Journal of Commercial Vehicles, Vol. 3, Issue 1, 2010, p. 259-272.

Publisher
Van Liem N., Jianrun Z., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 1-12.

Publisher
Le V. Q., Nguyen K. T. Optimal design parameters of cab’s isolation system for vibratory roller using a multi-objective genetic algorithm. Applied Mechanics and Materials, Vol. 875, 2017, p. 105-112.

Publisher
SO/TC108/SC2/WG4 N57, Reporting Vehicle Road Surface Irregularities, 1982.

Search CrossRef
ISO 2631-1. Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole Body Vibration-Part 1: General Requirements, 1997.

Search CrossRef

Cited by

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li | Vanliem Nguyen | Xiaoyan Guo | Yan Kang

(2021)

Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

Yan Kang | Vanliem Nguyen | Xiaoyan Guo | Yuehan Li

(2021)

Study to control the cab shaking of vibratory rollers using the horizontal auxiliary damping mount

Vanliem Nguyen | Renqiang Jiao | Vanquynh Le | Peiling Wang

(2020)

Effect of the mass-stiffness distribution of the vibratory roller cab on the ride quality in low-frequency region

Huan Yuan | Zhiqiang Zhang | Aoran Yang | Hao Dong

(2020)

2019 6th International Conference on Systems and Informatics (ICSAI)

Beiping Zhang | Nguyen Van Liem

(2019)

Performance of PID-Fuzzy control for cab isolation mounts of soil compactors

Vanliem Nguyen | Renqiang Jiao | Vanquynh Le | Anhtan Hoang

(2019)

About this article

Received

23 October 2018

Accepted

31 October 2018

Published

13 December 2018

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/vp.2018.20339

Keywords

off-road vibratory roller

cab’s rubber system

damper hydraulic mount

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 02 16

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li, Vanliem Nguyen, Xiaoyan Guo, Yan Kang

Research article

2021 02 05

Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

Yan Kang, Vanliem Nguyen, Xiaoyan Guo, Yuehan Li

Research article

2020 11 26

Effect of the mass-stiffness distribution of the vibratory roller cab on the ride quality in low-frequency region

Huan Yuan, Zhiqiang Zhang, Aoran Yang, Hao Dong

Research article

2020 06 30

Development of cab isolation systems of off-road vibratory rollers: review research

Vanliem Nguyen, Vanquynh Le

V. L. Nguyen and K. T. Nguyen, “Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount,” Vibroengineering PROCEDIA, Vol. 21, pp. 89–95, Dec. 2018, https://doi.org/10.21595/vp.2018.20339

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20339
UR  - https://doi.org/10.21595/vp.2018.20339
TI  - Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount
T2  - Vibroengineering PROCEDIA
AU  - Nguyen, Khac Tuan
AU  - Nguyen, Van Liem
PY  - 2018
DA  - 2018/12/13
PB  - JVE International Ltd.
SP  - 89-95
VL  - 21
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Nguyen_2018,
	doi = {10.21595/vp.2018.20339},
	url = {https://doi.org/10.21595/vp.2018.20339},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	pages = {89--95},
	author = {Khac Tuan Nguyen and Van Liem Nguyen},
	title = {Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]K. T. Nguyen and V. L. Nguyen, “Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount,” Vibroengineering PROCEDIA, vol. 21, pp. 89–95, Dec. 2018, doi: 10.21595/vp.2018.20339.

Copy IEEE

Copied to clipboard!

Nguyen, Khac Tuan, and Van Liem Nguyen. “Enhancing the Ride Comfort of the Off-Road Vibratory Roller Cab by Adding Damper Hydraulic Mount.” Vibroengineering PROCEDIA 21 (December 13, 2018): 89–95. https://doi.org/10.21595/vp.2018.20339.

Copy Chicago

Copied to clipboard!

Enhancing the ride comfort of the off-road vibratory roller cab by adding damper hydraulic mount

Abstract

Highlights

1. Introduction

2. Off-road vehicle model

2.1. Vibratory roller dynamic model

2.2. Cab’s vibration isolation system model

2.3. Dynamic off-road vehicle and deformable soil interaction models

2.3.1. The wheels-deformable soil contact model

2.3.2. The rigid drum and elastic-plastic soil interaction model

3. Results and discussion

3.1. The off-road vehicle travels to the workshop

3.2. The off-road vehicle works in the workshop

4. Conclusions

References

Cited by

About this article

Related Articles