Method of calculating variable section shafts shear deformations

Gordeev, Boris; Okhulkov, Sergei; German, Leonid; Serebryakov, Alexander; Sugakov, Valery

doi:10.21595/vp.2018.20354

Vibroengineering Procedia

Browse Procedia

Published: 13 December 2018

Check for updates

Method of calculating variable section shafts shear deformations

Boris Gordeev¹

Sergei Okhulkov²

Leonid German³

Alexander Serebryakov⁴

Valery Sugakov⁵

^{1, 2, 3, 4}Nizhny Novgorod State Technical University n.a. R.E. Alekseev, Nizhny Novgorod, Russia

⁵Volga State University of Water Transport, Nizhny Novgorod, Russia

Corresponding Authors:

Boris Gordeev, Sergei Okhulkov

Cite the article Download PDF

Downloads 1207

CrossRef Citations 3

Abstract

This article considered method to measure low-frequency angular oscillations of rotors of electric machines and solved the problem of assess shear deformations of rotating shafts in transient conditions. Method of calculating torsional torques is considered by the example of electric generator shaft of diesel generator unit. This method allows taking into account the angular deformations of the rotating shafts, and reducing vibration overloads, and increasing in both resource and reliability.

1. Introduction

Control over rotating electrical machines dynamic state according to the engineering status is carried out by various engineering systems. Vibration diagnostics systems are most important among them [1-6]. The development of such systems is a difficult task, since should be determine the parameters that can estimate the machine state. In addition, it should establish their values, which determine the intervals of a good or fault state of the machine [5, 7, 8]. Finite elements method is used to solve this task [6, 9-12].

2. Requirements to calculate deformations of electrical machines rotating actual shafts

Variable section shafts are often found at the calculations torsional oscillations of the electric machines shafts [13-16]. Often the section of the shaft changes in step from one diameter $D_{1}$ to another $D_{2}$ (Fig. 1). In Fig. 1 shows the shaft of an asynchronous motor 4AK250.

Fig. 1Sketch of motor shaft

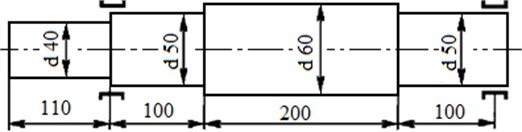
In actual shafts structures at the junctions of shaft areas of different length and diameter there are fillets-corner round-offs at the parts. For such junctions it is necessary to apply the method of determination the equivalent shaft area [9-13].

It is difficult to choose equations for the description of shaft oscillations in the analytical solution of the task, since should be take into account both the general requirements for the initial and boundary conditions and the requirements for intermediate boundary conditions at the shafts junctions [14-17]. These requirements are called join of solution by intermediate end conditions. Using join of solution presents a considerable difficulty at searching for analytical solutions [9, 10, 12].

The use of a difference equation to solve a problem avoids the join of solution, but in this case should be add an additional equation of motion for the junction element of shafts [12]. Torsional oscillations for shafts areas of smaller and bigger diameters can be expressed by differential equation:

1

G \frac{d^{2} φ_{x}}{d x^{2}} = ρ \frac{d^{2} φ_{x}}{d t^{2}},

where $G$ – shear modulus of shaft material, $ρ$ – shaft material density, $φ_{x}$ – actual shaft angle of rotation. Eq. (1) can be written in a difference form:

2

J_{p} G \frac{φ_{x, i + 1} - 2 φ_{x, i} + φ_{x, i - 1}}{h^{2}} = J_{m} \frac{d^{2} φ_{x}}{d t^{2}},

where $J_{m}$ – is an element inertia forces moment (element inertia moment), $J_{p}$ – actual shaft element polar moment, $h$ – mesh step along the actual shaft length.

Dynamic equation for real shaft joint can be expressed:

3

M_{x}^{+} - M_{x}^{-} = J_{m} \frac{d^{2} φ_{x}}{d t^{2}},

where $M_{x}^{+}$ and $M_{x}$ – refer to different shaft areas of different diameters.

The center shaft area of the intermediate element-mesh point is placed at the boundary [12] (Fig. 2(a)).

Fig. 2The center of the: a) shaft area intermediate element-mesh point is placed on the boundary, b) cross-section cut of a shaft in cylindrical coordinate system

The center of the: a) shaft area intermediate element-mesh point is placed on the boundary, b) cross-section cut of a shaft in cylindrical coordinate system

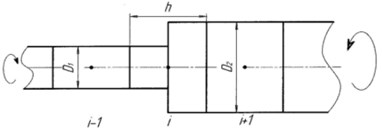
a)

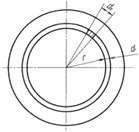
b)

Then instead of Eq. (2) it is necessary to write:

4

J_{2} G_{2} \frac{φ_{x, i + 1, j} - φ_{x, i, j}}{h} - J_{1} G_{1} \frac{φ_{x, i, j} - φ_{x, i - 1, j}}{h} = J_{m c p} \frac{φ_{x, i, j - 1} - 2 φ_{x, i, j} + φ_{x, i, j + 1}}{τ^{2}} .

Shortcut in this case is not possible and it is necessary to calculate both central inertia moments and inertia forces moment – $J_{m c p}$ . For example:

5

J_{1} = \int_{S_{1}}^{} r_{1}^{2} d S, J_{2} = \int_{S_{2}}^{} r_{2}^{2} d S, J_{m c p} = \frac{h}{2} \int_{S_{1}}^{} ρ_{1} r_{1}^{2} d S + \frac{h}{2} \int_{S_{2}}^{} ρ_{2} r_{2}^{2} d S .

In the case of circular section shafts, evaluation of integrals in Eq. (5) is not difficult if cylindrical coordinate system is used (Fig. 2(b)), where $r$ – is shaft radius.

For example, $d S = r d α d r$ and:

6

J_{1} = \int_{0}^{2 π} d α \int_{0}^{R} r^{3} d r = π \frac{R r^{4}}{2} .

The equation $A = (G τ^{2}) / (ρ h^{2})$ is obtained by substituting numerical values into Eq. (4) [12]. Choose an element of constant section with $A =$ 1 as the final element for determining the parameters of the shaft.

3. Determining the reduced shaft length and diameter

Reduced and transmission shafts of electromechanical complexes, travel mechanisms of mobile machines usually have stepped configuration which considerably complicates the task of determining numerical value of torsional rigidity of shaft lines shafts [13-15]. To determine the numerical value of the torsional stiffness of the shaft of a step configuration, it is advisable to substitute the stepped shaft (Fig. 3(a)) with a smooth shaft of equivalent rigidity [13] (Fig. 3(b)).

Now total length of the shaft will be called reduced length $l$ . The diameter shaft is constant through the full length. Now it will be called the reduced diameter $d$ . The shaft length and diameter are the shaft primary geometrical dimensions to determine torsional rigidity numerical value [13, 14, 16].

Fig. 3a) Actual, b) reduced shafts drafts

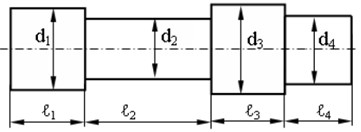
a)

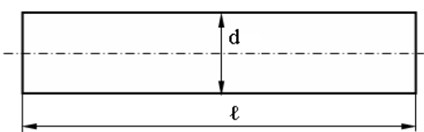
b)

The reduced shaft diameter can be determined by:

7

d = \frac{d_{1} l_{1} + d_{2} l_{2} + d_{3} l_{3} + d_{4} l_{4}}{l_{1} + l_{2} + l_{3} + l_{4}},

where $l$ – reduced shaft length, $d$ – reduced shaft diameter.

The stepped shaft can be considered as discreet bodies connected in series having respective diameters and length. This shaft compliance is determined by summing up shaft areas compliances $e = e_{1} + e_{2} + e_{3} + e_{4}$ .

Shaft torsional rigidity is its inverse compliance value $e = 1 / C$ , it can be:

8

\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} + \frac{1}{C_{4}} .

The shaft torsional rigidity consists of the torsional rigidity of each shaft section:

9

\frac{32 l}{π G d^{4}} = \frac{32 l_{1}}{π G d_{1}^{4}} + \frac{32 l_{2}}{π G d_{2}^{4}} + \frac{32 l_{3}}{π G d_{3}^{4}} + \frac{32 l_{4}}{π G d_{4}^{4}} .

From (9) obtain an equation for the shaft reduced length:

10

\frac{l}{d^{4}} = \frac{l_{1}}{d_{1}^{4}} + \frac{l_{2}}{d_{2}^{4}} + \frac{l_{3}}{d_{3}^{4}} + \frac{l_{4}}{d_{4}^{4}}, l = \frac{l_{1} d^{4}}{d_{1}^{4}} + \frac{l_{2} d^{4}}{d_{2}^{4}} + \frac{l_{3} d^{4}}{d_{3}^{4}} + \frac{l_{4} d^{4}}{d_{4}^{4}} .

Thus, it is possible to calculate the parameters for the dynamic model of the object under study, using such notions as the shaft reduced length and the shaft reduced diameter.

4. Calculating maximum deformations of the electric generator rotor reduced shaft of diesel generator unit

The finite element method [9, 11] is used to estimate the maximum shear deformations of electric generator rotating shaft of unified electric power plants (UEPP) standalone object, caused by torsional torques.

The diesel crankshaft of diesel generator units (DGU) UEPP connected to the rotor of a synchronous electric generator through a plate coupling, absorbing axial, radial and angular displacements with the lowest reaction forces due to its elastic and dissipative properties [10].

The method for estimating rotating shafts maximum shear deformations is described below.

According to the expression $A = (G τ^{2}) / h^{2} =$ 1 time step [9, 11, 12]:

11

τ = h \sqrt{\frac{ρ}{G}} .

Mechanical oscillations propagation speed in solid bodies is determined by:

12

V = \sqrt{\frac{G}{ρ}} = \sqrt{\frac{E}{2 ρ (1 + μ)}},

where $E$ – elastic modulus, $μ$ – Poisson’s ratio.

The shaft SE torsion time ratio [9, 10, 12]:

13

T_{d} = T_{t t} = \frac{L}{V},

where $L$ – measuring reduced shaft length, $V$ – mechanical oscillations propagation speed, $T_{t t}$ – reduced shaft torsion time.

This time does not depend on the torsion velocity of the shaft SE $v_{l}$ , on the steps selected $h$ and $τ$ .

Maximum deformations in all the shaft SE elements turn out to be the same and equal [9, 10, 12]:

14

ε_{m a x} = \frac{v_{l} τ}{h} = v_{l} \sqrt{\frac{2 ρ (1 + μ)}{E}} = \frac{v_{l}}{V} .

For example, the linear velocity of the shaft elements torsion is equal $ν_{l} =$ 162.65·10^-3 m/s for the reduced rotor shaft of DGU electric generator at torsional oscillations frequency $Ω_{t o} =$ 6.28 rad/s and the shaft radius $r =$ 0.0259 m. The electric generator rotor shaft material has the following characteristics: shear modulus $G =$ 8∙10¹⁰ n/m²; $ρ =$ 7,8∙10³ kg/m³, and the mesh step is selected as equal to $h =$ 0,0651 m, then according Eq. (11) the time step becomes equal $τ =$ 20.327·10^-6 s. The electric generator rotor shaft elements are in torsion at the velocity of $ν_{l} =$ 325.3·10^-3 m/s, then from Eq. (14) obtain maximum deformations in all rotor shaft elements equal [9, 10] $ε_{m a x} =$ 50.7875·10^-6.

Thus, maximum deformations in all rotor shaft elements turn out to be small. Therefore, every unit for the rotor shaft elements equals 50,787 microns. Maximum strains in all electric generator shaft elements turn out to be equal [9, 10] $σ = G ε_{m a x} =$ 4063∙10³ N/m².

The maximum reciprocal turn of sections of all elements on the electric generator rotor shaft relative to each other is found by:

15

{∆ φ}_{m a x} = (φ_{x, i + 1} - φ_{x, i}) = \frac{ε_{m a x} h}{r},

Use the following example data: $ε_{m a x} =$ 50.7875·10^-6; $r =$ 0.0259 m; $h =$ 0,0651 m, then the maximum reciprocal turn of sections of all elements on the electric generator rotor shaft relative to each other is a value $Δ φ_{m a x} =$ 1276.55·10^-6rad.

Maximum deformation of the electric generator rotor shaft of the length $L =$ 0.651 m transform to angular units $Δ φ_{m a x} =$ 242.68” = 4.04’ – angular seconds and angular minutes respectively [9, 10].

Maximum time of electric generator rotor shaft torsion of the length $L =$ 0.651 m, at $Ω_{t o} =$ 6.28 rad/s and $T_{o p} =$ 1.0 s will represent a value $T_{d} =$ 203.169·10^-6s.

The admissible torque rating on the electric generator rotor shaft is determined by:

16

M_{s t} = \frac{∆ φ}{L} G \int_{S}^{} R^{2} d S .

Integral in Eq. (16) is a polar moment of inertia of electric generator rotor shaft, of radius $R$ . Electric generator rotor shaft of a uniform section has a polar moment of inertia which is constant along the shaft length and does not depend on the length of its base area $L =$ 0.651 m:

17

J_{p} = \int_{S}^{} R^{2} d S .

Polar moment of inertia is determined expression $J_{p} = (π R^{4}) / 2$ for the electric generator rotor shaft section of radius $R =$ 0.0259 m the [12]. Initial conditions of this task are as follows:

– Shear modulus of the electric generator rotor shaft $G =$ 8∙10¹⁰ N/m².

– Electric generator rotor shaft material density $ρ =$ 7.8∙10³ kg/m³.

– Rigidity.

Then:

{G J}_{p} = \frac{G π R^{4}}{2} = 0.0564 ∙ 10^{6} N m^{2} .

The torque is determined from Eq. (16). Torque is $M_{s t} =$ 110.883 Nm for the electric generator rotor shaft at torsional oscillations frequency $Ω_{t o} =$ 6.28 rad/s.

The irregularity in crankshaft rotational frequency reaches 0.7 % for DGU with an 8-cylinder diesel engine. The engine runs calmer at lower irregularities. Torsional oscillations cyclic frequency is $f =$ 5.0 Hz, or circular frequency is $Ω_{t o} =$ 31.4 rad/s at the irregularity in crankshaft rotational frequency being 0.7 % [10].

The torque equals $M_{s t} =$ 15.968∙10³ Nm at torsional oscillations frequency of DGU crankshaft $f =$ 5.0 Hz from torsional oscillations at end areas (elements) of the crankshaft.

Torque from the crankshaft DGU on the shaft of the electric generator affects the strength of the rotor shaft. This increases the eccentricity of the rotor shaft and vibration, if the crankshaft DGU directly connected to the rotor shaft of the generator [3, 10].

The shaft of the electric generator is connected to the crankshaft of a diesel engine DGU through a plate coupling. In this case, the electric generator rotor shaft operates within the rotational frequency operational range without losing the strength. This ensures smoothness of shaft rotation of the generator and ensures safe operation in the UEPP.

5. Conclusions

The method allows calculating the maximum deformations actual rotating rotor shafts of UEPP generators of standalone objects. The real shafts of actual structures of traction generators rotor have fillets at the junction points of the shaft sections of different diameters. These fillets increase the strength of the shaft and reduce internal stresses. Therefore, the real shafts need to be converted to an equivalent shaft of circular cross section.

References

Thorby D. Structural Dynamics and Vibration in Practice: an Engineering Handbook. Butterworth-Heinemann, Oxford, 2008.

Publisher
Blekhman I. I. Vibrational Mechanics: Nonlinear Dynamic Effects, General Approach, Applications. World Scientific, Singapore, 2000.

Publisher
Thompson D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control. Elsevier, Oxford, 2009.

Publisher
Bialas K. Mechanical and electrical elements in reduction of vibrations. Journal of Vibroengineering, Vol. 14, Issue 1, 2012, p. 123-128.

Search CrossRef
Zhou W., Wei X., Zhai L., Wei X., Wang L. Nonlinear characteristics and stability optimization of rotor-seal-bearing system. Journal of Vibroengineering, Vol. 16, Issue 2, 2014, p. 818-831.

Search CrossRef
Feng N. S., Hahn E. J., Randall R. B. Simulation of Vibration Signals from a Rolling Element Bearing Defect (DSTO-GD-0262). University of New South Wales, Sydney, 2004.

Search CrossRef
Gordeev B. A., Kovrigin D. А., Leontyeva А. V. Rotor synchronization of two motors on an elastic base. Russian Engineering Research, Vol. 31, 2011, p. 923-927.

Publisher
Jauregui J. C. Parameter Identification and Monitoring of Mechanical Systems under Nonlinear Vibration. Elsevier, Cambridge, 2014.

Publisher
Gordeev B. A., Okhulkov S. N., Osmehin А. N., Shohin А. Е. Reducing transient vibrations due to rotating shafts. Russian Engineering Research, Vol. 38, Issue 5, 2018, p. 335-341.

Publisher
Gordeev B. А., Okhulkov S. N., Osmehin А. N., Korendyasev G. K. Assessment of elastic and damping characteristics of rotating shafts magnetorheological box-coupling. Vestnik Mashinostroeniya, Vol. 5, 2018, p. 9-13.

Search CrossRef
Nippes P. I. Early warning of developing problems in rotating machinery as provided by monitoring shaft voltages and grounding currents. IEEE Transactions on Energy Conversion, Vol. 19, Issue 2, 2004, p. 340-345.

Publisher
Matsushita O., Tanaka M., Kanki H., Kobayashi M., Keohg P. Vibrations of Rotating Machinery: Volume 1. Basic Rotordynamics: Introduction to Practical Vibration Analysis. Springer Japan, Tokyo, 2017.

Publisher
Lu C., Wang Y., Ragulskis M., Cheng Y. Fault diagnosis for rotating machinery: A method based on image processing. OLoS ONE, Vol. 11, Issue 10, 2016, p. e0164111.

Publisher
Astashev V. K., Babitsky V. I., Kolovsky M. Z. Dynamics and Control of Machines. Springer, Berlin, 2000.

Publisher
Friswell M. I., Penny J. E. T., Garvey S. D., Lees A. W. Dynamics of Rotating Machines. Cambridge University Press, Cambridge, 2015.

Search CrossRef
Wittenburg J. Dynamics of Multibody Systems. Springer, Berlin, 2008.

Search CrossRef
Goroshko A., Royzman V., Zembytska M. Quality and Reliability of Technical Systems: Theory and Practice. JVE International, 2018.

Search CrossRef

Cited by

Conical Elastic Shell of Hydraulic Vibrational Support

A. I. Ermolaev | B. A. Gordeev | S. N. Okhulkov | A. S. Plekhov | D. Yu. Titov

(2023)

Method for Calculating Deformations and Stresses in an Impact Press Fuse

B. A. Gordeev | V. I. Erofeev | A. I. Ermolaev | S. N. Okhulkov | A. S. Plekhov

(2023)

К РАСЧЁТУ ЖЕСТКОСТИ УПРУГИХ БЛОКОВ МОБИЛЬНЫХ МАШИН МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

(2021)

About this article

Received

06 November 2018

Accepted

15 November 2018

Published

13 December 2018

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2018.20354

Keywords

transient process

torsional oscillations

torsional moment

sensing element

shear deformation

finite elements method

Acknowledgements

The research work has been carried out at the expense of a Russian Science Foundation Grant (Project No. 15-19-10026).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 02

An analytical model for the analysis of vibration and energy flow in a clamped stiffened plate using integral transform technique

Hui Guo, Kai Zhang

Research article

2020 06 30

Exact forced torsional vibration solution of a shaft with multiple discontinuities and arbitrary boundary conditions

Meilong Chen, Shuying Li, Hongliang Li, Siyuan Liu

Research article

2018 12 13

Torque sensors calibration of electromechanical complexes shafts

Sergei Dmitriev, Andrey Daryenkov, Leonid German, Boris Gordeev, Sergei Okhulkov, Alexander Serebryakov

Research article

2015 11 15

Vibration analysis of marine propulsion shafting by the coupled finite element method

Qianwen Huang, Cong Zhang, Yong Jin, Chengqing Yuan, Xinping Yan

B. Gordeev, S. Okhulkov, L. German, A. Serebryakov, and V. Sugakov, “Method of calculating variable section shafts shear deformations,” Vibroengineering PROCEDIA, Vol. 21, pp. 231–236, Dec. 2018, https://doi.org/10.21595/vp.2018.20354

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20354
UR  - https://doi.org/10.21595/vp.2018.20354
TI  - Method of calculating variable section shafts shear deformations
T2  - Vibroengineering PROCEDIA
AU  - Gordeev, Boris
AU  - Okhulkov, Sergei
AU  - German, Leonid
AU  - Serebryakov, Alexander
AU  - Sugakov, Valery
PY  - 2018
DA  - 2018/12/13
PB  - JVE International Ltd.
SP  - 231-236
VL  - 21
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Gordeev_2018,
	doi = {10.21595/vp.2018.20354},
	url = {https://doi.org/10.21595/vp.2018.20354},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	pages = {231--236},
	author = {Boris Gordeev and Sergei Okhulkov and Leonid German and Alexander Serebryakov and Valery Sugakov},
	title = {Method of calculating variable section shafts shear deformations},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]B. Gordeev, S. Okhulkov, L. German, A. Serebryakov, and V. Sugakov, “Method of calculating variable section shafts shear deformations,” Vibroengineering PROCEDIA, vol. 21, pp. 231–236, Dec. 2018, doi: 10.21595/vp.2018.20354.

Copy IEEE

Copied to clipboard!

Gordeev, Boris, Sergei Okhulkov, Leonid German, Alexander Serebryakov, and Valery Sugakov. “Method of Calculating Variable Section Shafts Shear Deformations.” Vibroengineering PROCEDIA 21 (December 13, 2018): 231–36. https://doi.org/10.21595/vp.2018.20354.

Copy Chicago

Copied to clipboard!

Method of calculating variable section shafts shear deformations

Abstract

1. Introduction

2. Requirements to calculate deformations of electrical machines rotating actual shafts

3. Determining the reduced shaft length and diameter

4. Calculating maximum deformations of the electric generator rotor reduced shaft of diesel generator unit

5. Conclusions

References

Cited by

About this article

Related Articles