Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate

Kumar, Anup; Lather, Neeraj; Bhardwaj, Reeta; Mani, Naveen; Sharma, Amit

doi:10.21595/vp.2018.20367

Vibroengineering Procedia

Browse Procedia

Published: 13 December 2018

Check for updates

Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate

Anup Kumar¹

Neeraj Lather²

Reeta Bhardwaj³

Naveen Mani⁴

Amit Sharma⁵

^{1, 2, 3, 5}Amity University Haryana, Gurgaon, India

⁴Sandip University, Nashik, Maharashtra, India

Corresponding Author:

Amit Sharma

Cite the article Download PDF

Downloads 1338

CrossRef Citations 4

Abstract

In this paper, a theoretical analysis is carried out to investigate the effect of linear variation in density and circular variation in Poisson’s ratio on time period of frequency modes of rectangular plate with variable thickness under temperature field. The thickness variation is considered to be circular and temperature variation on the plate is assumed to be bi-linear. Rayleigh Ritz method is used to solve the differential equation. All the results (time period for first two modes of vibration) are presented with the help of tables.

1. Introduction

The study of vibration of non-homogeneous plate is essential in these days because non-homogeneous plate with variable thickness are used in almost all engineering structures such as power plants, wings of an aircrafts, machines, bridges etc. Plates with variable thickness along with non-homogeneity have great impact when compared to homogeneous plate with uniform thickness because of their efficiency and strength. The first few modes of vibration provide us good information about the behavior of systems/structures. Therefore, in order to design perfect structures/systems, it is essential to determine natural frequencies and mode shapes. A significant work has been reported in these directions.

The natural vibration of cantilever plates with variable thickness is analyzed by using mixed boundary grid method (FBGM) [1] and obtained characteristic equation and frequency parameters. A model [2] is presented to analyze the nonlinear vibrations of visco elastic thin rectangular plates by using von Kármán nonlinear strain–displacement relationships and obtained fundamental modes of a simply supported square plate with immovable edges. The nonlinear damping of visco elastic rectangular plate [3] is studied and equation of motion is derived using Lagrange equations. The results are also obtained theoretically as well as experimentally. Vibration analysis of rectangular plates with rectangular cutouts is investigated by using extended Hencky bar-net method (HBM) [4]. Method of reverberation ray matrix (MRRM) and golden section search (GSS) algorithm [5] is applied to obtain the exact solution of rectangular plates with arbitrary boundary conditions. Accurate analytic solutions for natural vibration of thick rectangular plates with a free edge is presented in [6]. Natural vibration of thick rectangular plate [7] without two parallel simply supported edges is studied and new analytic solutions are obtained. The effect of crack defects and temperature on vibration of thin isotropic and orthotropic rectangular plates is studied in [8]. The effect of circular variation in density and exponential variation in Poisson’s ratio on vibrational frequency of parallelogram plate under temperature field is examined in [9]. The effect of two-dimensional thickness and temperature effect on natural vibration of parallelogram plate on clamped edges is studied using Rayleigh Ritz method [10]. Rayleigh Ritz method [11] is used to analyze the natural vibration of isotropic rectangular plate with circular variation in thickness and exponential variation in Poisson’s ratio under temperature field. Free vibration of moderately thick laminated composite rectangular plate with non-uniform boundary conditions is presented by using an improved Fourier series method [12]. Closed-form solution [13] is presented to study the effects of rotary inertia and shear deformation on frequency of natural vibration problems. A mathematical model [14] is presented to analyze the free vibration of rectangular plates with various rectangular cutouts and variable thickness.

In this study, authors show the effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of non homogeneous rectangular plate on clamped edges. Authors also calculate the time period of vibration corresponding to circular variation in thickness and bi linear variation in temperature. The results are presented with the help of tables.

2. Analysis and assumptions

The differential equation for transverse motion of the plate with variable $D_{1}$ and $ν$ i.e., flexural rigidity and Poisson’s ratio is given by:

1

[D_{1} (\frac{\partial^{4} Φ}{\partial ζ^{4}} + 2 \frac{\partial^{4} Φ}{\partial ζ^{2} \partial ψ^{2}} + \frac{\partial^{4} Φ}{\partial ψ^{4}} + \frac{\partial^{2} ν}{\partial ζ^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}}) + 2 \frac{\partial D_{1}}{\partial ζ} (\frac{\partial^{3} Φ}{\partial ζ^{3}} + \frac{\partial^{3} Φ}{\partial ζ \partial ψ^{2}} + \frac{\partial ν}{\partial ζ} \frac{\partial^{2} Φ}{\partial ψ^{2}})

+ \frac{\partial^{2} D_{1}}{\partial ζ^{2}} (\frac{\partial^{2} Φ}{\partial ζ^{2}} + ν \frac{\partial^{2} Φ}{\partial ψ^{2}}) + 2 \frac{\partial D_{1}}{\partial ψ} (\frac{\partial^{3} Φ}{\partial ψ^{3}} + \frac{\partial^{3} Φ}{\partial ψ \partial ζ^{2}} - \frac{\partial ν}{\partial ζ} \frac{\partial^{2} Φ}{\partial ζ \partial ψ})

+ \frac{\partial^{2} D_{1}}{\partial ψ^{2}} (\frac{\partial^{2} Φ}{\partial ψ^{2}} + ν \frac{\partial^{2} Φ}{\partial ζ^{2}}) + 2 (1 - ν) \frac{\partial^{2} D_{1}}{\partial ζ \partial ψ} \frac{\partial^{2} Φ}{\partial ζ \partial ψ}] - ρ l ω^{2} Φ = 0,

where $Φ$ is known as deflection function. The expression for flexural rigidity is $D_{1} = E l^{3} / 12 (1 - ν^{2})$ , where $E$ , $l$ are known as Young’s modulus and thickness of the plate.

In order to avoid complexity, the present study requires some assumptions as:

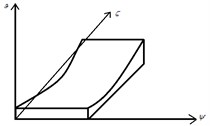
a) Since the plate has variable thickness $l$ , therefore authors considered one dimensional circular variation in thickness as shown in Fig. 1 as:

2

l = l_{0} [1 + β (1 - \sqrt{1 - \frac{ζ^{2}}{a^{2}}})],

where $β$ , (0 ≤ $β$ ≤ 1) is known as tapering parameter. Thickness of plate becomes constant at $ζ =$ 0.

b) For non-homogeneity consideration, authors assumed one dimensional linear variation in density and one dimensional circular variation in Poisson’s ratio as:

3

ρ = ρ_{0} [1 + m_{1} \frac{ζ}{a}],

4

ν = ν_{0} [1 - m_{2} (1 - \sqrt{1 - \frac{ζ^{2}}{a^{2}}})],

where $m_{1}$ , (0 ≤ $m_{1}$ ≤ 1) and $m_{2}$ , (0 ≤ $m_{2}$ < 1) are known as non-homogeneity constants corresponding to density and Poisson’s ratio.

c) The plate is subjected to steady two-dimensional linear temperature distributions as:

5

τ = τ_{0} (1 - \frac{ζ}{a}) (1 - \frac{ψ}{b}),

where $τ$ and $τ_{0}$ denotes the temperature excess above the reference temperature on the plate at any point and at the origin respectively. The temperature dependence modulus of elasticity for engineering structures is given by:

6

E = E_{0} (1 - γ τ),

where $E_{0}$ is the Young’s modulus at mentioned temperature (i.e., $τ =$ 0) and $γ$ is called slope of variation.

Using Eq. (5), Eq. (6) becomes:

7

E = E_{0} [1 - α \{1 - \frac{ζ}{a}\} \{1 - \frac{ψ}{b}\}],

where $α$ , (0 ≤ $α$ < 1) is called temperature gradient, which is the product of temperature at origin and slope of variation i.e., $α = γ τ_{0}$ .

Fig. 1Rectangular plate with one dimensional circular variation

3. Solution for frequency equation and time period

We are using Rayleigh Ritz technique (i.e., maximum strain energy $V_{s}$ must equal to maximum kinetic energy $T_{s}$ ) in order to obtain frequency equation and time period for both modes of vibrations. Therefore, we must have:

8

δ (V_{s} - T_{s}) = 0 .

Here the expression for $V_{s}$ and $T_{s}$ are given by:

9

V_{s} = \frac{1}{2} \int_{0}^{a} ‍ \int_{0}^{b} ‍ D_{1} \times [{(\frac{\partial^{2} Φ}{\partial ζ^{2}})}^{2} + {(\frac{\partial^{2} Φ}{\partial ψ^{2}})}^{2} + 2 ν \frac{\partial^{2} Φ}{\partial ζ^{2}} \frac{\partial^{2} Φ}{\partial ψ^{2}} + 2 (1 - ν) {(\frac{\partial^{2} Φ}{\partial ζ \partial ψ})}^{2}] d ψ d ζ,

10

T_{s} = \frac{1}{2} ω^{2} \int_{0}^{a} \int_{0}^{b} ρ l Φ^{2} d ψ d ζ .

Here, we are computing time period on C-C-C-C condition (i.e., all the four edges are clamped), therefore the boundary conditions are:

11

Φ (ζ, ψ) = \frac{\partial Φ (ζ, ψ)}{\partial ζ} = 0, ζ = 0, a, Φ (ζ, ψ) = \frac{\partial Φ (ζ, ψ)}{\partial ψ} = 0, ψ = 0, b .

Therefore, deflection function (i.e., maximum displacement) which satisfy boundary condition given in Eq. (11) is taken as:

12

Φ (ζ, ψ) = {(\frac{ζ}{a})}^{2} {(\frac{ψ}{b})}^{2} {(1 - \frac{ζ}{a})}^{2} {(1 - \frac{ψ}{b})}^{2} [Ω_{1} + Ω_{2} (\frac{ζ}{a}) (\frac{ψ}{b}) (1 - \frac{ζ}{a}) (1 - \frac{ψ}{b})],

where $Ω_{1}$ and $Ω_{2}$ are arbitrary constants.

Now converting $ζ$ and $ψ$ into non-dimensional variable as:

13

ζ_{1} = \frac{ζ}{a}, ψ_{1} = \frac{ψ}{a} .

Using Eqs. (2)-(4), (7), (9), (10) and (13), Eq. (8) becomes:

14

δ ({V_{s}}^{*} - λ^{2} {T_{s}}^{*}) = 0,

where:

{V_{s}}^{*} = \int_{0}^{1} ‍ \int_{0}^{\frac{b}{a}} ‍ [\{\frac{[1 - α \{1 - ζ_{1}\} \{1 - \frac{a ψ_{1}}{b}\}] {[1 + β (1 - \sqrt{1 - {ζ_{1}}^{2}})]}^{3}}{1 - {ν_{0}}^{2} {[1 - m_{2} (1 - \sqrt{1 - {ζ_{1}}^{2}})]}^{2}}\}

∙ [\begin{array}{l} {(\frac{\partial^{2} Φ}{\partial {ζ_{1}}^{2}})}^{2} + {(\frac{\partial^{2} Φ}{\partial {ψ_{1}}^{2}})}^{2} + 2 ν_{0} [1 - m_{2} (1 - \sqrt{1 - {ζ_{1}}^{2}})] \frac{\partial^{2} Φ}{\partial {ζ_{1}}^{2}} \frac{\partial^{2} Φ}{\partial {ψ_{1}}^{2}} \\ + 2 (1 - ν_{0} [1 - m_{2} (1 - \sqrt{1 - {ζ_{1}}^{2}})]) {(\frac{\partial^{2} Φ}{\partial ζ_{1} \partial ψ_{1}})}^{2} \end{array}]] d ψ_{1} d ζ_{1},

{T_{s}}^{*} = \int_{0}^{1} \int_{0}^{\frac{b}{a}} [1 + m_{1} ζ_{1}] [1 + β (1 - \sqrt{1 - {ζ_{1}}^{2}})] Φ^{2} d ψ_{1} d ζ_{1},

and $λ^{2} = 12 ρ_{0} ω^{2} a^{4} / E_{0} {l_{0}}^{2}$ is known as frequency parameter. Eq. (14) consists of two unknown constants $Ω_{1}$ and $Ω_{2}$ (because of substitution of deflection function $Φ (ζ, ψ))$ . These two unknowns could be calculated as follows:

15

\frac{\partial}{\partial Ω_{n}} ({V_{s}}^{*} - λ^{2} {T_{s}}^{*}) = 0, n = 1,2 .

After simplifying Eq. (15), we get system of homogeneous equations as:

16

\begin{array}{l} c_{11} Ω_{1} + c_{12} Ω_{2} = 0, \\ c_{21} Ω_{2} + c_{22} Ω_{2} = 0 . \end{array}

To obtain non-zero solution (frequency equation), the determinant of coefficient matrix obtain from Eq. (16) must be zero i.e.,

17

|\begin{array}{l} c_{11} & c_{12} \\ c_{21} & c_{22} \end{array}| = 0 .

From Eq. (17), we get a quadratic equation from which we get frequency modes.

The time period of frequency modes is calculated as:

18

K = \frac{2 π}{λ},

where $λ$ is frequeny modes obtained from Eq. (17).

4. Results and discussion

The effect of variation of different plate parameters (non-homogeneity constants $m_{1}$ , $m_{2}$ , thermal gradient $α$ and tapering parameter $β$ ) on time period (in seconds) of vibrations are calculated for fixed value of aspect ratio $a$ / $b =$ 1.5 and presented in tabular form.

Table 1 provides the time period $K$ of vibration corresponding to non-homogeneity $m_{1}$ for two cases i.e., $β = m_{2} = α =$ 0.2 and $β = m_{2} = α =$ 0.6. From Table 1, we can see that time period is increasing with the increasing value of non-homogeneity constant $m_{1}$ for both the cases. While the time period is decreasing with the combined increasing value of taper constant $β$ , non-homogeneity $m_{2}$ and thermal gradient $α$ .

Table 2 accommodates the time period $K$ corresponding to non-homogeneity constant $m_{2}$ for two different cases i.e., $m_{1} = β = α =$ 0.2 and $m_{1} = β = α =$ 0.6. Here, time period is increasing (almost constant) for first case. But for second case, time period is increasing for first mode and time period is decreasing for second mode. The time period is also decreasing when the combined value of thermal gradient $α$ , taper constant $β$ and non-homogeneity constant $m_{1}$ varies from 0.2 to 0.6.

Table 1Non-homogeneity m1 vs. time period K[s] for a/b= 1.5

$m_{1}$	$α = β = m_{2} =$ 0.2		$α = β = m_{2} =$ 0.6
$m_{1}$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
0.0	0.02214	0.08729	0.01848	0.07226
0.2	0.02323	0.09157	0.01941	0.07584
0.4	0.02428	0.09566	0.02030	0.07925
0.6	0.02528	0.09959	0.02115	0.08253
0.8	0.02646	0.10336	0.02197	0.08568
1.0	0.02717	0.10701	0.02276	0.08872

Table 2Non-homogeneity m2 vs. time period K[s] for a/b= 1.5

$m_{2}$	$α = β = m_{1} =$ 0.2		$α = β = m_{1} =$ 0.6
$m_{2}$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
0.0	0.02322	0.09155	0.02113	0.08272
0.2	0.02323	0.09157	0.02114	0.08269
0.4	0.02324	0.09158	0.02114	0.08263
0.6	0.02325	0.09156	0.02115	0.08253
0.8	0.02326	0.09151	0.02115	0.08239

Table 3Taper constant β vs. time period K[s] for a/b= 1.5

$β$	$α = m_{1} = m_{2} =$ 0.4		$α = m_{1} = m_{2} =$ 0.8
$β$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
0.0	0.02837	0.11209	0.03252	0.12384
0.2	0.02492	0.09815	0.02851	0.11193
0.4	0.02211	0.08677	0.02524	0.09864
0.6	0.01979	0.07741	0.02256	0.08776
0.8	0.01786	0.06963	0.02033	0.07877
1.0	0.01623	0.06310	0.01846	0.07125

Table 4Thermal gradient α vs. time period K[s] for a/b= 1.5

$α$	$β = m_{1} = m_{2} =$ 0.4		$β = m_{1} = m_{2} =$ 0.8
$α$	$λ_{1}$	$λ_{2}$	$λ_{1}$	$λ_{2}$
0.0	0.02107	0.08273	0.01848	0.07183
0.2	0.02157	0.08468	0.01890	0.07339
0.4	0.02211	0.08677	0.01934	0.07505
0.6	0.02269	0.08903	0.01982	0.07684
0.8	0.02333	0.09148	0.02033	0.07877

Time period $K$ corresponding to taper constant $β$ is tabulated in Table 3 for the two different cases i.e., $m_{1} = m_{2} = α =$ 0.4 and $m_{1} = m_{2} = α =$ 0.8. Time period is decreasing with the increasing value of taper constant $β$ for both the cases. When we move from first case to second case, the time period is increasing with the increasing value of taper constant $β$ .

Table 4 presents the time period $K$ corresponding to thermal gradient $α$ for two different cases i.e., $m_{1} = m_{2} = β =$ 0.4 and $m_{1} = m_{2} = β =$ 0.8. From Table 4, we conclude that time period is increasing with the increasing value of thermal gradient $α$ for both the cases and decreasing with the combined increasing value of taper constant $β$ and non-homogeneity constants $m_{1}$ , $m_{2}$ .

5. Conclusions

The present study reveals the effect of plate parameters especially density and Poisson’s ratio on time period of vibration of clamped rectangular plate with variable thickness under temperature field. The rate of increment in time period corresponding to non-homogeneity $m_{1}$ (linear variation) is higher than the rate of increment in time period corresponding to non-homogeneity $m_{2}$ (circular variation). Initially, time period (at $m_{2} =$ 0) is high in case of circular variation in non-homogeneity when compared to time period (at $m_{1} =$ 0) in case of linear variation in non-homogeneity. The time period is decreasing corresponding to circular variation in thickness and increasing corresponding to linear temperature variation on plate.

References

Huang M., Xu Y., Cao B. Free vibration analysis of cantilever rectangular plates with variable thickness. Applied Mechanics and Materials, Vol. 130, Issue 134, 2012, p. 2774-2777.

Publisher
Amabili M. Nonlinear vibrations of viscoelastic rectangular plates. Journal of Sound and Vibration, Vol. 362, 2016, p. 142-156.

Publisher
Amabili M. Nonlinear damping in nonlinear vibrations of rectangular plates: derivation from viscoelasticity and experimental validation. Journal of the Mechanics and Physics of Solids, Vol. 118, 2018, p. 275-292.

Publisher
Zhang Y. P., Wang C. M., Pedroso D. M., Zhang H. Extension of Hencky bar-net model for vibration analysis of rectangular plates with rectangular cutouts. Journal of Sound and Vibration, Vol. 432, 2018, p. 65-87.

Publisher
Yuansheng Z., Qingshan W., Dongyan S., Qian L., Zhongyu Z. Exact solutions for the free in-plane vibrations of rectangular plates with arbitrary boundary conditions. International Journal of Mechanical Sciences, Vol. 130, 2017, p. 1-10.

Publisher
Li R., Wang P., Riye X., Xu G. New analytic solutions for free vibration of rectangular thick plates with an edge free. International Journal of Mechanical Sciences, Vol. 131, Issue 132, 2017, p. 179-190.

Publisher
Li R., Wang P., Zheng X., Wang B. New benchmark solutions for free vibration of clamped rectangular thick plates and their variants. Applied Mathematics Letters, Vol. 78, 2018, p. 88-94.

Publisher
Lai S. K., Zhang L. H. Thermal effect on vibration and buckling analysis of thin isotropic/orthotropic rectangular plates with crack defects. Engineering Structures, Vol. 177, 2018, p. 444-458.

Publisher
Sharma A., Sharma A. K., Kumar V. Effect of density and Poisson’s ratio on thermal induced vibration of parallelogram plate. Journal of Vibroengineering, Vol. 20, Issue 3, 2018, p. 1288-1298.

Publisher
SharmaA. Vibrational frequencies of parallelogram plate with circular variations in thickness. Soft Computing: Theories and Application, Advances in Intelligent System and Computing, Vol. 583, 2018, p. 317-326.

Publisher
Sharma A., Mani N., Bhardwaj R. Natural vibration of tapered rectangular plate with exponential variation in non homogeneity. Journal of Vibroengineering, 2018, (in Press).

Publisher
Zhang H., Shi D., Wang Q. An improved Fourier series solution for free vibration analysis of the moderately thick laminated composite rectangular plate with non-uniform boundary conditions. International Journal of Mechanical Sciences, Vol. 121, 2017, p. 1-20.

Publisher
Hwu C., Chang W. C., Gai H. S. Vibration suppression of composite sandwich beams. Journal of Sound and Vibration, Vol. 272, Issues 1-2, 2004, p. 1-20.

Publisher
Shufrin I., Eisenberger M. Semi-analytical modeling of cutouts in rectangular plates with variable thickness – free vibration analysis. Applied Mathematical Modelling, Vol. 40, Issues 15-16, 2016, p. 6983-7000.

Publisher

Cited by

Behavior of frequencies of orthotropic rectangular plate with circular variations in thickness and density

Neeraj Lather | Amit Sharma

(2022)

Time period of transverse vibration of skew plate with parabolic temperature variation

Reeta Bhardwaj | Naveen Mani | Amit Sharma

(2021)

Modelling on vibration of skew plate with thickness and temperature variation

Reeta Bhardwaj | Naveen Mani

(2019)

Natural vibration of skew plate on different set of boundary conditions with temperature gradient

Neeraj Lather | Amit Sharma

(2019)

About this article

Received

02 November 2018

Accepted

14 November 2018

Published

13 December 2018

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2018.20367

Keywords

density

Poisson’s ratio

rectangular plate

time period

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 27

Vibrational analysis of orthotropic rectangular plate having combination of circular thickness and parabolic temperature

Neeraj Lather, Ankit Kumar, Madhu Gupta, Pawan Joshi, Amit Sharma

Research article

2022 04 21

Behavior of frequencies of orthotropic rectangular plate with circular variations in thickness and density

Neeraj Lather, Amit Sharma

Research article

2019 09 30

Analytical solution of a vibrational problem for visco-elastic plate with Kelvin type boundary conditions

Ashish Kumar Sharma, Manoj Kumar Dhiman, Silky Bensal

Research article

2019 03 15

Natural vibration of skew plate on different set of boundary conditions with temperature gradient

Neeraj Lather, Amit Sharma

A. Kumar, N. Lather, R. Bhardwaj, N. Mani, and A. Sharma, “Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate,” Vibroengineering PROCEDIA, Vol. 21, pp. 14–19, Dec. 2018, https://doi.org/10.21595/vp.2018.20367

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20367
UR  - https://doi.org/10.21595/vp.2018.20367
TI  - Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate
T2  - Vibroengineering PROCEDIA
AU  - Sharma, Amit
AU  - Kumar, Anup
AU  - Lather, Neeraj
AU  - Bhardwaj, Reeta
AU  - Mani, Naveen
PY  - 2018
DA  - 2018/12/13
PB  - JVE International Ltd.
SP  - 14-19
VL  - 21
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Sharma_2018,
	doi = {10.21595/vp.2018.20367},
	url = {https://doi.org/10.21595/vp.2018.20367},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	pages = {14--19},
	author = {Amit Sharma and Anup Kumar and Neeraj Lather and Reeta Bhardwaj and Naveen Mani},
	title = {Effect of linear variation in density and circular variation in Poisson's ratio on time period of vibration of rectangular plate},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]A. Sharma, A. Kumar, N. Lather, R. Bhardwaj, and N. Mani, “Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate,” Vibroengineering PROCEDIA, vol. 21, pp. 14–19, Dec. 2018, doi: 10.21595/vp.2018.20367.

Copy IEEE

Copied to clipboard!

Sharma, Amit, Anup Kumar, Neeraj Lather, Reeta Bhardwaj, and Naveen Mani. “Effect of Linear Variation in Density and Circular Variation in Poisson’s Ratio on Time Period of Vibration of Rectangular Plate.” Vibroengineering PROCEDIA 21 (December 13, 2018): 14–19. https://doi.org/10.21595/vp.2018.20367.

Copy Chicago

Copied to clipboard!

Effect of linear variation in density and circular variation in Poisson’s ratio on time period of vibration of rectangular plate

Abstract

1. Introduction

2. Analysis and assumptions

3. Solution for frequency equation and time period

4. Results and discussion

5. Conclusions

References

Cited by

About this article

Related Articles