Research on the influence of ring rib arrangement on vibration and acoustic radiation of cylindrical shell

1. Introduction

The ribbed cylindrical shell structure is widely used in underwater vehicles. The existence of the ring ribs strengthens the strength and hinders the propagation of waves in the structure. It will affect the vibration and radiation characteristics of the structure. The ring ribs of shell are seen as vibration isolation masses [1], and the effect of vibration isolation mass on structural vibration characteristics was widely studied. Yu [2] simplified the ship structure into a double-layer plate structure and studied the vibration and isolation effect of the connecting plate on the double-layer plate structure. According to the effect of the ribbed plate on the structure, Qian [3] studied the propagation characteristics of several arranged vibration isolation masses from the propagation characteristics of single vibration isolation mass. Xia [4] analyzed the vibration attenuation function of L-shaped plate based on wave theory. In the paper [5], the plate structure model of the equal-mass hollow beam and solid beam vibration isolation mass were researched. Ji [6] based on the principle of impedance mismatch, the effect of vibration isolation on the vibration and acoustic radiation in the pedestal was studied. The influence of vibration isolation mass on the vibration acceleration of structural model was studied in the paper [7]. Numerical calculation analysis and experimental research prove that the vibration isolation mass has a good effect on suppressing structural acoustic propagation.

At present, the research on the wave resistance effect of the vibration isolation mass is relatively rare, and the research results mainly come from the study of the plate structure. In this paper, based on the thin shell structure theory and three-dimensional acoustic elastic theory, the vibration and radiated acoustic power of the shell are taken as the target, and the acoustic radiation of the ring rib structure to the cylindrical shell is studied. The influence of different ring rib arrangements on the acoustic radiation was analyzed and discussed. The influence of the ring rib structure on the vibration performance of the cylindrical shell structure and its mechanism are summarized.

2. Theoretical calculation of vibration and acoustic radiation

For the cylindrical shell, the column coordinates $(r,\theta ,z)$ are used for analysis. The coordinate origin is the midpoint of the axis of the cylindrical shell. The corresponding coordinates are $(u,v,w)$. The cylindrical shell has a radius of $a$ and a thickness of $h$. For the thin shell structure $h/a\ll 1$. The modal expansion method can be used to solve the displacement expansion into a series of numbers as follows:

where $m\left(m=\mathrm{0,1},2,\dots \right)$ and $n\left(n=\mathrm{0,1},2,\dots \mathrm{}\right)$ are the Modal order, $k_m$ is the eigenvalue, which can be determined by boundary conditions.

The external force applied to the cylindrical shell structure is $f(\theta ,z)$. Assume that the ring rib has only normal pressure $g(\theta ,z)$ on the shell. The force can be expanded into series forms:

Substitution of Eq. (1) and Eq. (2) into the governing equation gives the vibration equation of the ribbed cylindrical shell, it can be written as follows:

where $Z_{mn}^M$ is the mechanical impedance of the cylindrical shell.

Assume that number of ring ribs in the cylindrical shell is $T$, and the coordinates of the rib in the $z$ direction is $z_j\left(j=\mathrm{1,2},\dots \mathrm{},T\right)$. The total force of the ring rib is expressed as follows:

Substitution of Eq. (5) into Eq. (3), Eq. (3) can be written as:

The modal vibration velocity can be solved by Eq. (6). And so, can the displacement.

The propagation coefficient of a structure can be represented by the vibration between two points. Define the attenuation of the structure acoustic as follows:

In which the vibration displacement of the test point is $u_2$, and the vibration displacement of the reference point is $u_1$.

According to the modal superposition method, the modal response of each order of the structure can be solved, and the radiation wave velocity of each mode is calculated. The acoustic pressure wave acoustic pressure expression in the frequency domain is as follows [8]:

where ${\rho }_0$ is Fluid density, ${\varphi }_r$ is the $r$th mode radiated wave velocity potential, $q_r$ is the $r$th coordinate component.

The radiated acoustic power of the shell is:

3. The influence of ring rib on vibration and acoustic radiation of cylindrical shell

This paper focuses on the normal vibration of the structure, taking cylindrical shells with different ribbed forms as analytical models. The cylindrical shell is simple support at both ends. The thickness is 0.01 m. The radius is 1 m. The length is 4 m. The thickness of rib is 0.01 m and the height is 0.1 m. The material of the structure is steel, and so are the ring ribs. A unit force is acted near the left end of the bottom of the structure, observing the vibration response and its attenuation at the position of the excitation position to the symmetrical end. The schematic diagram of the model is shown in Fig. 1.

Fig. 1Schematic diagram of ribbed cylindrical shell structure

3.1. The influence of ring rib on vibration of cylindrical shell

In order to research the influence of ring ribs on the vibration of cylindrical shell structure, a non-ribbed cylindrical shell and a single ribbed cylindrical shell were established. Fig. 2 shows the result of the vibration attenuation from the test point to the excitation point.

It can be seen that the vibration attenuation before and after the ribbed is similar at low frequency, and the change is obvious after 200 Hz. When it is not ribbed, the attenuation effect is worse than that of the ribbed cylindrical shell, the vibration attenuation has a negative value around 90 Hz, and the cylindrical shell structure before ribbed has the maximum attenuation at the frequency 230 Hz. After ribbed, the frequency of the maximum attenuation is around 320 Hz. The physical mechanism is that the structure vibration wavelength is longer at low frequency, and the ring rib has less suppression effect on the structure wave; as the frequency increases, the structural vibration wavelength becomes shorter, and the ring rib has a greater suppression effect on the structure wave, and the vibration isolation, the effect is increased.

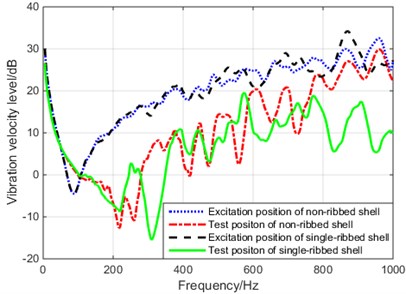
The vibration velocity level of the structural excitation position and the test position (reference velocity is 10^-6 m/s) was analyzed as shown in Fig. 3. It can be seen that the vibration velocity of the excitation position does not change much before and after ribbed, especially when the frequency is below 400 Hz. The vibration velocity of the test position is only changed less than 200 Hz before and after ribbed. The change above 200 Hz is very obvious, which is related to vibration attenuation. The change of the quantity is consistent; the anti-resonance peak appears at the excitation position at 90 Hz, and the anti-resonance peak at the test position appears near 210 Hz. Due to the change of the anti-resonance peak, the extreme frequency of the structural vibration attenuated also changes.

Fig. 2Vibration attenuation of non-ribbed cylindrical shell and single-ribbed cylindrical shell

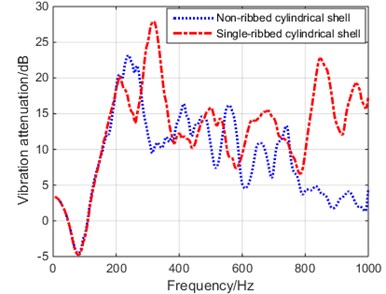
Fig. 3Vibration velocity level of non-ribbed cylindrical shell and single- ribbed cylindrical shell

4. The influence of the distribution of ring rib on the acoustic radiation of cylindrical shell

For the cylindrical shell model researched above, the three-dimensional hydroelastic theory was used to calculate the radiated acoustic power. The calculation result was shown in Fig. 6. It can be seen that at the low frequency, the radiated acoustic power of the non-ribbed cylindrical shell and the single-ribbed cylindrical shell all show peaks, while the multi- ribbed structure does not show peaks at the low frequency, and the third appear obvious near 150 Hz. At the middle frequency, the radiated acoustic power of the non-ribbed structure and the single ribbed structure is not much different, and the radiated acoustic power of the multi- ribbed structure is slightly reduced. At the high frequency band, the radiated acoustic power of the multi-ribbed structure is significantly higher than that of non-ribbed structure and single ribbed structure. The physical mechanism is as follows: the cylindrical shell structure shell is thin, and it is easy to generate low-frequency breathing mode. When the ring rib is applied in the structure, the respiratory mode frequency of the structure becomes larger, but the bending rigidity of the ring rib is not significant. When the number of inner ring ribs in the structure increases to a certain number, the respiratory modal frequency will be higher than the first-order bending mode frequency of the structure. The non-ribbed structure and the single- ribbed structure in the text have obvious peaks at low frequencies, which is due to the low structure. The peak breathing mode is caused, and the peaks appearing at the same time at 150 Hz are caused by the first-order bending mode of the cylindrical shell. Since then, due to the suppression of the ribs, the radiated acoustic power of the multi-ribbed structure in the middle frequency band is slightly lower than that of the non-ribbed structure, but at the same time, due to the strengthening effect of the ribs, the low-order mode of the structure is high-frequency, so that the multi-ribbed structure the radiated acoustic power at high frequencies is higher than that of without ribs.

Fig. 4Vibration attenuation of single-ribbed cylindrical shell and multi-ribbed cylindrical shell

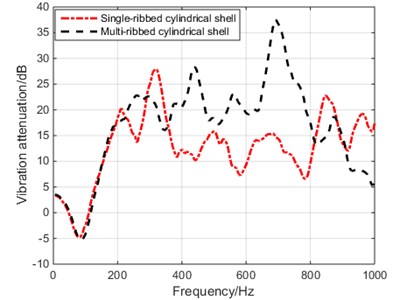
Fig. 5Vibration velocity level of single-ribbed cylindrical shell and multi-ribbed cylindrical shell

Fig. 6Radiated acoustic power level of cylindrical shell structure with different ribbed forms

5. Conclusions

In this paper, the vibration variation of the cylindrical shell before and after the ring rib and after adding multiple ring ribs are compared and analyzed. Summarizing its general laws, and discussing the effects of different ribbed forms on structural acoustic radiation, the main conclusions are as follows.

The influence of the arrangement of the ring ribs on the vibration of the cylindrical shell is mainly reflected at the medium and high frequency and has little effect on the low frequency. The ring ribs changes the maximum attenuation frequency of the cylindrical shell, and as the number of ring ribs increases, the maximum attenuation frequency also increases. The vibration attenuation of the structure under multi-ribbed is higher at the middle frequency than the single ribbed shell, and the high frequency is lower. The multi-ring rib structure can reduce the medium-low frequency radiated acoustic power of the structure, but it will affect the high-frequency acoustic radiation characteristics of the structure.