The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached

Zhang, Junjie

doi:10.21595/vp.2018.20093

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2018

Check for updates

The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached

Junjie Zhang¹

¹China Ship Development and Design Center, National Key Laboratory on Ship Vibration and Noise, Wuhan, China

Cite the article Download PDF

Downloads 1410

CrossRef Citations 1

Abstract

The vibration control of cylindrical shell with dynamic vibration absorber (DVA) periodically and non-periodically attached is investigated. The coupled equations of cylindrical shell-DVA are established at first, and then the method to solve the equations is deduced. Parameters and coordinates of DVA are optimized to get the minimum mean square velocity (MSV) of cylindrical shell. Research results show that: (1) for DVA attached to cylindrical shell periodically, the number of DVA should be moderate, cannot be more or less; (2) the vibration reduction with DVA non-periodical arrangement attached to shell is better than that of periodical arrangement

1. Introduction

DVA is applied to control the structure vibration and noise usually. In order to improve the control effect, parameters of DVA are optimized. The optimization of DVA in single degree-of-freedom (SDOF) and multi-degree-of-freedom (MDOF) system is classical optimization problems and has been already solved for a long time. For the continuous systems, the optimization of DVA published is focused on beam and plate, rarely about shell.

For a continuous structure such as a beam with DVA attached, vibration may be eliminated at the attachment point, while at other parts the vibration may be amplified. So, the vibration of whole structure may be more suitable to evaluate the vibration control effect of DVA. Lu [1] optimized the position and parameters of DVA to minimize the vibration of a simply supported beam. Nagaya [2] presented a method using neural network procedure to decrease vibration and noise from a plate. Wan [3] applied the admittance theory to control the vibration of a simply supported plate with DVA attached. Cheung [4] presented an optimization method to suppress vibration in plate, and got some interesting results. Fuller [5, 6] presented a technique to minimize the radiation sound of cylindrical shell. Achenbach [7] used the Lagrange equations and Donnell-Mushtari shell theory to suppress the vibration of cylindrical shell with DVA attached. It is showed that the control effect of DVA to radiation sound is good.

In the present paper, DVAs are applied to suppress vibration of cylindrical. DVAs are arranged in two categories: periodical and non- periodical arrangement. The PatternSearch optimization algorithm is used to minimize the MSV of shell. The results show that: (1) the number of DVA should be moderate, cannot be more or less for periodic DVAs arrangement; (2) the effect of vibration control with DVA non- periodical arrangement is better than the DVA with periodical arrangement.

2. Theory

2.1. Vibration of cylindrical shell

Cylindrical shell with DVAs attached is showed in Fig. 1, the radius of shell is $R$ , length is $L$ . The axial, circumferential and radial coordinate are denoted by $x$ , $θ$ and $r$ , respectively. $w$ , $v$ and $u$ are the displacements in the $x$ , $θ$ and $r$ directions.

Fig. 1Cylindrical shell attached with DVA

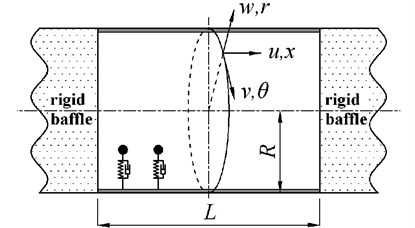
The vibration of cylindrical shell is described by Flügge equations. If the force is only excited in the radial direction, radial displacement of shell can be expressed according to the displacement impedance as:

1

Z_{m n} W_{m n}^{α} = F_{m n}^{α} + T_{m n}^{α},

where, $W_{m n}^{α}$ is radial displacement amplitude, $Z_{m n}$ is displacement impedance, $F_{m n}^{α}$ is external force, $T_{m n}^{α}$ is force exerted by DVA.

The radial displacement in time domain is expressed as:

2

w = \sum_{α = 0}^{1} \sum_{m = 1}^{\infty} \sum_{n = 0}^{\infty} W_{m n}^{α} s i n (n θ + \frac{α π}{2}) s i n (\frac{m π}{L} x) .

2.2. Force exerted to shell by DVA

The sketch of DVA-shell is plotted in Fig. 2, the coupled equation is given by:

3

m {\ddot{z}}_{0} + c ({\dot{z}}_{0} - {\dot{w}}_{0}) + K (z_{0} - w_{0}) = 0,

where, $m$ , $c$ and $K$ is mass, damping coefficient and spring stiffness. $w_{0}$ is displacement of attachment point, $z_{0}$ is displacement of mass.

Fig. 2The sketch of DVA-shell

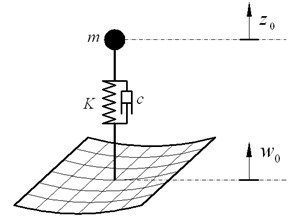
The force of DVA is:

4

T (θ_{0}, x) = c ({\dot{z}}_{0} - {\dot{w}}_{0}) + K (z_{0} - w_{0}) = T_{D V A} w_{0},

where, $T_{D V A} = \frac{m ω^{2} (i c ω + K)}{K - m ω^{2} + i c ω}$ .

The orthogonality of trigonometric function is applied to Eq. (4), the force exerted to shell by the number $j$ DVA is:

5

T_{m n_{j}}^{α} = T_{j} t_{m n_{j}}^{α} w_{j},

where, $T_{j} = \frac{m_{j} ω^{2} (i c_{j} ω + K_{j})}{K_{j} - m_{j} ω^{2} + i c_{j} ω}$ , $w_{j}$ is attachment point of the number $j$ DVA and shell:

t_{m n_{j}}^{α} = \frac{ε_{n}}{π L R} s i n (n θ_{j} + \frac{α π}{2}) s i n (k_{m} x_{j}), ε_{n} = \{\begin{array}{l} 1, n = 0, \\ 2, n \geq 1 . \end{array}

2.3. The external force

Using the orthogonality of trigonometric function, the external force of the number $i$ is:

6

F_{m n_i}^{α} = F_{i} f_{m n_i}^{α},

where, $f_{m n_{i}}^{α} = \frac{ε_{n}}{π L R} s i n (n θ_{i} + \frac{α π}{2}) s i n (k_{m} x_{i})$ .

2.4. Solution and optimization

2.4.1. Vibration solution

Substituting Eq. (5), (6) into Eq. (1), after rearranged, the expression can be written as:

7

W_{m n}^{α} = \frac{F_{m n}^{α} + T_{m n}^{α}}{Z_{m n} + L_{m n}} = \frac{\sum_{i} F_{i} f_{m n_{i}}^{α} + \sum_{j} T_{j} t_{m n_{j}}^{α} w_{j}}{Z_{m n}} .

Substituting Eq. (7) into Eq. (2), the displacement of shell is expressed as:

8

w (x, θ) = \sum_{α = 0}^{1} \sum_{m = 1}^{\infty} \sum_{n = 0}^{\infty} \frac{\sum_{i} F_{0_{i}} f_{m n_{i}}^{α} + \sum_{j} w_{j} T_{D V A_{j}} t_{m n_{D V} A_{j}}^{α}}{Z_{m n}} s i n (n θ + \frac{α π}{2}) s i n (k_{m} x) .

Set the ( $x$ , $θ$ ) to ( $x_{j}$ , $θ_{j}$ ) (attachment point of $j$ DVA and shell) each time, and solve the linear equations, the displacement $w_{j}$ is gotten. Then substituting $w_{j}$ into Eq. (7), the $W_{m n}^{α}$ is solved.

The MSV is used to describe the vibration of the whole shell:

9

\begin{array}{l} ⟨\dot{w} {\dot{w}}^{*}⟩ = \frac{1}{2 S} \int_{S} (\dot{w} {\dot{w}}^{*}) d S = \frac{1}{4} \sum_{α = 0}^{1} \sum_{m = 1}^{\infty} \sum_{n = 0}^{\infty} \frac{1}{ε_{n}} {\dot{W}}_{m n}^{α} {\dot{W}}_{m n}^{α *} \end{array} .

2.4.2. Optimization method

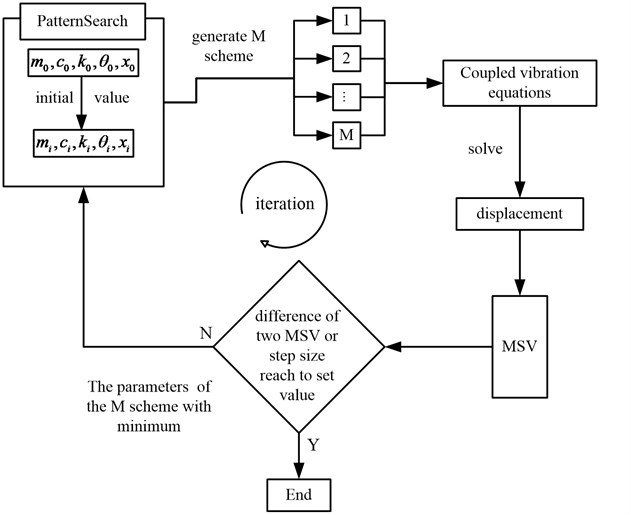
The expression of MSV is complex in Eq. (9), so the minimum of MSV may be gained only by numerical optimization algorithm. The PatternSearch numerical optimization algorithm is recommended, and it can be called in Matlab.

The flow diagram of optimization is showed in Fig. 3. The optimization algorithm is iterated until the difference between the two iteration MSV or step size reach to set value.

Fig. 3The flow diagram of numerical optimization algorithm

3. Numerical calculations and discussions

Two unit forces are acted at position of ( $0$ , $L / 2$ ) and ( $π / 4$ , $3 L / 4$ ). Total mass of DVA is 10 kg, damping coefficient is $c =$ 200 N/m, frequency range is 50 Hz to 200 Hz, and frequency interval is 1 Hz. The participation modal of cylindrical shell $m =$ 25, $n =$ 25 (converged).

3.1. Cylindrical shell without DVA attached

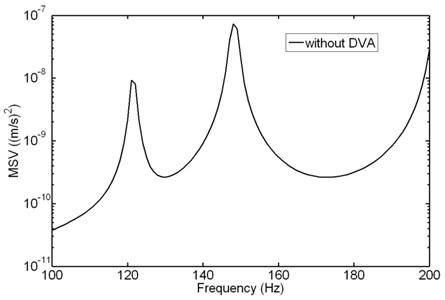
Fig. 4 depicts the MSV of shell without DVA attached. There are two peaks in the curve, and the frequency is 121 Hz and 148 Hz respectively. The total MSV at frequency band [50-200 Hz] is 3.54e-07 (m/s)². In the following discussion, the value 3.54e-07 (m/s)² is used as the reference value to analyze the vibration reduction of cylindrical shell with DVA attached.

Fig. 4MSV of shell without DVA attached

3.2. Cylindrical shell with DVA periodical arrangement

The DVAs are arranged 6×6 on cylindrical shell periodically according to phononic crystals. The axial coordinates are $x =$ 0.15 m, 0.45 m, 0.75 m, 1.05 m, 1.35 m, 1.65 m; circumferential coordinates are $θ =$ 0, $π / 3$ , $2 π / 3$ , $π$ , $4 π / 3$ , $5 π / 3$ . Mass of each DVA is 10/36 = 0.278 kg.

3.2.1. MSV with different spring stiffness

The total MSV with different spring stiffness of DVA is analyzed, showed in Table1. The spring stiffness is equivalent to characteristic frequency by the formula $\sqrt{k / m} / 2 π$ . It is showed that the optimization stiffness is 2.37e5 N/m (characteristic frequency 147 Hz), and the total MSV is 1.56e-7 (m/s)². In the Table 1, the vibration reduction is about 2.4 dB-3.6 dB, so when the coordinates of DVAs and total mass are fixed, if only the spring stiffness is optimized, one cannot get the better vibration control effect.

Table 1MSV with different spring stiffness

Frequency (Hz)	50	100	121	148	200	147 (optimum)
MSV (m/s)²	2.06e-7	1.77e-7	1.64e-7	1.57e-7	1.95e-7	1.56e-7
Vibration reduction(dB)	2.4	3.0	3.3	3.5	2.6	3.6

3.2.2. MSV with different total mass

Keep the stiffness 2.37e5 N/m constant, and change the total mass of DVA to analyze the influence of the total mass to total MSV, expressed in Table 2. It is showed that the total MSV decreases as the total mass increase, but when the total mass excesses 15 kg, the total MSV is no obvious decrease. So, it is not wise to get more vibration reduction through sustaining to increase the total mass.

Table 2MSV with different total mass

Total mass (kg)	5	10	15	20	25	30
MSV (m/s)²	2.49e-7	1.56e-7	1.26e-7	1.14e-7	1.09e-7	1.07e-7
Vibration reduction(dB)	1.5	3.6	4.5	4.9	5.1	5.2

3.2.3. MSV with spring stiffness and coordinates optimized for different DVAs arrangement

Keep the total mass 10 kg constant. The periodic arrangement schemes of DVAs are 6×6, 5×5, 4×4, 3×3, 2×2, and the results of both stiffness and coordinates optimized are showed in the Table 3. Total MSV decreases at first, and then increases as the number of DVA decreases. So, for periodic DVA arrangement, the number of DVA should be moderate, cannot be more or less.

Table 3Optimize spring stiffness and coordinates for different DVAs arrangement

Scheme number	DVAs arrangement	Total MSV(m/s)²	Vibration reduction(dB)
1	6×6	1.04e-7	5.3
2	5×5	8.14e-8	6.4
3	4×4	6.04e-8	7.7
4	3×3	7.16e-8	6.9
5	2×2	8.99e-8	6.0

For the 6×6 DVAs arrangement, if only the spring stiffness is optimized, the total MSV is 1.56e-7 (m/s)² (showed in Table 1); if spring stiffness and coordinates both are optimized, the total MSV is 1.04e-7 (m/s)² (showed in Table 3). So, through multiple parameters optimization, the total MSV decreases more about 33.6 %. Compared to Table 3, it can be gotten less MSV through multiple parameters optimization relative to increase total mass.

3.3. Cylindrical shell with DVA non-periodical arrangement

For the DVA non- periodical arrangement, mass of each DVA is equal and equal to 10 kg/number of DVA. Stiffness, circumferential and radial coordinates of each DVA are optimized. The total MSV with different number of DVA is showed in Table 4. With the increase of number of DVA, the total MSV of shell is decreased effectively, but when the number of DVA is greater than 4, the MSV decrease is no obvious.

Table 4The total MSV with different Scheme number

Scheme number	Number of DVA	Total MSV (m/s)²	Vibration reduction (dB)
Scheme 1	1	1.47e-07	3.8
Scheme 2	2	6.56e-08	7.3
Scheme 2	3	4.01e-08	9.5
Scheme 4	4	2.82e-08	11.0
Scheme 5	5	2.34e-08	11.8
Scheme 6	7	2.20e-08	12.1

Comparing the Table 3 and Table 4, it is showed that when the number of DVA is equal or greater than 3, the vibration reduction with DVA non- periodical arrangement is better than that of periodical arrangement.

4. Conclusions

1) The coupled equations of DVA-shell are established, and the optimization method of vibration reduction is recommended.

2) For DVAs attached to cylindrical shell periodically according to photonic crystals, the number of DVAs should be moderate, cannot be more or less.

3) The vibration reduction with DVA non-periodical arrangement attached to shell is better than that of periodical arrangement.

References

Lu Yihua Research on Undamped Vibration Absorber Attached to the Continuous Systems. Nanjing University of Aeronautics and Astronautics, Nanjing, 2005.

Search CrossRef
Nagya K., Li. L. Control of sound noise radiated from a plate using dynamic absorber under the optimization by neural network. Journal of Sound and Vibration, Vol. 208, Issue 2, 1997, p. 289-298.

Publisher
Wan Minhong The Study on Vibration Control of Thin Plate. Northwestern Polytechnical University, Xi’an, 2007.

Search CrossRef
Cheung Y. L., Wong W. O. H∞ and H2 optimizations of a dynamic vibration absorber for suppressing vibrations in plates. Journal of Sound and Vibration, Vol. 320, Issues 1-2, 2009, p. 29-42.

Publisher
Fuller C. R., Silcox R. J. Active structural acoustic control. Journal of Acoustical Society of America, Vol. 91, 1992, p. 519.

Publisher
Fuller C. R., Maillard J. P., Mercadal M., Von Flotow A. H. Control of aircraft interior noise using globally detuned vibration absorbers. Proceedings of 1st CEAS/AIAA Aeroacoustics Conference, Munich, 1995, p. 615-624.

Search CrossRef
Achenhach J. D. Effect of a vibrating substructure on acoustic radiation from a cylindrical shell. Transactions of the ASME, Vol. 114, Issue 3, 1992, p. 312-318.

Publisher

Cited by

Design of cylindrical metashells with piezoelectric materials and digital circuits for multi-modal vibration control

Danjie Yin | Kaijun Yi | Zhiyuan Liu | Anfu Zhang | Rui Zhu

(2022)

About this article

Received

20 July 2018

Accepted

05 August 2018

Published

19 October 2018

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2018.20093

Keywords

cylindrical shell

dynamic vibration absorber (DVA)

mean square velocity (MSV)

optimization algorithm

vibration reduction

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 06 23

Uncertainty analysis for cylindrical structure vibration according to generalized polynomial chaos method

Chen Luyun, Hong Yi

Research article

2022 12 12

A position optimization strategy of the dynamic vibration absorber for the noise control of the power equipment

Mingxin Geng, Jiangang Ma, Yan Jing, Yalin Zhao, Lv Wang

Research article

2022 04 21

Optimal analysis on low frequency line spectrum sound control of power equipment using dynamic vibration absorber

Jiangang Ma, Jian Wu, Mingxin Geng, Bo Ma, Chen Shen

Research article

2019 02 15

Research of multi-point adaptive control strategy based on electromagnetic active vibration absorber

Weipeng Gao, Guo He, Shuyong Liu

J. Zhang, “The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached,” Vibroengineering PROCEDIA, Vol. 20, pp. 5–10, Oct. 2018, https://doi.org/10.21595/vp.2018.20093

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20093
UR  - https://doi.org/10.21595/vp.2018.20093
TI  - The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached
T2  - Vibroengineering PROCEDIA
AU  - Zhang, Junjie
PY  - 2018
DA  - 2018/10/19
PB  - JVE International Ltd.
SP  - 5-10
VL  - 20
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Zhang_2018,
	doi = {10.21595/vp.2018.20093},
	url = {https://doi.org/10.21595/vp.2018.20093},
	year = 2018,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	pages = {5--10},
	author = {Junjie Zhang},
	title = {The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]J. Zhang, “The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached,” Vibroengineering PROCEDIA, vol. 20, pp. 5–10, Oct. 2018, doi: 10.21595/vp.2018.20093.

Copy IEEE

Copied to clipboard!

Zhang, Junjie. “The Optimization Analysis on the Vibration Control of Cylindrical Shell with Dynamic Vibration Absorber Attached.” Vibroengineering PROCEDIA 20 (October 19, 2018): 5–10. https://doi.org/10.21595/vp.2018.20093.

Copy Chicago

Copied to clipboard!

The optimization analysis on the vibration control of cylindrical shell with dynamic vibration absorber attached

Abstract

1. Introduction

2. Theory

2.1. Vibration of cylindrical shell

2.2. Force exerted to shell by DVA

2.3. The external force

2.4. Solution and optimization

2.4.1. Vibration solution

2.4.2. Optimization method

3. Numerical calculations and discussions

3.1. Cylindrical shell without DVA attached

3.2. Cylindrical shell with DVA periodical arrangement

3.2.1. MSV with different spring stiffness

3.2.2. MSV with different total mass

3.2.3. MSV with spring stiffness and coordinates optimized for different DVAs arrangement

3.3. Cylindrical shell with DVA non-periodical arrangement

4. Conclusions

References

Cited by

About this article

Related Articles