Effect of reducing the vibration of a frame-spacing arrangement

2.1. Vibration localization of aperiodic structures

According to the vibration characteristics of simple structures, such as one-dimensional aperiodic mass-spring chain models, and one-dimensional aperiodic bending beams, the generation of vibration localization mainly meets the following two conditions [25]:

1) The parameter arrangement of the substructure is random.

2) The larger the number of the substructure, the quicker the amplitude of the structural wave decays with increasing propagating distance.

When the sum of frames is enough, and the frame spacing is random, then the vibration localization may be found for finite-length cylindrical shell.

The detailed positions of the frames along the shell are distributed randomly within a small region about the nominal periodic location; i.e., the probability density that the position of a particular frame near $x=nd$ has position $x$ is:

where $d$ is the mean spacing of the frames along the shell, $n$ is the number of a particular frame, $\mathrm{\Delta }x$ is the maximum deviation of the position of a frame from its nominal periodic location. $\mathrm{\Delta }x$ reflects the extent to which the detailed positions of the frames along the shell are distributed randomly. For finite-length cylindrical shell, in order to obtain obvious vibration localization effect, the $\mathrm{\Delta }x$ should be increased as much as possible under the condition of guaranteeing the random distribution of frames spacing.

2.2. Calculation method of vibration localization

The mean square normal velocity of the surface is adopted to show the vibration characteristics of the framed cylindrical shell. For the arbitrary surface $S$, the normal velocity distribution of the shell is $v(x,y,z,t)$, and the mean square normal velocity $〈{\stackrel{-}{v}}^2〉$ of the shell can be obtained:

where $t$ is time, $T$ is integration time length, $S_{\partial }$ is area of $S$.

At the typical frequency of the excited force, the vibration response of the cylindrical shell was calculated by FEM. Then, the mean square normal velocity was obtained by using the vibration response $v(x,y,z,t)$ as the input [26]:

where $N$ is the sum of the finite elements of the shell, $\left|v_i\right|$ is the amplitude of the normal velocity at the centroid of the $i$’th element, $S_i$ the area of the $i$’th element. By taking the logarithm of $〈{\stackrel{-}{v}}^2〉$, the $〈{\stackrel{-}{v}}^2〉$ level $L_{{\stackrel{-}{v}}^2}$ is obtained:

where $v_{ref}=$ 5.0×10^-5 mm/s is the reference velocity.

By comparing the $〈{\stackrel{-}{v}}^2〉$ of the cylindrical shells with frame periodicity and with frame aperiodicity, the reducing vibration effect of a frame-spacing arrangement is explored.

3.1. Structural design of framed cylindrical shell

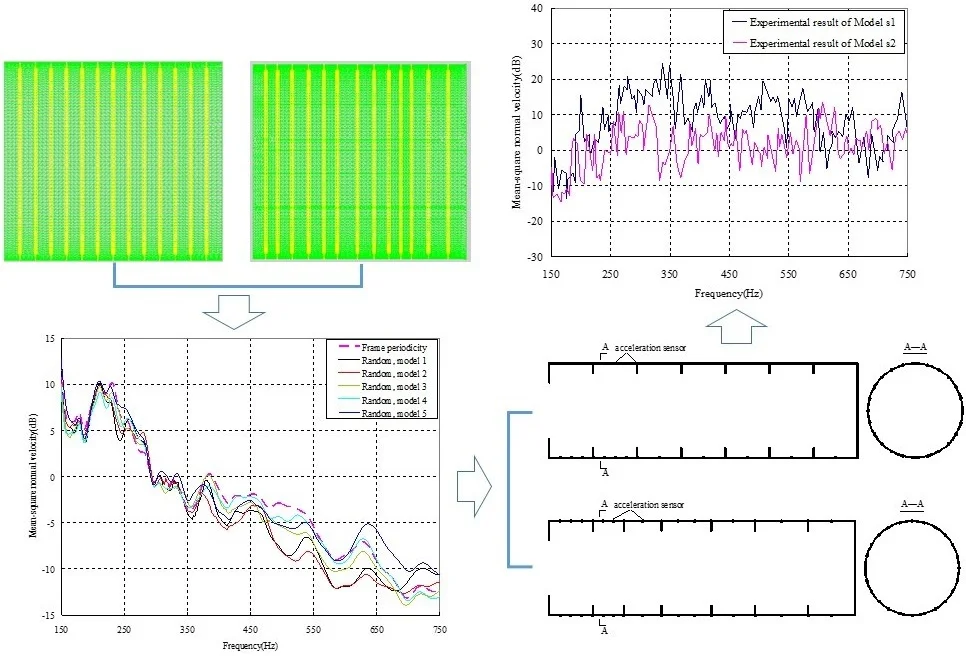
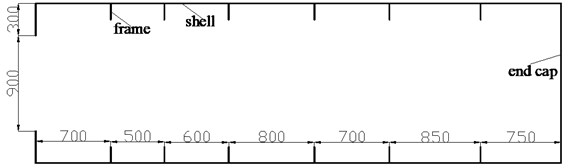
For the studied cylindrical shell with frame periodicity, the frame spacing was 0.6 m, the shell thickness 0.028 m, and the length 8.4 m, and the bulkhead on the two sides was kept invariant; the structural form is shown in Fig. 1.

On the base of the above cylindrical shell with frame periodicity, design the random arrangement of frame spacing. The probability density of the position of a particular frame $x$ satisfies Eq. (1), in which $d=$ 0.6 m, $\mathrm{\Delta }x$ equal to 3.5 % of the frame spacing of the cylindrical shell with frame periodicity, $\mathrm{\Delta }x/d=$ 0.035. There were 13 frames for each cylindrical shell; $n=$ 13, that is to say, 14 frame spacings were generated by the random method, with each measuring 0.4–0.8 m in length. Fifty groups of frame spacings were generated; in other words, 50 framed cylindrical shell models were made, named models 1-50, as shown in Table A1 (in Appendix). Obviously, the arrangement of frame spacing is aperiodic, e.g. the sketches of the frame-spacing arrangement of model 1 is shown in Fig. 2.

Fig. 1Structure design of cylindrical shell with frame periodicity

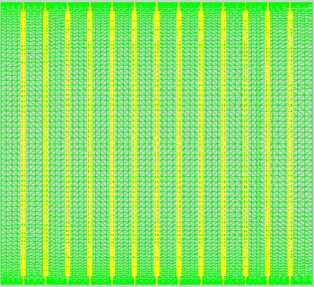
Fig. 2Frame-spacing arrangement of model 1

3.2. Vibration response of framed cylindrical shell in air

The vibration responses of the cylindrical shell with frame periodicity and frame aperiodicity were separately calculated by FEM in air, and MSC.Patran was used to build the models of the framed cylindrical shell, therefore the accuracy of the calculation was guaranteed.

There are two calculation cases: one is the application of axial exciting force acting on the base of the floating raft, and the other is the application of vertical exciting force acting on the base of the floating raft. The frequency band of the exciting force is 20-1000 Hz, and the calculation result of the mean square normal velocity which was obtained by Eq. (3) is compared and analyzed.

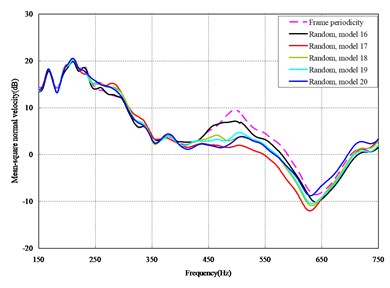
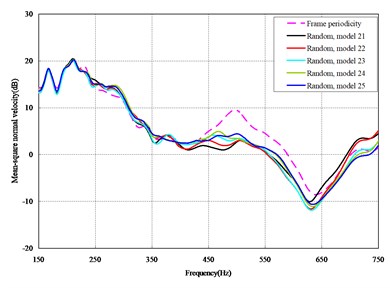
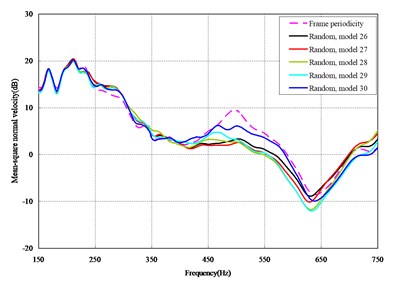
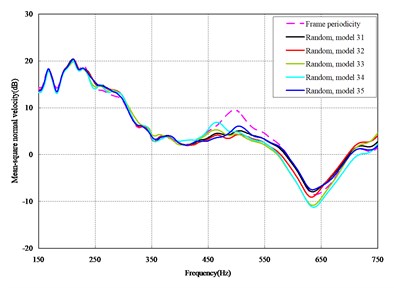
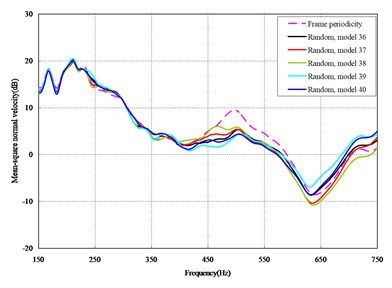
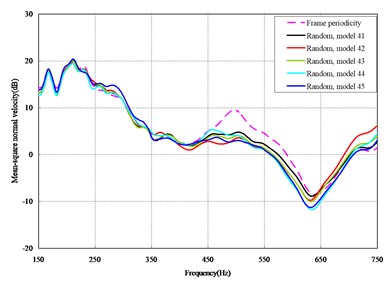
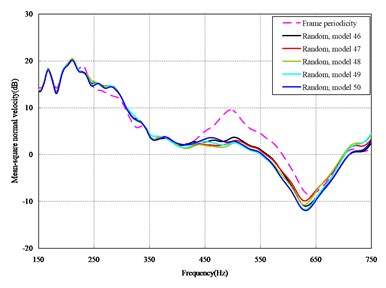
Fig. 3Comparison among 50 models under axial loads

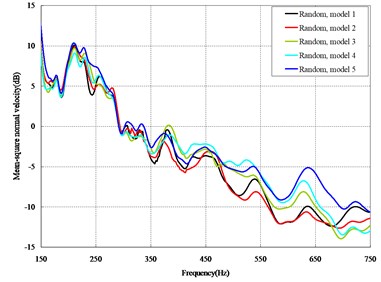
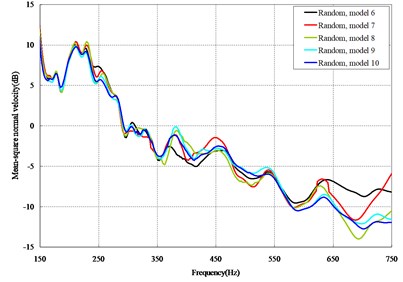
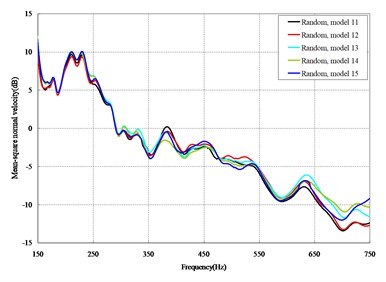
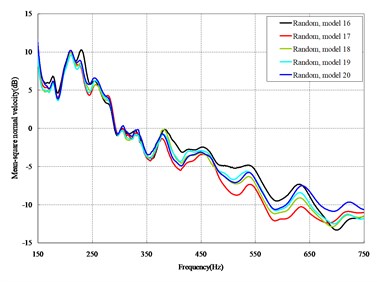
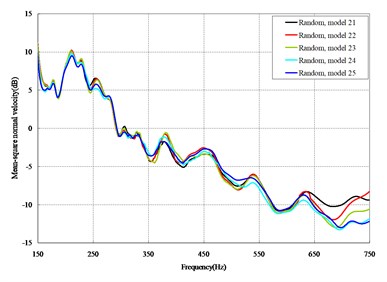
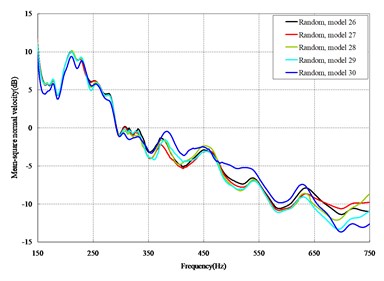
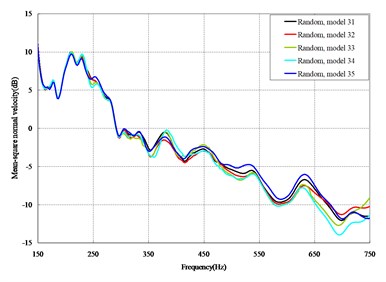
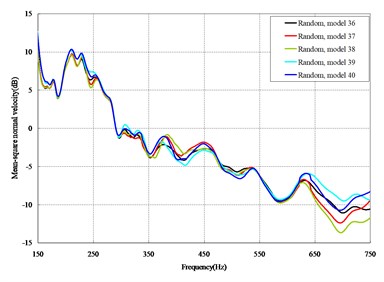
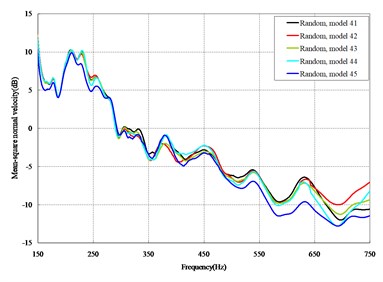
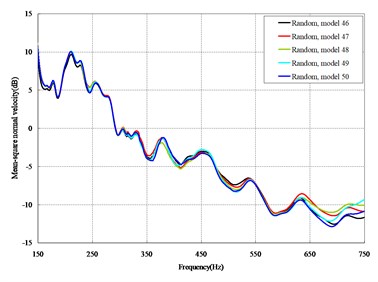
Fig. 4Comparison among 50 models under vertical loads

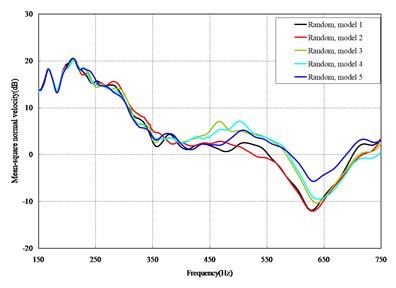
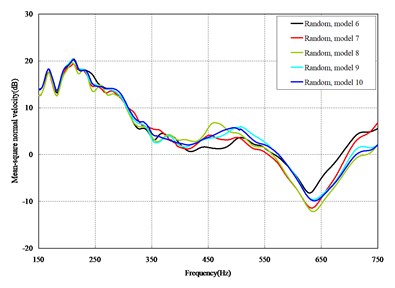
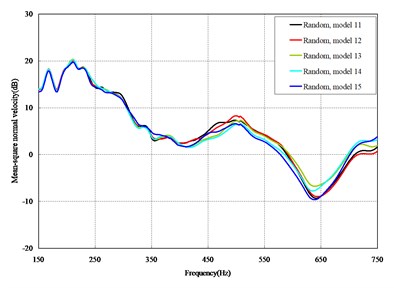
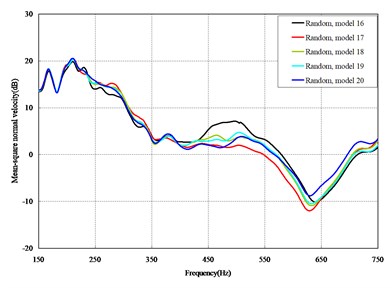
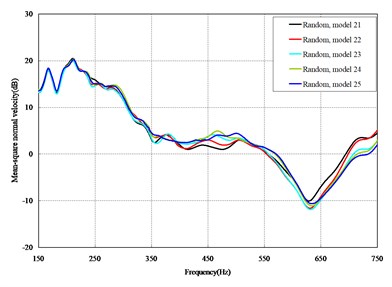
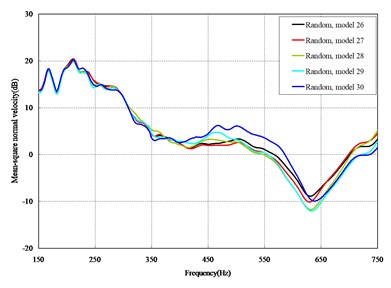
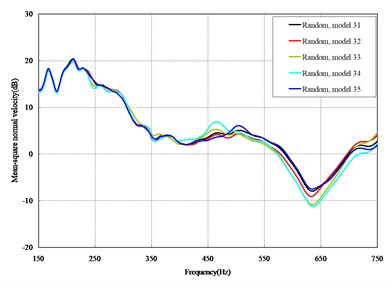
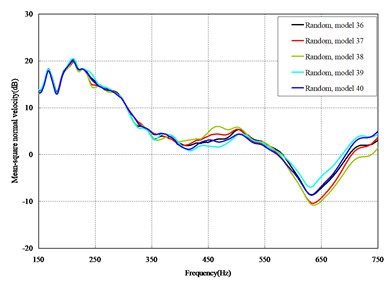
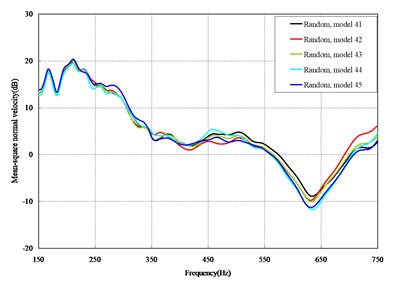
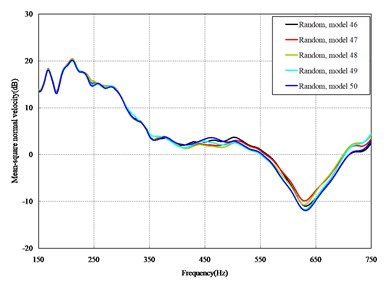
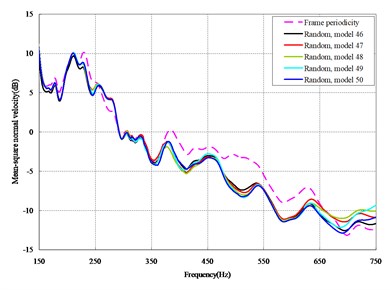
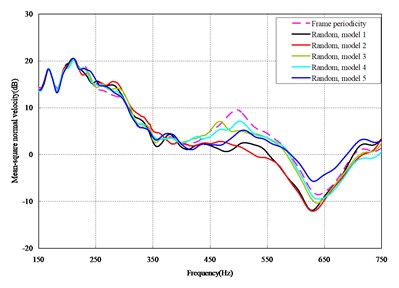
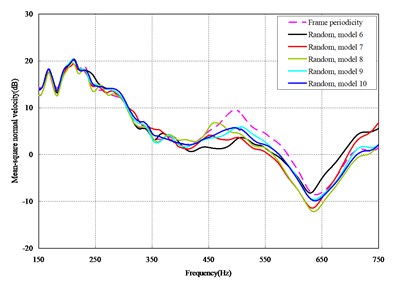
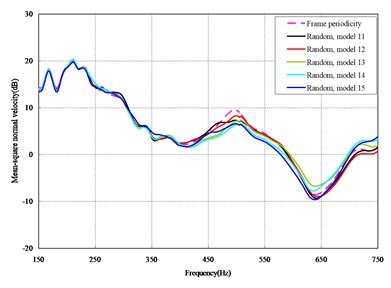
The mean square normal velocity of the 50 cylindrical shells with random frame spacing arrangements introduced in Section 3.1 were compared and analyzed. It can be seen that before 700 Hz, the curves of vibration response cross-connect, and, on the whole, the difference among the results of the 50 cylindrical shells is small, except for some parts, which are shown in Figs. 3 and 4. Fig. 3 plots the vibration response of the case in which axial exciting force acting on the base of the floating raft is applied and Fig. 4 that of the case in which vertical exciting force acting on the base of the floating raft is applied.

The vibrations of the cylindrical shell with frame periodicity and that with a random frame-spacing arrangement were compared, as shown in Figs. 5 and 6. Fig. 5 plots the vibration response of the case in which axial exciting force acting on the base of the floating raft is applied and Fig. 6 that of the case in which vertical exciting force acting on the base of the floating raft is applied.

Fig. 5Comparison between periodic and random arrangements under axial loads

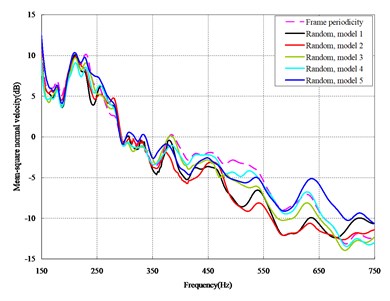
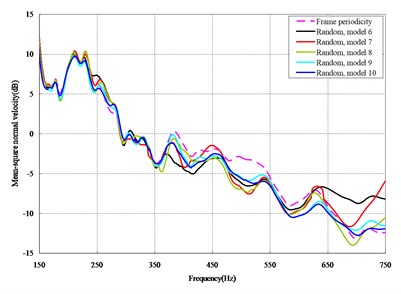
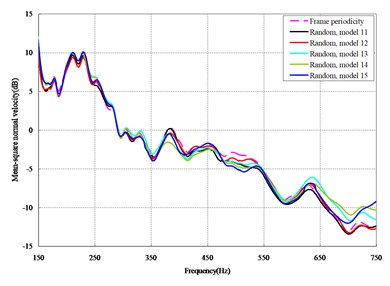
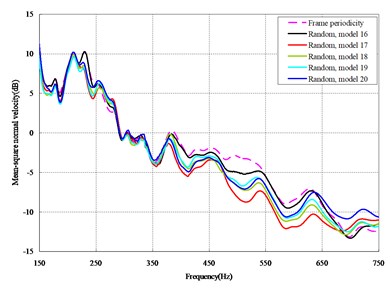
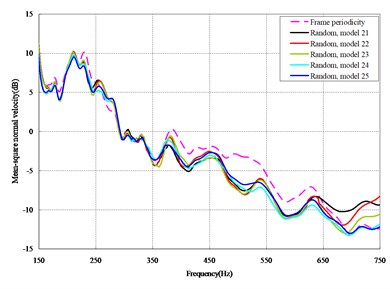
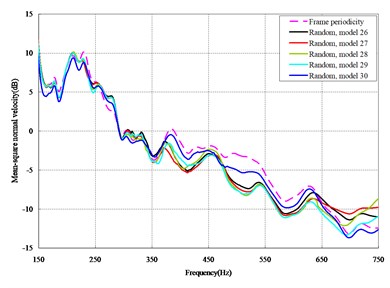
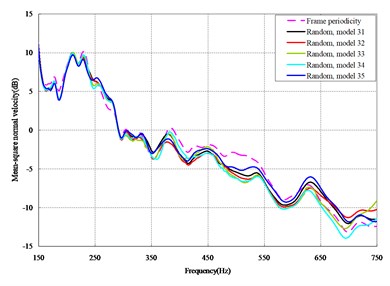
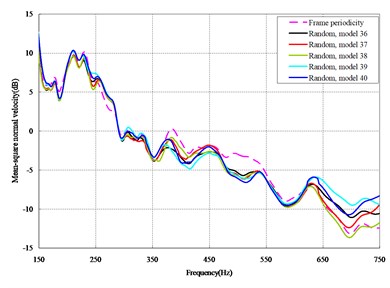
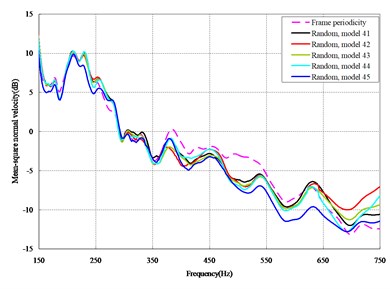
From the results in Figs. 5 and 6, the following conclusions can be drawn:

1) For the finite-length cylindrical shell, when the frequency of the exciting force is less than 350 Hz, the difference in the vibration response between the cylindrical shell with frame periodicity and that with frame aperiodicity is not obvious. The reason is that in the low-frequency band the wavelength of the structural wave is relatively longer, so the method of arranging the frame spacing has little influence on the total vibration of the cylindrical shell. However, with increasing frequency, the wavelength of the structural wave becomes relatively shorter, and thus, the influence of the method of arranging the frame spacing on the total vibration of the cylindrical shell becomes increasingly more obvious. When the frequency of the exciting force is in the range of about 350-600 Hz, compared with the periodic arrangement of the frame spacing, the aperiodic arrangement of the frame spacing can decrease the vibration of the cylindrical shell with a maximum reduction of up to 9 dB.

2) For the finite-length cylindrical shell, the aperiodic arrangement of the frame spacing can decrease the vibration of cylindrical shell, but the effect exists only in some narrow frequency band, generally at medium-high frequency.

Fig. 6Comparison between periodic and random arrangements under vertical loads

3) Changes in frame spacing mainly affect the propagation of the structural waves between adjacent frames. Taking model 1 as an example, the first 4000-order modes were obtained through numerical simulation, and it can be seen that when the natural frequency is less than 350 Hz, the structural wavelength on the shell plate exceeds the distance between adjacent frames, as shown in Fig. 7(a) and Fig. 7(b), so when the frequency is less than 350 Hz, the change in frame spacing has little effect on vibration. When the natural frequency is greater than 350 Hz, the vibration on the shell plate is dominated by the vibration between adjacent frames, and the structural wavelength is usually less than the distance between adjacent frames, as shown in Fig. 7(c)-7(f), so when the frequency is greater than 350 Hz, the frame-spacing changes affect the vibration, but when the frequency exceeds 600 Hz, the vibration on the shell plate is mainly local vibration, as shown in Fig. 7(g), the effect of frame-spacing changes on vibration is reduced.

Fig. 7Structural wavelength vs. frequency

a) 250.59 Hz

b) 312.95 Hz

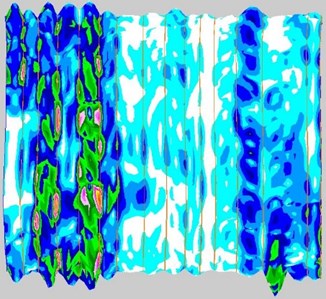
c) 350.20 Hz

d) 450.15 Hz

e) 550.33 Hz

f) 590.61 Hz

g) 610.69 Hz

4.1. Experimental models

There were two experimental models, which were represented by Model s1 and Model s2. The structural scale of both models was the same, only the position of the frames was different. The models are made of steel material, and their main dimensions and material parameters are shown in Table 1.

Both models were arranged along the axial direction of the shell with 6 frames, of which Model s1 was equally spaced, the frame spacing was 700 mm. On the base of Model s1, design the random arrangement of frame spacing. The probability density of the position of a particular frame $x$ satisfies Eq. (1), in which $d=$ 0.7 m, $\mathrm{\Delta }x$ equal to 30 % of the frame spacing of the cylindrical shell with frame periodicity, $\mathrm{\Delta }x/d=$ 0.3. There were 6 frames for each cylindrical shell; $n=$ 6, that is to say, 7 frame spacings were generated by the random method, with each measuring 0.5-0.9 m in length. Due to the axial length of the experimental models are shorter compared to the models in Section 3.1 of my paper, thirty groups of frame spacings were generated; in other words, 30 framed cylindrical shell models were made, named models 1-30, as shown in Table 2. Obviously, the arrangement of frame spacing is aperiodic. The vibration responses of the cylindrical shells with frame periodicity (Model s1) and frame aperiodicity (models 1-30) were separately calculated by FEM in air, and MSC.Patran was used to build the models of the framed cylindrical shell, therefore the accuracy of the calculation was guaranteed. The frequency band of the exciting force is 1-1000 Hz. On the base of the vibration responses, the mean square normal velocity was obtained by Eq. (3). Calculate the average area enclosed by the “mean square normal velocity” curve and the “frequency” axis for all models according to the following Eq. (5), and the result is expressed in $\stackrel{-}{V}$. $f_2$ and $f_1$ in the Eq. (5) represent the upper and lower limits of the integration, respectively, where $f_1=$ 1 Hz, $f_2=$ 1000 Hz:

Take the logarithm of $\stackrel{-}{V}$ to get $L_{\stackrel{-}{V}}$, and $L_{\stackrel{-}{V}}$ represents the total vibration level of the model:

The total vibration level of Model s1 is 10.90 dB, and the total vibration levels of the models in Table 2 are shown in Table 3. It can be seen that the vibration levels of all models in Table 3 are smaller than Model s1. In Table 3, the total vibration level of Model 23 is the smallest, therefore, based on the frame spacing of Model 23, the experimental model with the aperiodic frame-spacing was processed. For the convenience of processing, the frame spacing of Model 23 is fine-tuned, and the experimental model shown in in Fig. 8 is obtained, named Model s2.

Fig. 8Aperiodic frame spacing of Model s2

To facilitate the installation of the exciter, the cylindrical shell was hoisted horizontally (as shown in Fig. 9(a)). The exciter generated a sinusoidal excitation force $F$, which acted on the cylindrical shell through the excitation rod (as shown in Fig. 9(c)). To simulate the free boundary conditions, the cylindrical shell was suspended at both ends, and connected to the hoisting equipment with a soft rope (as shown in Fig. 9(b)).

In this experiment, the acceleration sensor was used to measure the vibration response at each typical position of the structure, and the arrangement of the acceleration sensor mainly considered two factors: one was to ensure that one structure wave or half of the structure wave between the frames could be measured, and the other was that the sensor was densely arranged on the structure near the vibration source. The arrangement of the acceleration sensors was shown in Fig. 10.

Fig. 9Hoisting of model

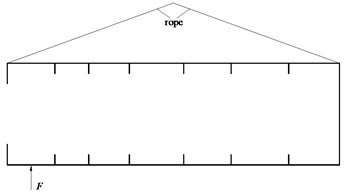
a) Design sketch of hoisting model

b) Experimental model

c) Installation of vibration exciter

Fig. 10Sensor arrangement of models

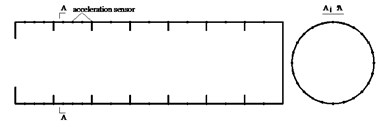
a) Sensor arrangement of Model s1

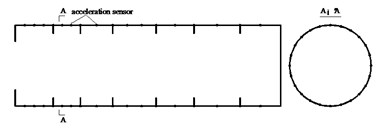
b) Sensor arrangement of Model s2

4.2. Experimental validation

The vibration response of Model s1 and Model s2 was obtained experimentally, and the mean square normal velocity of the cylindrical shell was calculated by Eq. (3), which was compared with the result by the numerical method, as shown in Fig. 11. It can be seen that the experimental and the numerical results were in good line.

Fig. 11Comparison between experimental results and numerical results of mean square velocity

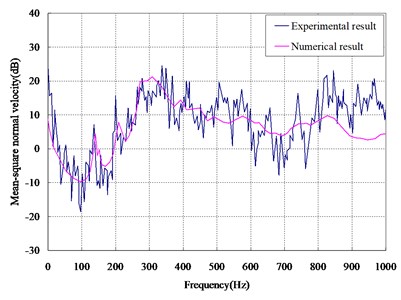
a) Result of Model s1

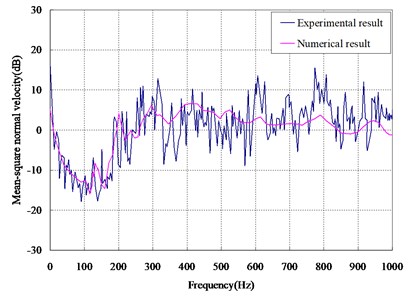
b) Result of Model s2

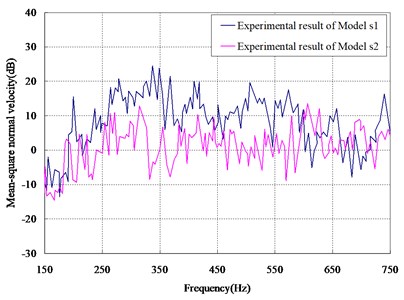
Comparing the experimental results of Model s1 and Model s2, as shown in Fig. 12, it can be seen that in some frequency band (e.g., 220-440 Hz, 460-600 Hz), the aperiodic frame-spacing arrangement can reduce the vibration of the cylindrical shell.

Fig. 12Comparison between experimental results of two models