Numerical study of shear thickening fluid with distinct particles dispersed in carrier fluid

1. Introduction

As the world is changing rapidly in many aspects and so humans. If we see the past, then maximum battles were due to land and water. So, for that, we need civil, military structures and updated systems which overcome the impact due to things which were used during the encounter. There are so many energy absorbing materials which have been considered in order to overcome the impact or shock loading. Shear thickening fluid (Polypropylene Glycol 400 and sand) [1] is a portable solution that when sheared increases its viscosity so the more stress applied to it the more resistance it gives to that.

Shear thickening fluid (STF) could possibly be used to fortify the resistance of army garment and body armor against ballistic thread [2] and puncture [3]. Zip lock bags of STF on soldier and it would be nice and flexible when he is walking around but then if a projectile come and hit on STF armor it would turn hard and reflect he projectile. In the past, experimental analysis was a common research approach in studying STF but now availability of advanced software and machines makes it logical to do modelling and study numerically to further understand the physics and mechanisms of STF [4].

In Lagrangian, a fluid particle is being followed at each point the fluid properties are then determine as the fluid particle move about. But in Eulerian approach a frame is fixed at a particular point in space during a fluid flow and noting that characteristics of the particles as they pass through the frame [5]. Stokesian dynamics methods [6], Dissipative particles dynamics [7] and the Lagrange multiplier fictitious domain method are other computer models which are now used to study fluid characteristics. This study depicts us the shear thickening effect when we use both Eulerian and Lagrangian models [8]. By using these models, the study shows us the effects of various factors that are linked with rigid body particles on shear thickening. Such factors comprise of particle size, shape, volume friction, distributions, and many more the next section offers a brief analysis of Shear Thickening Fluid (STF), which is then classified by using the description of different things like numerical modeling and analysis. Thereafter, the numerical results and discussion are presented followed by results obtained after the computational studies.

2. Review of STF

A fluid in which the shear stress is directly proportional to the rate of shear strain is known as Newtonian fluid:

where $\tau$ – shear stress, $\mu$ – viscosity of a fluid, and $du/dy$ – strain rate.

Fig. 1 shows on the $Y$-axis the shear stress and plotted against the $X$-axis which is rate of shear strain or the velocity gradient. As the straight line goes through a zero is a Newtonian fluid that follows the Eq. (1). Also, there are many type of fluid that do not behave like Newtonian fluid and the study of these kind of fluid is called rheology such fluid comes under non-Newtonian fluid.

According to the power-law model viscosity and shear strain rate can be expressed in the mathematical expression of for non-Newtonian fluids:

where $n$ – flow behavior index, $K$ – flow consistency index.

The mathematical expression of the apparent viscosity in term of shear strain rate can be written as:

For a Newtonian fluid type, the $K$ (flow consistency index) is equivalent to fluid viscosity, and the flow of behavior index $n$, is one. For the STF $n$ is greater than 1. Fig. 2 shows the relation where a Newtonian Fluid relationship is summarized. STF is the example of dilatant material which comes under non-Newtonian fluid. The dilatant material like sand, ethanol, mercury can be dispersed in carrier fluid e.g. water or Polypropylene Glycol (PPG400) [9].

Fig. 1Shear stress Vs shear strain rate

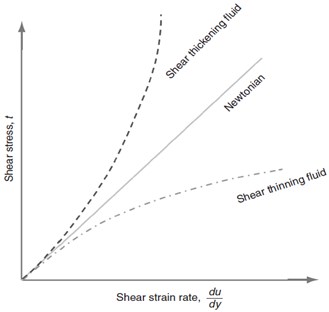
Fig. 2Relation between flow consistency index (Pa sn) and shear stress (Pa)

3. Numerical modeling and analysis

3.1. Modeling of STF

Eulerian approach is mostly used to model the STF in two phase or multi-phase. The Lagrangian approach at the particle-level was used to examine the characteristics of the STF in this study, based on contact with a Eulerian carrier fluid. In this study individual particle was focused for numerical analysis. ANSYS CFX Rigid Body Solver was used for the geometry modelling, meshing, setup, solution and results. Also, ANSYS CFX was used to optimize each rigid body movement when it subjected to shear loading condition.

Fig. 3Geometry of shear thickening fluid model

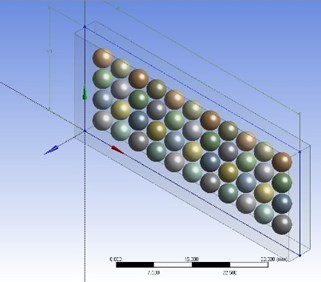
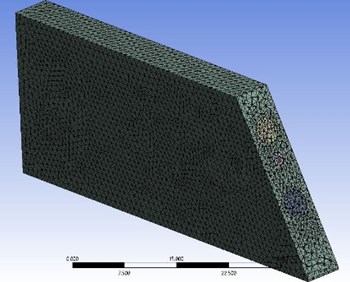
Fig. 4Meshing of silica and fluid domain in STF model

3.5. Boundary conditions

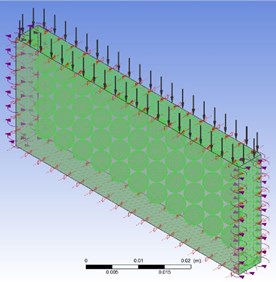
In the set-up part we defined the boundary conditions. The rectangular box was considered as the fluid domain and spherical ball was considered as sand particles. Spherical balls are placed inside the carrier fluid. Upper wall of the fluid domain was considered as inlet and bottom wall was considered as no slip wall. Right and left wall was defined as transitional periodicity interface. Front and back wall was considered as boundary of the fluid domain. In the analysis command we chosen the 2 second times for transient simulation at 0.2 s time step. Also, The Rigid Body Solver was used for silica particle interaction with carrier fluid.

Fig. 5Boundary condition and finite element meshing

4. Results and discussion

All the calculation was done by using velocity magnitude 2 m/s. Inlet face of the fluid domain was subjected to shear velocity of 2 m/s. The acceleration was calculated 0.195 m/s² under this velocity with respect to time. Parameter like viscosity, shear strain rate, pressure gradient, velocity distribution and mass flow were calculated in this study. Viscosity of STF increase with respect to shear strain rate. As the shear strain rate increase viscosity of STF initially decreases and after certain point it raises. This characteristic makes the STF future Body armor material. Pressure gradient decreases along $Y$ direction as the velocity increases. Momentum boundary flow on fluid domain also increases with respect to time.

Fig. 6Shear strain rate and viscosity distribution for flow velocity of 2 m/s

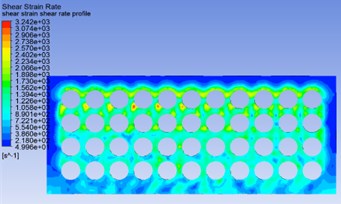
a)

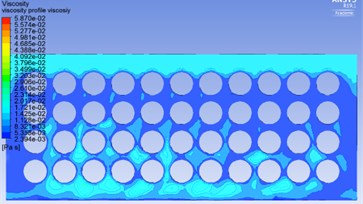
b)

Fig. 7Pressure gradient distribution and velocity profile distribution at 2 m/s

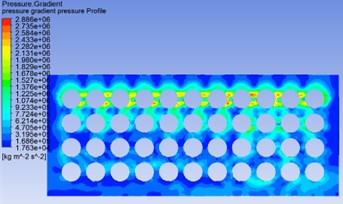
a)

b)

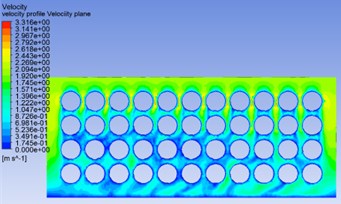
Fig. 8Velocity profile along Y-direction

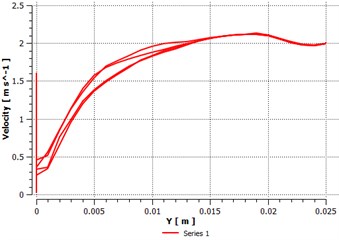
Fig. 9Viscosity vs. shear strain rate

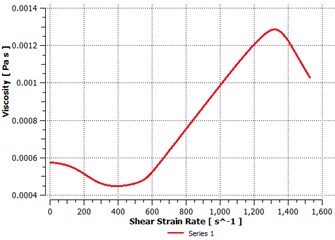
Fig. 10Momentum of fluid flow vs. time

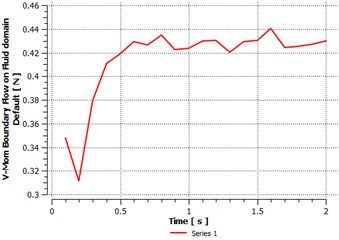
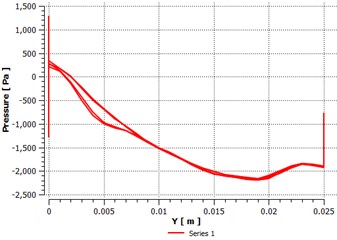
Fig. 11Pressure distribution along Y direction

5. Conclusions

The numerical simulation analysis was led by modeling the separated sand particles and base fluid interaction. The important particle parameter was studied by using the Lagrangian and Eulerian approach, that could influence the execution of STF. By applying higher acceleration and velocity to the STF domain higher shear thickening effects could be achieved, Also higher concentration of sand particles in base fluid effect the viscosity of the STF. This numerical simulation proposed that sand particles could further improve the viscosity of STF. Improve viscosity leads to the improve shear thickening result of dilatant fluids, although a further study is required for the non-linear response at lower shear strain rates. Favorable outcome in the simulation of the shear thickening effect would motivate for more upgraded and enhanced Shear thickening fluid design.