Estimation of wear rate in dual phase steel on the basis of the load sharing between constituent phases

1. Introduction

Wear Behaviour of a system is governed by atmosphere, external variables and mating material selection. Hence, it needs to be fully understood before developing any theoretical model. In the beginning of relative motion, the rubbing surfaces produce a considerable amount of wear due to the presence of asperities. However, after a short period of running-in, mating surfaces attain better compatibility resulting in increased real area contact and reduced rate of wear or a change of wear mechanism [l-3], such as to a mild or oxidational wear [4]. Tailored two phase materials like metal-matrix composites (MMCs) are widely used in industries for different components like pistons, brakes in auto-mobiles and aircraft [5] because of their excellent mechanical properties and wear resistance. The wear of materials involving two or multiple phases has been studied by several researchers [l-4, 6] and several models have been proposed for estimation of wear rates [3, 7-9]. However, no such models are available for dual phase (DP) steels which is also a typical two-phase material consisting of hard martensite islands embedded in a relatively softer phase of ferrite. Recently few studies have been conducted to analyze the tribological potential of DP steels and a model for oxidational wear has been proposed by the authors [10] to investigate the wear behavior of DP steel by modifying the models of Archard’s [11] and Quinn [12].

In the light of above, the main objective of present paper is to develop a new model for the estimation of wear rate in a typical two-phase material like DP steel based on the sharing of load between constituent phases and their distinct wear behavior. The model has been checked by the experimentally observed wear rates of Armco iron and fully martensitic steel (FMS), simulating the ferrite and martensite phases, respectively in DP steel. The model is expected to helpful in predicting the wear rate in both the run-in and the steady state for two phase materials. Hence, one may tailor the microstructure of DP steel for a given in-service wear performance of these steel.

2. Archard’s law and wear in two phase material

Archard [11], in his wear model for single phase material has concluded that wear rate is given by:

where $V$ is the volume of the material worn after sliding through a distance $S$ and $K_1$, called the wear coefficient. $L$ is the normal load and $H$ the hardness of the softer of mating material. In the present work, it has been explored whether the wear rate in two phase materials could be estimated in terms of wear behavior of the constituent phases i.e., ferrite and martensite, in the framework of Archard’s law given in Eq. (1). For DP steel, it is assumed that the wear rate is the sum of wear rates of its constituent phases and thus, the wear rate of DP steel may be expressed as:

where, ${\left(V/S\right)}_{DP}$ is the wear rate of DP steel, $K_f$ is the wear coefficient of ferrite in DP steel and $K_m$ is the wear coefficient of martensite in DP steel. $H_f$ and $H_m$ are the microhardness of ferrite and martensite in DP steel. $L_f$ and $L_m$ are the normal contact loads shared by ferrite and the martensite islands, respectively, in DP steel. the real areas of contact. Based on earlier work Eqs. (10), the real areas of contact in ferrite, $A_{rf}$ and martensite $A_{rm}$, may be estimated as:

Using the values of $A_{rm}$ and $A_{rf}$ one may arrive at the estimates of loads shared by the ferrite matrix ($L_f$) and the dispersed martensite ($L_m$) island as:

By substituting the values of $L_f$ and $L_m$ in Eq. (2) the expression for the wear rate in a dual phase steel becomes:

The values of $H_f$ and $H_m$ are experimentally determined. The volume fraction of martensite, $V_m$, is estimated from the microstructure by point counting technique. The wear rate in the dual phase steel may thus be estimated using Eq. (7) by putting the values of wear coefficients of the constituents known a priori by carrying out wear tests on ferrite (Armco iron) and martensite (FMS) samples.

3. Experimental procedures

Intercritical annealing heat treatment was performed on cylindrical (30 mm×4.0 mm Ø) specimens of 0.42 pct carbon steel using a vertical tube furnace at 740 °C for 2.0, 2.5, 3.0 and 3.5 minutes to develop dual phase steel containing four different volume fractions of martensite. Detailed procedure in respect of development of dual phase steel and their metallographic characterization is given elsewhere [13, 14]. Wear tests were done using a pin-on-disc machine at loads of 14.7, 19.6, 24.5, 29.4 and 34.3 N and at a constant sliding velocity of 1.15 m/s. Specimens of Armco iron and fully martensitic steel (FMS) were also tested under similar conditions. The wear rate was measured by mass loss of the specimens at different intervals. A detailed description of wear testing has been described earlier [15]. Each test was conducted thrice under a certain condition of load and speed and the average of the data has been used for the analysis.

4. Results and discussion

4.2. Wear characteristics

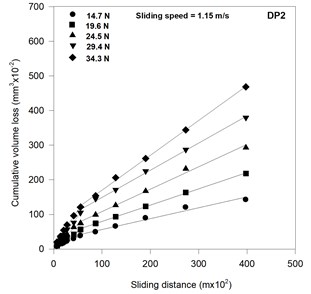
Fig. 2 presents the variation of cumulative loss with sliding distance in DP2 steel under different normal loads and a constant sliding velocity of 1.15 m/s. Cumulative wear volume increases linearly with increasing distance of sliding as seen from Fig. 2. The slope of the variation is observed to change after sliding through 5.53 km. Therefore, the wear volume distance relationship is represented by two linear segments indicating the run-in and the steady state of wear [13, 16, 17]. The wear volume also increases as the load increases as evident from Fig. 2. A similar trend has been observed for other steels and Armco iron investigated in the present study. The wear rates for run-in and the steady state in DP steels have been estimated from the slope of linear square fit lines of the cumulative wear volume vs. sliding distance curves. The wear rate corresponding to the steady state is less than that observed in the run-in stage of wear as can be seen from slope of the respective least square fit lines given in Fig. 2. Table 1 shows the wear rates corresponding to both the run-in and the steady state of wear for all the materials investigated in the present study.

Fig. 1Microstructure of dual phase steel, DP2, with dark islands of martensite in white matrix of ferrite

Fig. 2Variation of cumulative wear volume with sliding distance in DP1 steel containing 51 pct martensite

The wear rates in run-in as well as steady state have been estimated on the basis of (i) estimated load sharing between constituent phases and (ii) the observed wear coefficients of Armco iron and martensitic FMS by using Eq. (7). The estimated and observed variations of wear rate with normal load in run-in stage of wear for dual phase steels DP1, DP2, DP3 and DP4 are shown in Figs. 3(a) to (d), respectively. The estimated wear rate increases linearly with the load for all the DP steels and shows a good matching with the observed wear rate at lower loads but has increasingly higher difference with the observed values at increasing loads. The slope of the variation of wear rate with normal load decreases with increasing volume fraction martensite for both the estimated and observed variations as can be seen from Figs. 3(a) to (d). The estimated and observed values of wear rate become closer at higher loads with increasing martensite volume fraction.

The calculated (using Eq. (7)) and observed variations of wear rate with normal load in the steady state for dual phase steels DP1, DP2, DP3 and DP4 containing 42, 51, 59 and 72 pct martensite are shown in Figs. 4(a) to (d), respectively. The slope of the variation of wear rate with normal load decreases with increasing volume fraction martensite for both the estimated and the observed variations. The estimated wear rates show a good matching with the experimentally observed wear rates at lower loads but have increasingly larger difference with the observed values at increasing loads. However, the difference between estimated and observed wear rates decreases as one moves to higher loads and g martensite content. The difference between estimated and observed wear rates is much less in the steady state than run-in stage of wear as seen from Figs. 3(a) to (d) and Figs. 4(a) to (d). In DP3 and DP4 steels the least square fit lines for calculated and experimental wear rates appear to cross at some intermediate load with values of calculated and experimental wear rates falling in the same band.

The difference in the calculated and the observed wear rates may be attributed to the flow of the softer phase of ferrite over the hard martensite islands resulting in easily oxidized junctions of low shear strength while maintaining the same real area of contact. The higher rate of wear of this ferrite over that of martensite might have led to higher observed wear rates. This is evident from the much higher rate of wear observed for the Armco iron as compared that for the FMS in the present study (Table 1). As the martensite volume fraction increases, the flow of ferrite gets restrained and thereby a better matching between the experimental and the calculated results is observed because the sliding surface has both ferrite and martensite in amounts as presumed in the calculation. At lower loads, the flow of ferrite is not significant and therefore, a better matching of the experimental and the calculated results is observed.

Fig. 3Variation of the calculated and the experimental wear rates with normal load in the run in stage of wear in DP steels

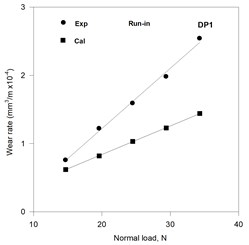
a)

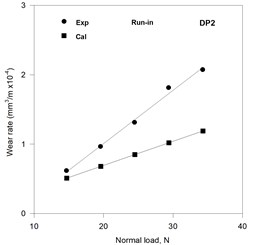
b)

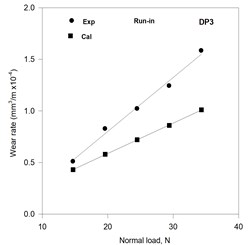
c)

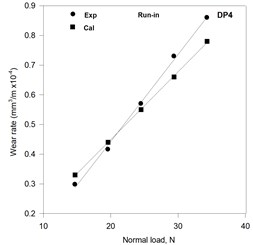
d)

Fig. 4Variation of the calculated and the experimental wear rates with normal load in the steady state of wear

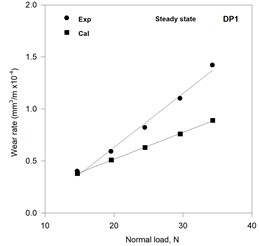
a)

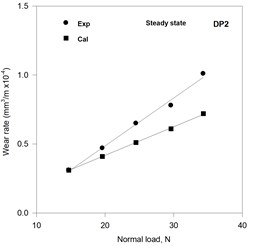
b)

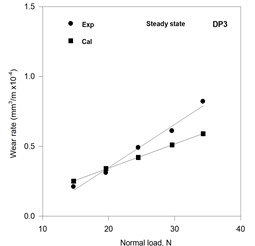
c)

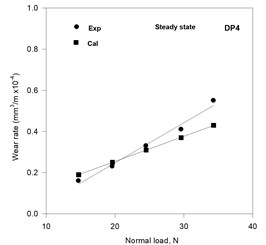
d)

However, with increasing load the flow of ferrite becomes significant resulting in higher observed wear rates in steels having a relatively lower martensite volume fraction. But an increase in the martensite volume fraction inhibits the flow of ferrite and the wear rate is also contributed by the oxidative wear of martensite, which wears at a relatively lower rate. Therefore, a better matching between the estimated and the observed wear rates is obtained at higher martensite volume fractions as it could be observed from Fig. 3(d) and Fig. 4(c) and 4(d).

5. Conclusions

1) A simple model has been proposed to predict the wear rate in dual phase steel based on (i) estimated load sharing between the constituent phases and (ii) the observed friction and wear behavior of Armco iron and fully martensitic steel.

2) The wear rates predicted by the proposed model have been found to match with experimentally observed wear rates fairly well in the regime of lower loads but show a little higher value at relatively higher loads used in the present study. However, the matching is better even at higher loads with the increasing content of martensite. The observed mismatch has been attributed to the flow of the softer phase of ferrite over the hard martensite islands and the higher rate of wear of this ferrite over that of martensite.

3) A better matching between the estimated and the observed wear rates obtained at higher martensite volume fractions has been credited to the restricted flow of ferrite and the contribution from the oxidative wear of martensite, which wears at a relatively lower rate.