Traffic seismicity effect on monumental buildings – results of case studies

Valašková, Veronika; Papán, Daniel; Papánová, Zuzana

doi:10.21595/jme.2018.20413

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: 31 December 2018

Check for updates

Traffic seismicity effect on monumental buildings – results of case studies

Veronika Valašková¹

Daniel Papán²

Zuzana Papánová³

^{1, 2, 3}University of Zilina, Faculty of Civil Engineering, Department of Structural Mechanics and Applied Mathematics, Univerzitna 8215/1, 010 26 Zilina, Slovak Republic

Corresponding Author:

Veronika Valašková

Cite the article Download PDF

Downloads 1506

WoS Core Citations 2

CrossRef Citations 3

Abstract

Traffic seismicity is the current phenomenon, and the impact of traffic seismicity on monumental buildings has significant importance. This paper discusses the results of three different case studies, where the impact of traffic seismicity is important. These buildings were selected as case studies, due to a short distance from the source of the vibrations, respectively the traffic lines. All these three buildings are historically significant in their region. The contribution is focused on experimental results and on numerical analysis of building structures. Works of this and similar character supports to the establish and determinate limit criteria in assessing the dynamic response to the effects of traffic seismicity. For this reason, it is important to realize a great amount of measurements, that such conclusions can be expressed. This requirement is based on insufficient legislation and standards in technical field in Slovakia.

1. Introduction

Traffic seismicity on lower classes of roads have negative influence on monumental buildings, especially in the case redirecting of heavy international traffic to these routes. These classes of roads do not have a high priority in maintenance and reconstruction. Many of these problems have to solve city and general councils, which do not have the necessary funds for their reconstruction and preservation. The consequence of this problem increasing due to the unevenness. All these factors resulting to increasing effects of traffic seismicity in general. Therefore, it is necessary to increase the focus of this problematic especially in the towns with adjacent highways. Wholesale, historic buildings are situated near heavy traffic roads, despite the negative factors, because traffic has not been important in the past. The traffic intensity has increased at the present time. It is important to pay attention to this research field and analyse the impacts of traffic seismicity. The use of the random process theory to predict the level of ground vibration in the closeness of roads via calculation of the spectrum of vibration at half space point is possible by the two principal ways. First way is computer implementation of the theoretical expression for the road roughness spectrum, the vehicle mass distribution spectrum and a model of vehicle dynamics and the frequency response function (FRF) of the ground by a method involving integral transform. Second way is using average response force spectrum derived from experimental data for authorized roadway category with corresponding road profile and the FRF of the ground and calculate spectrum vibration at investigative point. The analysed case studies of investigated buildings have the significant importance. The monumental civil structures are also more sensitive to all external factors of load changes. The maintenance of these monuments is often insufficient and therefore we should perceive them as a more important building than ordinary new designed (reinforced concrete, steel). The presented case studies were selected for these reasons [1, 2].

2. The FEM frequency analysis of the monumental building

These case studies present the frequency domain analysis of one monumental building. Computational models of case studies were developed in Scia engineering software. This software as a numerical solver uses the finite element method (FEM) – deformation variant designed for static and dynamic analysis of structures and their proposal to appropriate standards. Scia engineering used advanced technique to solve and analyse physical problems arising in many fields of science and engineering. This program is a full-fledged software integrated with ease-of-use but powerful functions for pre- and post-processing as well as for FEM processing. The various computational aspects and concepts involved in FE modelling can be easily understood through computational simulation. Its pre-processing capability includes the most advanced 2 and 3-dimensional mesh generation techniques [3].

2.1. The solving of dynamic problems in FEM

At the dynamic application works on the construction in time (order of seconds) variable load. Due to flywheel forces resulting from the accelerated motion of the mass, causes the dynamic response of the system. The equation of equilibrium conditions has the form:

1

[K] \{r (t)\} = \{F (t)\},

where the external load vector $\{F (t)\}$ is accompanied by inertial $\{F_{m}\}$ and damping forces $\{F_{c}\}$ operating in the construction, which is based on the d'Alembert principle dependent on acceleration $\{\ddot{u}\}$ respectively, speed $\{\dot{u}\}$ :

2

\{F (t)\} = \{F_{b}\} + \{F_{m}\} + \{F_{c}\},

\{F (t)\} = \int_{V}^{} {[N]}^{T} (\{b\} - ρ \{\ddot{u}\} - κ \{\dot{u}\}) d V = \int_{V}^{} {[N]}^{T} (\{b\} - ρ [N] \{\ddot{r}\} - κ [N] \{\dot{r}\}) d V,

while:

3

\{F_{m}\} = - \int_{V}^{} ρ {[N]}^{T} [N] d V \{\ddot{r}\} = - [M] \{\ddot{r}\},

\{F_{c}\} = - \int_{V}^{} κ . {[N]}^{T} . [N] . d V . \{\dot{r}\} = - [C] . \{\dot{r}\},

where: $\{\dot{r}\}$ is velocity element vector, $\{\ddot{r}\}$ is acceleration element vector, $ρ$ is specific weight, $κ$ is damping parameter, $[M]$ is matrix of mass element, $[C]$ is matrix of dumping element. Substituting express equation of motion shaped element:

4

[M] \{\ddot{r}\} + [C] \{\dot{r}\} + [K] \{r\} = \{F\} .

In the case of seismic loads is the structure located on moving weighted subsoil loaded with inertial load, operating in the different discrete points with a concentrated mass:

5

\{F\} = - [M] \{\ddot{r_{b}}\},

where $\{\ddot{r_{b}}\}$ is acceleration vector at level of foundation.

In principle, we can solve the equations of two methods: Method of modal analysis – solution in the frequency domain or the method of direct integration at the time - the solution over time [4].

These systems of equation solve the dynamic response of the system in the time domain. But for the buildings, the dynamic properties of the systems that are their natural frequencies and shapes of natural vibration are very important. They are solved with a method, which transforms the solution of continuous systems and systems, to solving systems with the finite degree of freedom. The basic properties that be known for creating any computational model are the mass and stiffness of the element. These mathematical solutions are directly integrated in Scia Engineer software. This software was used in numerical calculations on dynamic models of buildings, in Case Studies.

3. The experimental analysis in frequency domain

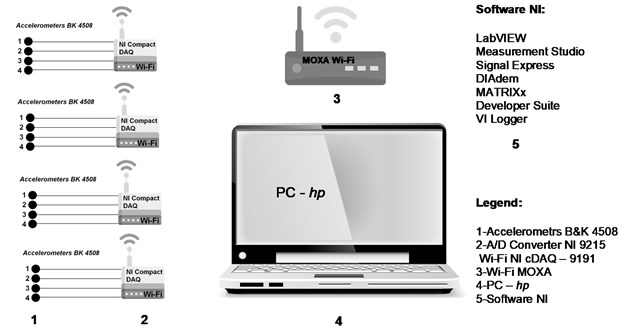
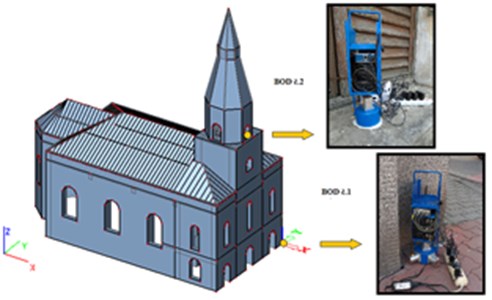
The dynamic response of our case studies due to the random excitement was measured on two observed points of the three axes accelerometers (input – near road and in the building). The frequency range of accelerometers sets was 1/4000 Hz (Brüel-Kjaer). Recorded response was in vertical and horizontal direction. Dynamic response in the observed points were measured in the form of vibration velocities (m/s), in three orthogonal directions $x$ , $y$ , $z$ .

The measuring unit consisted of:

• Piezoelectric accelerometers BK 4508 (Bruel-Kjaer),

• Integration amplifier BK-2693-014 (Brüel-Kjaer), measuring PC/hp Notebook,

• NI cDAQ™-9191NI CompactDAQ One-Slot Wireless Chassis,

• Moxa AWK-3121 With NI CompactDAQ.

Fig. 1Block diagram of the recording and measuring line

Dynamic response was evaluated using spectral and amplitude analysis. The Sigview [5] software package was applied for the signal processing results of the experimental measurements. This software is developed for digital data signal processing of the measured records mainly noise and vibration. In the amplitude analysis the simple formulas for numerical signal are used in this evaluation system. For the natural frequencies identification Fast Fourier Transformation (FFT) and its applications implemented in the Sigview system were used. The summarized results of the dynamic experimental investigation of all case studies are presented in Table 1, 2 and 3. Dynamic response of these historical buildings due to traffic seismicity load were analyzed in characteristic points (highest part of towers). The distance from the excitation lines are in C.S. Nr. 1. 1 m, C.S. Nr. 2. 2 m and C.S. Nr.3. 12 m. Dominant frequencies in the traffic seismicity response spectra determinate experimental identified natural frequencies. In the dominant frequency broadband, the Root Mean Square (RMS) value specifies the magnitude of the traffic seismicity effects on the buildings [6, 7].

The RMS values presented in Table 1, 2 and 3. (bold) were identified due to passing of the heaviest vehicle in the monitored cycle. It was signed as the seismic process with highest magnitude affecting on the historical building.

3.1. Spectral functions – basic principles

In order to solve dynamic response obtained from measurements presented in case studies the spectral analysis was applied. For the solution of a random phenomenon is called to be analysed as stochastic process (action). The character of the analysis is divided to deterministic (numerical solution – capture 2) and stochastic analysis (measurement results).

Properties of random processes were evaluated on followed basics:

Time domain (time histories) check, effective value of the relationship:

6

σ_{x} = R M S = x_{e f} = \sqrt{\frac{1}{T}} \int_{0}^{T} x {(t)}^{2} d t .

Auto correlation function:

7

R_{x x} (τ) = \underset{T \to \infty}{l i m} \frac{1}{T} \int_{0}^{T} x (t) x (t + τ) d t .

Cross correlation function of the processes $x (t)$ , $y (t)$ :

8

R_{x y} (τ) = \underset{T \to \infty}{l i m} \frac{1}{T} \int_{0}^{T} x (t) y (t + τ) d t .

Sectral (spectral power distribution of the frequencies) power spectral density $G_{x x} (f)$ :

9

G_{x x} (f) = 2 \int_{- \infty}^{\infty} R_{x x} (τ) e^{- i 2 π f τ} d t .

Coherency function:

10

γ_{x y} {(f)}^{2} \underset{}{=} \frac{{|G_{x y} (f)|}^{2}}{G_{x x} (f) G_{y y} (f)} \leq 1 .

Transfer function (gain factor):

11

H (i f) = \frac{G_{x y} (f)}{G_{x x} (f)} .

The case studies evaluating tool for measurements SIGVIEW use these basic mathematical principles, but integral equations are transformed to discrete signal formulation.

4. Results and discussions

4.1. Case study Nr. 1 – upper gate building

The first investigative building is Upper gate located in the Modra city, in the west of Slovakia. Originally, this building was part of the old fortification of the city. It was built in 1610-1646. Building has rectangular floor plan and build-up area is 135 m². The building has three floors. The main building material was used stone in combination with mortar. The ceilings are wooden framed from a beam. The thickness of the walls is variable in the range from 705 to 1530 mm [8].

Fig. 2The view on upper gate building, numerical model and position of monitored points

a)

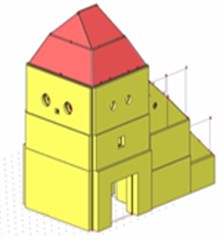
b)

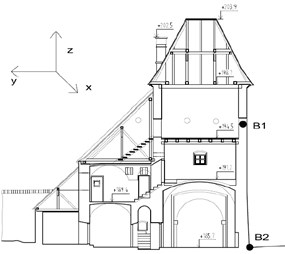
c)

Table 1Results of numerical and experimental analyses case study Nr. 1

	Results of numerical analyses	Results of experimental measurements	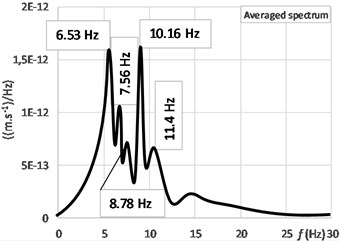Frequency response spectra
Natural frequency Nr. 1 [Hz]	6.46	6.53
Natural frequency Nr. 2 [Hz]	7.11	7.56
Natural frequency Nr. 1 [Hz]	8.48	8.78
Natural frequency Nr. 1 [Hz]	10.76	10.16
Natural frequency Nr. 1 [Hz]	12.9	11.40
RMS of the space vector of vibration velocity [mm/s]	0.69		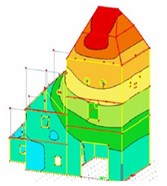Natural mode Nr. 1	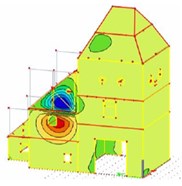Nm – local vibration

4.2. Case study Nr. 2 – King Stephan Parish church

The second investigative building is Tower of King Stephan Parish Church also located in the west of Slovakia, in Modra City. Originally, this tower was a separate object, and later, a church was attached to it. Tower was built in beginning of the 19 century and church was built in 1873-1876. The height of the main tower is 65.025 m and church have a height 23.75 m. The building is built from stone and their combination with mortar. On the lower floors there are stone ceilings in combination with mortar, and on the upper floors there are beamed and made of wood. The thickness of the walls is variable in the range from 820 to 1845 mm [9].

Fig. 3King Stephan Parish church view, numerical model and position of monitored points

a)

b)

Table 2Results of numerical and experimental analyses case study Nr. 2

	Results of numerical analyses	Results of experimental measurements	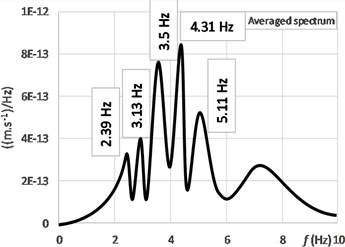Frequency response spectra
Natural frequency Nr. 1 [Hz]	2.73	2
Natural frequency Nr. 2 [Hz]	3.14	2.39
Natural frequency Nr. 1 [Hz]	3.93	3.13
Natural frequency Nr. 1 [Hz]	4.85	3.50
Natural frequency Nr. 1 [Hz]	5.29	4.31
RMS of the space vector of vibration velocity [mm/s]	0.58		Natural mode Nr. 1	Nm – local vibration

4.3. Case study Nr. 3 – Budatín castle

The third investigative building is Budatín castle. This castle is located in the northern part of Slovakia, in the city part of Budatín, belonging to the city of Žilina. Originally, it was a guard tower, the living quarters were added to it later. Tower was built in the end of 12th century. The tower has seven floors. The height of the main tower is 20 meters and its diameter is 12 meters. The building is built from stone and their combination with mortar. The ceilings are made from stone combination with mortar, and roof is beamed from wood. The thickness of the walls is variable in the range from 700 to 1500 mm [10].

Fig. 4Budatín castle view and position of monitored points

a)

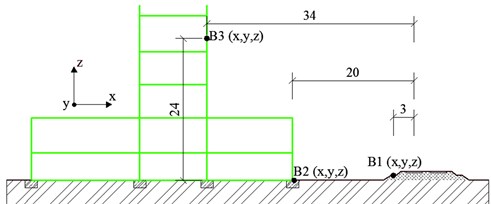
b)

Table 3Results of numerical and experimental analyses case study Nr. 3

	Results of numerical analyses	Results of experimental measurements	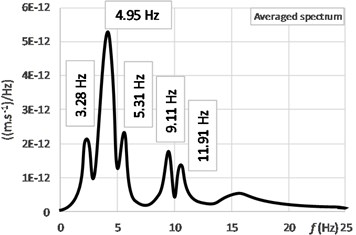Frequency response spectra
Natural frequency Nr. 1 [Hz]	2.73	3.82
Natural frequency Nr. 2 [Hz]	3.14	4.95
Natural frequency Nr. 1 [Hz]	3.93	5.31
Natural frequency Nr. 1 [Hz]	4.85	9.11
Natural frequency Nr. 1 [Hz]	5.29	11.91
RMS of the space vector of vibration velocity [mm/s]	2.580		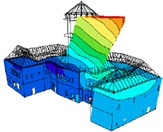Natural mode Nr. 1	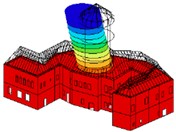Nm – local vibration

5. Conclusions

Dynamic parameters received via theoretical and experimental analysis from all three case studies are relevant. The results comparison in the frequency range indicates relatively good accordance. For each monumental building, the most important frequency broadband is defined. The frequency band is 1-15 Hz and it is low frequency effect of traffic induced seismicity. Using of these historical buildings FEM models is available for further static and dynamic analysis. Small differences between natural frequencies of the FEM models and the experimental dominant frequencies are caused by small differences of the material dynamic parameters. All amplitude RMS vibration velocities obtained in experimental measurements are too low to pass limits of structural stability and capacity. Any of results in the case studies do not indicate uncomfortable vibrations according limits of vibration human impact and quality of living. All the results presented in this publication complement knowledge in the field of transport induced seismicity. The database of sensitive historical buildings and the traffic seismicity effects is expanding nowadays. The most endangered buildings near traffic loaded roads and railways are designed to monitoring of traffic vibrations [11-13]. The measurements were based on the published results in scientific and research publications. The individual contribution of the article is verification of the knowledge of research teams from around the world [14-16]. The case studies presented in the paper highlight the importance of monitoring such structures in the context of the effects of technical seismicity even though they are not endangered.

References

François S., Pyl L., Masoumi H. R., Degrande G. The influence of dynamic soil-structure interaction on traffic induced vibrations in buildings. Soil Dynamics and Earthquake Engineering, Vol. 27, Issue 7, 2007, p. 655-674.

Publisher
KAláb Z., Lednická M., Kořínek R., Hrubešová E. Influence of local geological pattern on values of vibrations induced by road traffic. Acta Geophysica, Vol. 60, Issue 2, 2012, p. 426-437.

Publisher
Li G.-Q., Wang Z.-L., Chen S., Xu Y.-L. Field measurements and analyses of environmental vibrations induced by high-speed Maglev. Science of the Total Environment, Vol. 568, Issue 15, 2016, p. 1295-1307.

Publisher
Learning manual – Dynamics. Scia Group, http://nemetschek-scia.com/sk/software/product-selection/scia-engineer, 2017.

Search CrossRef
SignalLab e.K. Manual. Sigview, http://sigview.com/help/, 2017.

Search CrossRef
Valašková V., Papánová Z., Papán D. Modelling of technical seismicity effects from transport. Procedia earth and Planetary Science, World Multidisciplinary Earth Sciences Symposium WMESS Proceedings, 2015, p. 199-204.

Publisher
Valašková V., Papán D., Fričová J. Theoretical analysis of traffic seizmicity effect on important historical building in Modra town. Procedia Earth and Planetary Science, World Multidisciplinary Earth Sciences Symposium WMESS Proceedings, 2015, p. 193-198.

Publisher
Kantek K. Modra, City Full of History, Guide to History and Monuments. City of Modra, 1997.

Search CrossRef
Lehotska A. Hystory of Modra. Slovak Academy of Science, 1961.

Search CrossRef
Mládenej J. Project Documentation of Budatín Castle. Technical Administration of the Castle, 2006.

Search CrossRef
Kowalska-Koczwara A., Stypula K. Assessment of the vibration influence on humans in buildings in the standards of different countries. Procedia Engineering, Vol. 161, 2016, p. 970-974.

Publisher
Figuli L., Bedon Ch., Zvaková Z., Jangl Š., Kavický V. Dynamic analysis of a blast loaded steel structure. Procedia Engineering, Vol. 199, 2017, p. 2463-2470.

Publisher
Latifi R., Razani R. Retraction: Seismic performance of tuned mass damper on Shazand Railway Bridge induced by train. Journal of Measurements in Engineering, Vol. 6, Issue 2, 2018, p. 126-126.

Publisher
Lu J., Wang Y., Chen J. Detection of tectonically deformed coal using model-based joint inversion of multi-component seismic data, ENERGIES, Vol. 11, Issue 4, 2018, p. 829.

Publisher
Real J. I., Zamorano C., Hernández C., Comendador R., Real T. Computational considerations of 3-D finite element method models of railway vibration prediction in ballasted tracks. Journal of Vibroengineering, Vol. 16, Issue 4, 2014, p. 1709-1722.

Search CrossRef
Xu Y. L., Yu Z.-F., Zhan S. Experimental study of a hybrid platform for high-tech equipment protection against earthquake and microvibration. Earthquake Engineering and Structural Dynamics, Vol. 37, Issues 5-25, 2008, p. 747-767.

Publisher

Cited by

Vibration monitoring of structures in the light of the Polish and international requirements

Aneta Herbut | Anna Jakubczyk-Gałczyńska | Marek Wyjadłowski

(2023)

Seismic Protection of RC Buildings by Polymeric Infill Wall-Frame Interface

Ahmet Tugrul Akyildiz | Alicja Kowalska-Koczwara | Łukasz Hojdys

(2021)

The importance of the „0”state in the context of dynamic influences

(2019)

About this article

Received

28 November 2018

Accepted

28 December 2018

Published

31 December 2018

DOI

https://doi.org/10.21595/jme.2018.20413

Keywords

traffic seismicity

vibrations

experimental results

numerical analysis

Acknowledgements

This paper was supported by the Grant National Agency VEGA of the Slovak Republic (Grant No. 1/0005/16).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 03 31

Mitigation of train-induced vibrations on nearby high-rise buildings by open or geofoam-filled trenches

Denise-Penelope N. Kontoni, Ahmed Abdelraheem Farghaly

Research article

2018 06 30

Numerical analysis on longitudinal seismic responses of high-speed railway bridges isolated by friction pendulum bearings

Zhiwu Yu, Haiyan Li, Biao Wei, Lizhong Jiang, Jianfeng Mao

Research article

2017 09 26

Vibration induced by railway traffic-zones of influence on buildings and humans

Filip Pachla, Bartosz Radecki Pawlik, Krzysztof Stypuła, Tadeusz Tatara

Research article

2017 08 15

Numerical analysis on dynamic responses of single-storey buildings under seismic effects

Feng Hui Dong, Can Hong Lou, Yuan Liu, Bao Jiang Sun

V. Valašková, D. Papán, and Z. Papánová, “Traffic seismicity effect on monumental buildings – results of case studies,” Journal of Measurements in Engineering, Vol. 6, No. 4, pp. 210–217, Dec. 2018, https://doi.org/10.21595/jme.2018.20413

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jme.2018.20413
UR  - https://doi.org/10.21595/jme.2018.20413
TI  - Traffic seismicity effect on monumental buildings – results of case studies
T2  - Journal of Measurements in Engineering
AU  - Valašková, Veronika
AU  - Papán, Daniel
AU  - Papánová, Zuzana
PY  - 2018
DA  - 2018/12/31
PB  - JVE International Ltd.
SP  - 210-217
IS  - 4
VL  - 6
SN  - 2335-2124
SN  - 2424-4635
ER  - 

Copy Ris

Copied to clipboard!

@article{Vala_kov__2018,
	doi = {10.21595/jme.2018.20413},
	url = {https://doi.org/10.21595/jme.2018.20413},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {6},
	number = {4},
	pages = {210--217},
	author = {Veronika Vala{\v{s}}kov{\'{a}} and Daniel Pap{\'{a}}n and Zuzana Pap{\'{a}}nov{\'{a}}},
	title = {Traffic seismicity effect on monumental buildings {\textendash} results of case studies},
	journal = {Journal of Measurements in Engineering}
}

Copy Bibtex

Copied to clipboard!

[1]V. Valašková, D. Papán, and Z. Papánová, “Traffic seismicity effect on monumental buildings – results of case studies,” Journal of Measurements in Engineering, vol. 6, no. 4, pp. 210–217, Dec. 2018, doi: 10.21595/jme.2018.20413.

Copy IEEE

Copied to clipboard!

Valašková, Veronika, Daniel Papán, and Zuzana Papánová. “Traffic Seismicity Effect on Monumental Buildings – Results of Case Studies.” Journal of Measurements in Engineering 6, no. 4 (December 31, 2018): 210–17. https://doi.org/10.21595/jme.2018.20413.

Copy Chicago

Copied to clipboard!

Traffic seismicity effect on monumental buildings – results of case studies

Abstract

1. Introduction

2. The FEM frequency analysis of the monumental building

2.1. The solving of dynamic problems in FEM

3. The experimental analysis in frequency domain

3.1. Spectral functions – basic principles

4. Results and discussions

4.1. Case study Nr. 1 – upper gate building

4.2. Case study Nr. 2 – King Stephan Parish church

4.3. Case study Nr. 3 – Budatín castle

5. Conclusions

References

Cited by

About this article

Related Articles