Abstract
The aim of the work is to eliminate the shortcomings of the existing methods of selecting the parameters of grapple for bulk materials and to develop an appropriate software. The necessary analytical dependences for the existing graphic data were obtained, which allow to choose the optimal parameters of the grapple with the help of a computer. The recommendations on the choice of parameters of the grapple depending on the load capacity of the grab crane and bulk material types are given, according to the results of the research.
1. Introduction
Grab cranes are widely used in the handling of bulk cargoes in transport, industry and construction. The performance and cost of loading and unloading operations depend on the quality of grapples and the degree of their specialization in relation to different operating conditions and properties of goods. The grapple quality criterion is the ratio of its mass to the crane load capacity, so the optimal choice task is to reduce the mass fraction of the grapple and to increase the share of payload within the crane load capacity [1-3]. The solution of this problem is possible by calculating the parameters of the grapple with the help of a computer. It must be noted that in the existing works on this subject [4-8] this task hasn’t been set at all.
The calculation of a two-jaw rope grapple with long links can be performed with the help of methods [2]. To calculate the required own weight of the grapple, variable coefficients which characterize the geometric parameters of the process of scooping the material with the grapple are used. These coefficients are given by integral dependences, the calculation of which is complicated by the use of a significant amount of additional data, and the values are represented by graphs, and each coefficient is a function depending on the generalized value and the reduced multiplicity of the polispast , that is , , 1, 2, 3, 3, 4, 5 (indexing is stored in accordance with [2]). While developing the application program for computers this form of representation of the above coefficients turned out to be unacceptable, because to find them according to the integral dependencies is rather difficult due to the fact that not all the original data are defined, and the choice of coefficients on the graphs reduces the calculation accuracy and leads to the interruption of the program, which is undesirable.
2. Analytical dependences for calculating the parameters of the grapple
Based on the method of three points and approximating algorithms described in the pointed works [9, 10], the following dependencies for dimensionless coefficients , , , , , were obtained , which are necessary for the calculation of the grapple parameters:
The software module (Determination of Coefficients) was developed in Compaq Visual Fortran environment. The module allows to obtain the values of the desired coefficients depending on and , and if it is necessary – graphs according to the found analytical equations , (1-6). Fig. 1 shows a graph to define in semi-log coordinates. The comparison of the obtained values of the coefficients with the corresponding ones from [2] showed that the relative errors at large values are rather small and they increase with a decrease , but do not exceed10 %.
3. The determination of the grapple mass
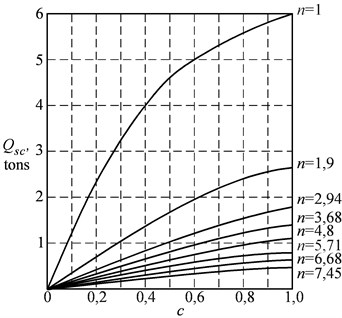
To study the dependence of the grapple mass on generalized value , the reduced multiplicity of the polispast , crane capacity, the size of the reloaded piece of material and its state, the special software modules (The Determination of the Grapple Mass) and (The Calculation of the Grapple for a Given Crane Capacity) were developed. The values of the grapple mass , depending on the generalized value and reduced multiplicity of the polyspast were obtained, as well as the graphic picture of these dependencies. An example of the calculation result is shown at Fig. 2. The researches which were carried out allow to make the conclusion that the best values of the grapple mass can be achieved at the multiplicity of the closing rope polispast 2, …, 6. At the kinematic multiplicity of the polispast 1 there is a significant increase in the mass of the grapple, at 7, …, 8 the value of the grapple mass decreases slightly, i.e. it is impractical to use the polispast of greater multiplicity due to the complexity of the design.
Fig. 1The dependence of the coefficient A5 on the generalized value c and the reduced multiplicity of the polispast n
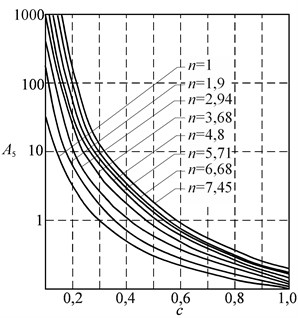
Fig. 2The dependence of the grapple mass Qsc on the generalized value c and the reduced multiplicity of the polispast n
The studies show that the nature of the change in the grapple mass from its generalized value and the reduced multiplicity of the polispast does not depend significantly on the crane capacity, the size of the transported piece and the state of the material for different loads. So, Table 1 shows the values of the grapple mass depending on the state of the material (pyrites ordinary) for cranes with a lifting capacity of 10 tons.
4. The determining of the grapple capacity
A software module (The Determination of the Grapple Capacity) was developed, according to the known values of physical and mechanical properties of bulk materials and their three states, and taking into account the crane capacity of 2, 5, 10, 20 and 32 tons. The results of the calculations allowed to construct graphs of the dependencies of the grapple capacity on the bulk density of the material. The curves are identical in their characteristics, but it should be taken into account that the required scooping capacity is provided by changes in the multiplicity of the polispast. When the material is freshly poured the preferred multiplicity of the polispast is 3, …, 4, when it is incompacted, 4, …, 5, and when it is compacted, 5, …, 6. At Fig. 3 a graph of the dependencies of the grapple capacity on the bulk density of the material is presented, where 1 is the curve for freshly poured material, 2 – the curve for loose (incompacted) material, 3 – the curve for compacted material; I, II, III, IV, V, VI – groups of materials according to their state [2].
Table 1Grapple mass and the multiplicity of the polyspast depending on the condition of the material being overloaded
The state of the material | Grapple mass, kg | Multiplicity of the polyspast | |
min | max | ||
Freshly poured | 3716 | 4178 | 3/4 |
Incompacted | 3841 | 4339 | 4/5 |
Compacted | 3974 | 4427 | 5/6 |
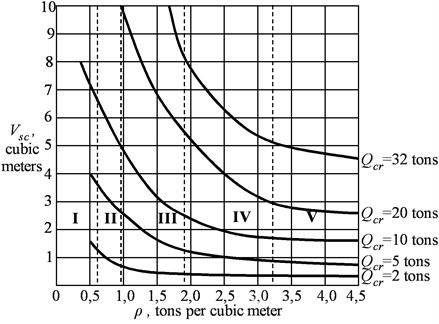
Since the nature of the curves is identical for the three states of the material with a slight spread of values (up to 10 %), the represented family of graphs can be replaced by one averaged curve – 4. After replacing the graphs by the averaged curve, a general graph of the dependence of the grapple capacity on the bulk density and the crane capacity was constructed – Fig. 4. Analytical dependencies were obtained for each of these curves according to the crane capacity .
Fig. 3The dependence of the grapple capacity on the bulk density of the material
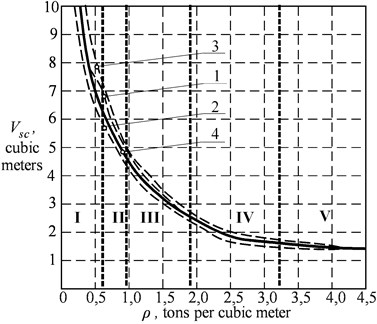
Fig. 4The dependence of the grapple capacity on bulk density of material and loading capacity of the crane
The previously mentioned methods [9, 10] were used to determine the dependencies. The analytical dependencies on the bulk density of the material are determined.
The capacity of the crane 2 tons:
The capacity of the crane 5 tons:
The capacity of the crane 10 tons:
The capacity of the crane 20 tons:
The capacity of the crane 32 tons:
The general two-parameters equation was obtained :
The obtained results allow to determine the capacity of the grapple on the basis of the bulk density of the material and its state. So for the crane with a capacity of 10 tons, the grapple capacity for materials I, II, III groups can be selected by the average value of the capacity for each of the groups, i.e. it is 7 m3, 5 m3 and 3 m3, respectively, for materials of IV, V and VI groups, a grapple with a capacity of 2 m3 can be used – Fig. 5. According to this nomogram, it is possible to choose the optimal grapple capacity for the given parameters in operating conditions. In Table 2 the optimal values of the grapple capacity in m3 for cranes with lifting capacity of 2, 5, 10, 20 and 32 tons for five groups of material states are given.
Fig. 5The nomogram to determine the capacity of the grapple depending on the load capacity of the crane and the group of reloaded material
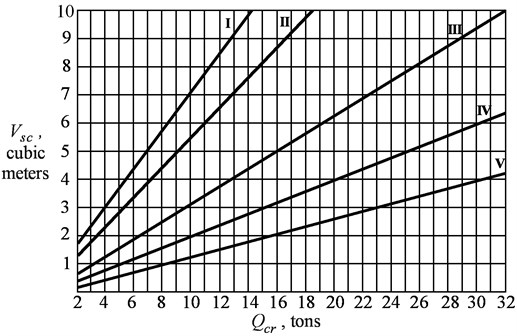
Table 2The optimal capacity of the grapple according to the crane capacity and a group of materials
The capacity of the crane , tons | Groups of a material state | ||||
I | II | III | IV | V | |
2 | 1,5 | 1,2 | 0,8 | 0,5 | 0,3 |
5 | 3,5 | 2,8 | 1,7 | 1,0 | 0,5 |
10 | 7,0 | 5,5 | 3,2 | 2,0 | 1,2 |
20 | – | – | 6,5 | 4,0 | 2,8 |
32 | – | – | 10,0 | 6,2 | 4,3 |
5. Conclusions
The practical value and novelty of the work are as follows.
Analytical dependencies for dimensionless coefficients allowing to determine the grapple mass, as well as to find the capacity of the grapple are obtained.
The area of the designing and selection of grapples is expanded, because dimensionless coefficients can be found at any value of the generalized value and the reduced multiplicity of the polispast.
The methods of designing and selection of grapples for different groups of materials and any load capacity of grab cranes has been developed and implemented. The correctness of the results is confirmed by test calculations.
The studies revealed, that the optimal value of the mass of the grapple is achieved when the values of the multiplicity of pulley end of the rope 2-6, at the same time, the mass of the grapple is not significantly affected by the crane capacity, the size of the overloaded piece and the state of the material.
References
-
The Calculations of Crane Mechanisms and Their Parts. Vniiptmash, Moscow, 1993, p. 187, (in Russian).
-
Tauber B. Grab Mechanisms. Mechanical Engineering, Moscow, 1985, p. 272, (in Russian).
-
Guidance Document RD 31.46.07 – 87. Rope Grabs for Bulk Cargo. Typical Strength Calculations. Methods. Mortechinformreklama, Moscow, 1987, p. 142, (in Russian).
-
Abramovich I. Features of calculation of grab mechanisms of cranes. Lifting and Transport Mechanisms, Vol. 3, 2007, p. 2-4, (in Russian).
-
Scheffler M. Grundlagen der Fordretechnik – Element und Triebwerke. Braunschweig, 1994, p. 340.
-
Sjoberg J., Lindkvist S., Linder J., Ohr J. Interactive multiobjective optimization for a grab-shift unloader crane. Proceedings of the 19th World Congress the International Federation of Automatic Control, South Africa, Cape Town, 2014.
-
Mikhailov I. V. The Method of Strength Calculation of Rope Grabs When Scooping Bulk Cargo. Ph.D. Thesis, Novocherkassk, 2010, p. 24, (in Russian).
-
Filatov A., Slavin B., Mikhailov I. The Influence of the Fractional Composition of the Load at the Scooping Ability of the Grab. Problems of Dynamics and Strength of Actuators and Machines, Astrakhan State Technical University, 2004, p. 79, (in Russian).
-
Tukey J. Exploratory Data Analysis. Addison Wesley Publishing Company, 1977, p. 711.
-
Kotelnikov R. B. The Analysis of the Results of Observations. Energoizdat, Moscow, 1986, p. 144, (in Russian).
