The symmetrical cell eigenfrequency method for periodic structure stop-band definition

1. Introduction

The classical Floquet theory is developed in numerous papers, starting from classical book by L. Brillouin [1] and papers by D. Mead [2] to the contemporary research [3]. However, the classical theory has several drawbacks. One of them is the inapplicability to the non-linear cases.

Works within the non-linear periodic structures mostly analyze the energy flow using WFEM (wave finite element method) [4]. In some papers, authors attempted to use Floquet theory in the non-linear case [5]. However, the general approach remains questionable. The boundary problem may be formulated for the finite counterpart of the infinite periodic waveguide. Thus, it is useful to find the connection between the infinite periodic waveguide and its finite counterpart.

It turns out that the symmetrical periodicity cell with symmetrical boundary conditions allow one to find the stop-band boundaries without analyzing the infinite structure. In the paper, several applications of the unit symmetrical cell are shown. While it is working as the exact method in the linear cases, in the non-linear cases it could be considered as the stop-band equation approximation.

The paper contains three infinite periodic structure problems. In Section 2 the classical Floquet theory application is considered. The axial rod vibration case is a typical linear equation and Floquet theory may be used to analyze the infinite periodic structure. The unit symmetrical cell, in this case, gives the exact stop-band boundaries positions. Section 3 is dedicated to the infinite periodic membrane case. In this case, the modified Floquet theory may be used. On contrary, the unit symmetrical cell eigenfrequencies may be used without any additional assumptions. Section 4 describes the non-linear interface case, which requires additional techniques to obtain the symmetrical unit cell backbone curve.

2. Floquet theory for the axial rod vibration case

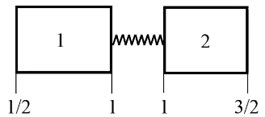
Within the paper, we consider the one-dimensional periodic structures. The structure is meant to have two different components that have different waveguide properties. The typical periodic structure is shown in Fig. 1.

It is assumed, that each part in the Fig. 1 has its own parameters such as length $l_1$ and dilatation wave sound velocity $c_1=\sqrt{E_1/{\rho }_1}$. We use the Floquet theorem to analyze the infinite periodic structure spectra. Let us consider the infinite periodic axial rod vibration problem. We assume that $i$th part of the periodic structure with displacement $u_i(x,t)$ has the governing equation:

We consider a time-harmonic state $u\left(x,t\right)=u\left(x\right)\exp (-i\omega t)$. Therefore, below the time-dependence is omitted. With time-dependence introduced we use following dimensionless parameters $\mathrm{\Omega }=\omega l_1/c_1$, $\gamma =l_2/l_1$.

Fig. 1A schematic diagram of a periodic structure

To solve the spectral problem of the infinite periodic structure two types of conditions are required. The interfacial conditions represent the mass and force balance in the periodic structure. For the axial rod vibration case, they have a form Eq. (2):

To complete the spectral problem solution one has to introduce the periodicity conditions. They are provided by the Floquet theorem and have the form:

In Eq. (3) $\mathrm{\Lambda }\left(\mathrm{\Omega }\right)$ is the periodicity parameter, which depends only on the non-dimensional frequency parameter. We will refer to it below as the Floquet parameter.

When solution in a form $u_i\left(x\right)=b_{i,1}\exp \left(i\mathrm{\Omega }x\right)+b_{i,2}\exp (-i\mathrm{\Omega }x)$ is substituted into the system Eqs. (2)-(3), we obtain the homogenous system of the algebraic equations with respect to the unknown displacements $b_{i,j}$. The determinant of the system defines the spectra, which is in this case the second-order polynomial in $\mathrm{\Lambda }\left(\mathrm{\Omega }\right)$. For each frequency $\mathrm{\Omega }$, the polynomial has two roots which are schematically shown in Fig. 2.

Fig. 2The roots Λ(Ω) of the system Eqs. (2)-(3) determinant

In the zones with property $abs\left(\mathrm{\Lambda }\mathrm{}\right)>\text{1}$, the wave propagation is blocked by the interference, following Bloch’s notation they are called stop-bands. Vice versa, in the zones with property $abs\left(\mathrm{\Lambda }\right)=$ 1 waves are propagating freely, these zones are pass-bands.

In the paper [6] is proven that eigenfrequencies of a unit symmetrical periodicity cell with symmetrical boundary conditions are exactly placed on stop-band boundaries. The symmetrical unit cell is the structure that schematically can be shown as in Fig. 3.

For finite counterpart, the periodicity conditions are replaced with the boundary conditions. The interfacial conditions have the same form. The symmetrical boundary conditions for symmetrical periodicity cell eigenfrequency problem in case of the axial rod vibration have the form:

Fig. 3The symmetrical periodicity cell

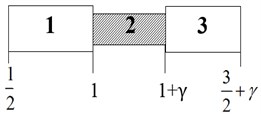
The symmetrical boundary conditions more strict formulation for more complex cases. In [3]. the symmetrical boundary conditions are defined with bi-orthogonality conditions for reduced elastic layer theories.

The eigenfrequencies of a symmetrical periodicity cell are placed on stop-band boundaries as in Fig. 4. In the Fig. 4 the eigenfrequencies for graphical matters are placed on a line$abs\left(\mathrm{\Lambda }\right)=$ 1.

Fig. 4Eigenfrequencies of the systems Eqs. (2), (4) and (2), (5) (different colors) compared with the roots Λ(Ω) of the system Eqs. (2)-(3) determinant

In a linear case, the spectra of the infinite periodic structure and the finite symmetrical unit cell are exactly the dual problems. We can find the stop-band boundaries and thus define them in two ways. The eigenfrequencies problem is less computationally intensive, so it allows one to find the stop-band boundaries more quickly.

3. Floquet theory for the radially-periodic membrane vibration case

In the polar coordinates, the Floquet theory cannot be formulated in the classical form Eqs. (3). Let us consider the simple problem of the periodic membrane vibration case. The example of the radially periodic membrane is shown in Fig. 5.

Fig. 5The radially periodic membrane

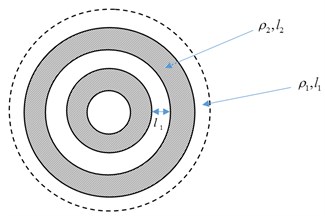
The radially periodic membrane problem is close to the axial rod vibration problem. The membrane vibration has the governing equation that is in limiting case $r\to \infty$ gives exactly the axial rod vibration problem. The governing equation for the radial membrane has the form:

However, we still can formulate the symmetrical cell eigenfrequency problem, which in this case schematically can be shown as in Fig. 6.

Fig. 6The symmetrical periodicity cell

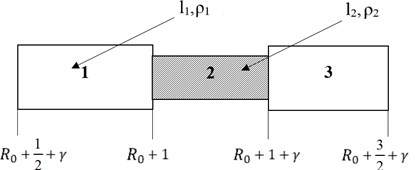
The specter of the symmetrical periodicity cell, in this case, is depend on how close to the polar coordinates origin unit cell is placed. Thus, it is expedient to introduce the polar coordinates parameter $R_0$ that shows how close to the polar coordinates origin we are.

With the general solution of the governing equation in form $u\left(r\right)=b_{i,1}{J}_m\left(r\right)+b_{i,2}{Y}_m\left(r\right)$. With $J_m\left(r\right)$, $Y_m\left(r\right)$ Bessel functions of first and second kind of integer order $m$ are designated. With the symmetrical boundary conditions Eqs. (4)-(5), we can obtain the eigenfrequency equation, which gives the stop-band boundaries at the limiting case $R_0\to \infty$ as it is shown in Fig. 7.

Fig. 7Eigenfrequencies (in polar coordinates for R0= 0, 0.1, …, 1) of the systems Eqs. (2), (4) and (2), (5) (different colors) compared with the roots Λ(Ω) of the system Eqs. (2)-(3) determinant

In Fig. 7 is seen that in the periodic membrane case, the stop-band position depends on polar origin proximity. For the polar coordinates case, we can formulate Floquet theory as it is done in [7]. Instead of the Floquet polynomial, we can obtain a differential equation that defines stop-bands. Nevertheless, it is out of the scope of the paper. However, we note that the eigenfrequencies of a unit periodicity cell agree with Floquet theory.

Thus, one can obtain the stop-band boundaries prediction with the symmetrical eigenfrequency problem. The symmetrical unit periodicity cell eigenfrequency does not require specific Floquet theory extension and can be considered as a dual problem to a Floquet theory spectral problem for the infinite periodic membrane. We emphasize that the eigenfrequency problem does not require to formulate any additional theory assumptions.

4. Symmetrical unit cell eigenfrequencies for a unit weakly non-linear periodicity cell case

The periodic membrane case in the polar coordinated can also be considered as a non-linear case. The linearity property is broken in the translational symmetry part. This property is essential for Floquet theory formulation. The more common, but rather still weak non-linearity can be achieved with non-linear stiffness spring interface. This can be schematically illustrated as in Fig. 8.

The waveguides have an arbitrary governing equation. For simplicity, let us consider the axial rod vibration Eq. (1), i.e. the case considered in Section 2. The non-linear interface conditions can be written as Eq. (7):

Fig. 8The symmetrical periodicity cell

In Eq. (7) we refer to $\kappa$ as the linear stiffness and $N$ as the non-linear stiffness. We use the same symmetrical boundary conditions Eqs. (4)-(5) as in the previous cases and the axial rod vibration case common solution in a form $u_i\left(x,t\right)={(b}_{i,1}\exp \left(i\mathrm{\Omega }x\right)+b_{i,2}\exp (-i\mathrm{\Omega }x))*\cos \left(\omega t\right)$. We can rewrite the system Eqs. (7), (4)-(5) in the form Eq. (8):

The non-linear interfacial conditions do not allow to cancel the time dependency. To cancel the time dependency out, we use the harmonic balance method and write the time-dependent part as ${\cos }^3\omega t=\frac{3}{4}\cos \left(\omega t\right)+\frac{1}{4}\cos \left(3\omega t\right)$. Term $\cos \left(3\omega t\right)$ is omitted and the resulting system with the time-dependance cancelled out is written as:

The system Eq. (9) has the cubic equation with respect to the unknown displacements $b_{i,j}$. Therefore, we cannot find the usual determinant for the system Eq. (9). We use the resultants method [8] to obtain the symmetrical cell backbone equation that shows how the eigenfrequencies depend on a non-linearity parameter $\beta =b_{\mathrm{1,1}}^{2}N$ (the displacement may be chosen arbitrary). The solution of the backbone equation has the form shown in Fig. 9.

Fig. 9Eigenfrequencies (for non-linear interface) of the systems Eqs. (7), (4) and (7), (5) (different colors)

We note that the eigenfrequencies give the same result for $\beta =$ 0 as the determinant in non-linear interfacial conditions with non-linear stiffness $N$ set to zero.

The Fig. 9 may be considered as the stop-band position approximation for the non-linear case. However, the Floquet theory extension formulation is required in order to check the correspondence between the exact stop-band position and the unit symmetrical periodicity cell eigenfrequencies.

5. Conclusions

In the paper, we describe the unit symmetrical cell method for the stop-band location position. This method in contrast with the existing method like Floquet theorem in the linear case and the WFEM method at one hand does not require the additional assumptions (like the linearity of the problem) and at the other hand require intensive computations.

In the linear case, the unit symmetrical cell eigenfrequencies with the symmetrical boundary conditions exactly define the stop-band positions. Thus, it is an exactly dual problem to the classical Floquet theory spectra for the infinite periodic structure in the linear case.

In the non-linear case, however, the exact position of the stop-bands is a discussion topic. However, the unit symmetrical cell eigenfrequencies may be at least an approximation to the stop-band boundaries equation. The method does not require any additional assumptions and may be implemented for any type of the non-linear structures from problems in the polar coordinates to the non-linear stiffness interface.