Abstract
The stiffness of boundary conditions in mechanical structures is difficult to represent. A method is proposed to model the mechanical performance of the clamped boundary condition based on thin-layer element. Firstly, the contact surface of clamped boundary condition is parameterized by using isotropic thin-layer element to model the normal and tangential contact stiffness. Secondly, material parameter of thin-layer element is identified by using experimental modal data, parameter identification is transformed as an optimization problem. Experimental investigation is undertaken to verify the proposed method by employing an aluminum honeycomb panel, the numerical model of which is constructed by using the equivalent theory. Thin-layer elements with different properties are used to simulate the mechanical properties in different area of the boundary conditions, and the experimental modal data is adopted to identify the material parameters. Results show that the width to thickness ratio of the thin layer element has a great influence on the identification results.
Highlights
- Stiffness of the boundary condition is characterized by using thin-layer element.
- Material parameter of thin-layer element is identified by using experimental modal data.
- The width to thickness ratio of the thin layer element has great influences.
1. Introduction
Investigations on modeling of boundary conditions have attracted interests of researchers [1, 2]. To determine the stiffness of clamped boundary conditions, contact models [3, 4] can reflect the contact mechanism through analysis the asperities behavior. In order to obtain the quantitative nonlinear stiffness, identification of nonlinearities is always adopted [5]. However, the contact analysis for boundary conditions will be time consuming when apply to modeling of complex structures.
Identification of the boundary conditions from experimental data is an effective solution to improve the modeling accuracy. Pabst and Hagedorn [6] proposed an inverse method to identify the boundary stiffness and damping parameters of a visco-elastically clamped beam by using modal data. Yang et al. [7] constructed a numerical model to solve multi-variables inverse problems for a beam with elastic boundary support. Wang [8] extended the cross-model cross-mode method for model updating by incorporating the connection flexibility and boundary conditions. Yang et al. [9] proposed an approach using frequency response functions to identify the joint parameters including the rotational stiffness. Baruh and Boka [10] modeled boundary conditions using axial and torsional springs. Boundary stiffness are simplified as spring models in the above researches, modeling difficulties will arise when apply spring models to complex structures, because spring element should be allocated in each boundary constraints, and the deficiency is obvious for modeling large contact surface.
Parameterization plays an important role in the stiffness identification of boundary conditions [11, 12]. Mottershead et al. [13] indicated that parameterization is critical in updating of boundary conditions, the boundary stiffness in a cantilever was modeled as the effective length of elements closest to the joint. The above approximate stiffness characterization methods are the alternative parametrized models of boundary stiffness, and modeling complexities still exist. In order to solve this problem, thin-layer element has been introduced to model the dynamics of mechanical joints [14-16], The concept of thin-layer element was first proposed by Desai [17] who applied to the contact analysis in geotechnical engineering, and has been widely applied in equivalent modeling of joints, The normal and tangential stiffness of the contact surface can be accurately described by the thin-layer elements [18].
Based on the basic theory of thin-layer element, this paper parameterized the contact surface of the clamped boundary. The elastic parameters of the thin-layer element are identified by using the experimental modal data. Furthermore, the influence of the weighted matrix and the ratio coefficient of the thin-layer element are also investigated.
2. Basic theory
2.1. Thin-layer element
The size of thin-layer element is ××, according to the principle of virtual displacement derived the following equation:
and are the lengths of the thin-layer elements in the and directions in the local coordinate system, and is the -direction size. Stiffness matrix [] of thin-layer element is calculated by isoparametric transformation:
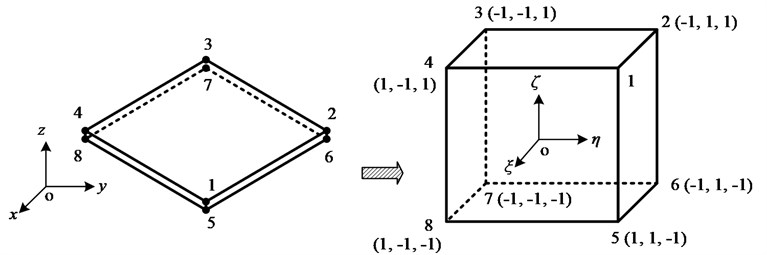
Fig. 1 shows the isoparametric transformation of thin-layer element. Where , , are natural coordinate symbols, [] is the Jacobi ratio matrix, and when the coordinates of the natural and local coordinates are consistent, which has the following form:
The following numerical expression for stiffness matrix [] of thin-layer element can be obtained by the calculation of two-node Gaussian integration method:
where , , and are the Gaussian integral weight function.
It is assumed that the thickness of the thin-layer element is much smaller than the feature sizes and . In this case, the in-plane strain components (, , ) and the stress components (, , ) of the element are ignored. Which leads to the strain component 0. Therefore, only three strain components at the Gaussian point of the thin-layer element are not zero. The strain component can be simplified to . According to the previous analysis, assuming that the normal and tangential contact properties of the interface are independent and the two tangential contact properties are consistent.
Fig. 1Isoparametric change of thin-layer element
In the finite element analysis, according to the basic theory of thin-layer element, the constitutive equation of the material will be transformed to the following form:
In this equation, the normal elastic constant and the tangent elastic constant are correlated. The selection of different thickness of thin layer element have a great influence on the calculation results. Desai et al. [17] recommended the width to thickness ratio for obtaining the exact result, the ratio is expressed as:
Calculating the contact stiffness is one of the key problems on thin-layer element for simulating the bolt connected structures. When the contact surface maintains a linear bonding state. The constitutive relation of the material can be integrated into the thin-layer element and the finite element dynamic analysis of the connection structure can be carried out. However, there are some shortcomings that need to be tested separately for the contact stiffness in different directions, and the requirements for the test device and the test method.
2.2. Parameter identification
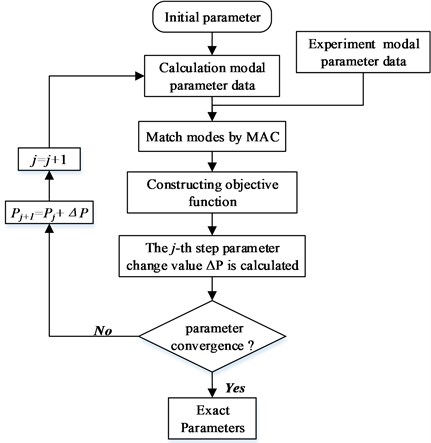
In this paper, material parameter identification of thin-layer elements is transformed as an optimization problem. The parameters to be identified are the elastic modulus and the shear modulus of the thin-layer element. And the minimum value of the objective function is expressed:
where is the discrepancy between the experimental data and the numerical results. is the weighted matrix, which reflects the relative weight of modal parameters. In general, the expression of is the identity matrix or . Until the numerical modal data satisfy the requirement of precision, the accurate contact surface material parameters are obtained. The procedure of the above optimization problem is shown in Fig. 2.
Fig. 2The flow chat of elastic parameters identification
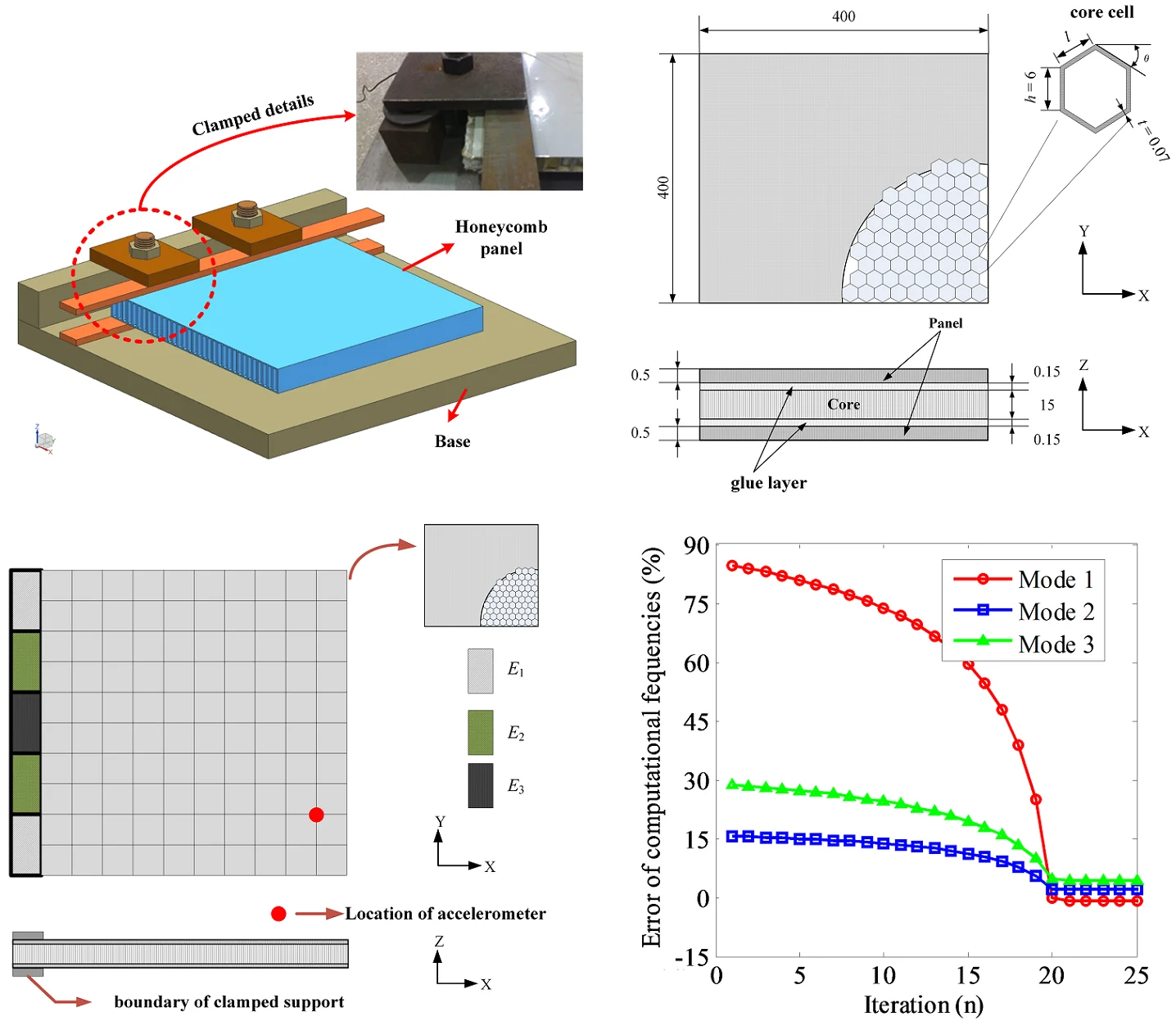
3. Case studies: a clamped honeycomb panel
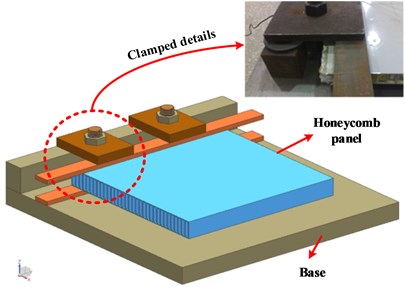
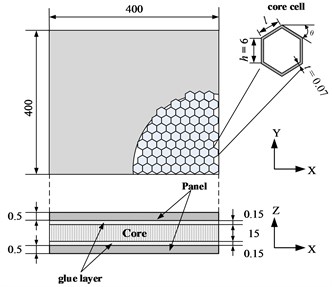
An aluminum honeycomb sandwich panel is clamped on the fixed stage is shown in Fig. 3. The contact surface is modeled by thin-layer elements of three different properties. The dimension of the honeycomb sandwich panel is 400 mm×400 mm×16.3 mm. Panel and core materials are aluminum, the elastic Modulus is 68 GPa and density is 2700 kg/m3.Adhesive material is epoxy resin which elastic Modulus is 5 GPa and density is 1500 kg/m3.
Fig. 3The clamped honeycomb panel
a)
b)
3.1. Equivalent modeling
Neglecting lateral shearing stress, the honeycomb core is equivalent to an orthotropic material of uniform thickness. As a result, the face sheets are modeled as the upper and the lower panels, the core is equivalent to a solid structure. The interlaminar shear effect caused by the weak layer has an important influence on the macroscopic mechanical properties of the sandwich material. Therefore, the influence of the adhesive layer on the dynamic characteristics of the honeycomb sandwich composite can’t be neglected. Fig. 4 shows the finite element model of honeycomb plate. Clamped boundary condition is modeled by isotropic thin-layer elements.
3.2. Parameter identification
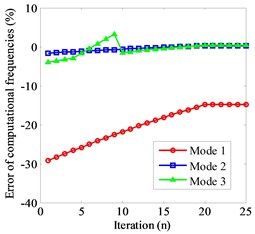
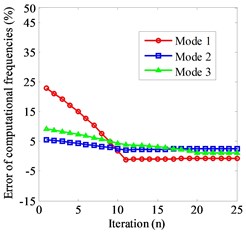
The influence of different weighting matrices on the results of parameter identification is studied by establishing a thin-layer element with 100. After the identification, the accuracy of the inherent frequency is greatly improved. The error of the first three order natural frequency is less than 2.63 %, the convergence error can be effectively reduced by .
Based on the above results, parameter identification are carried out when the of thin layer elements is 10, 50, 100, 500, respectively. The convergence error is reduced with the increase of the width and thickness ratio. However, the more iterations are needed for convergence. Table 2 is the comparison of calculation natural frequency and parameter identification results of thin-layer element under different .
In this case, the stiffness properties of the contact surface are determined by the elastic parameters and the thickness of the thin layer element.
Fig. 4Numerical model of the clamped honeycomb plate
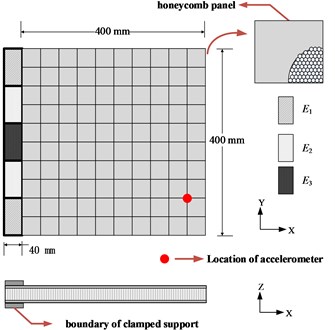
Fig. 5Frequency convergence under different R: a) R= 10, b) R= 50, c) R= 100, d) R= 500
a)
b)
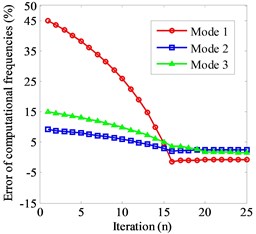
c)
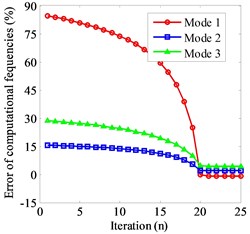
d)
Table 1Comparison of natural frequency
Mode | / Hz | Initial | |||
/ Hz | Error (%) | / Hz | Error (%) | ||
1 | 49.59 | 71.94 | 45.07 | 49.27 | –0.64 |
2 | 199.8 | 218.09 | 9.15 | 205.05 | 2.63 |
3 | 411.93 | 473.83 | 15.3 | 416.16 | 1.03 |
Table 2Comparisons of calculated frequency errors under different R
Mode | / Hz | 10 | 50 | 100 | 500 | ||||
/ Hz | Error (%) | / Hz | Error (%) | / Hz | Error (%) | / Hz | Error (%) | ||
1 | 49.59 | 42.53 | –14.23 | 49.30 | –0.56 | 49.27 | –0.64 | 49.32 | –0.54 |
2 | 199.8 | 200.53 | 0.36 | 205.10 | 2.65 | 205.05 | 2.63 | 205.14 | 2.67 |
3 | 411.93 | 414.37 | 0.59 | 414.70 | 0.68 | 416.16 | 1.03 | 414.47 | 0.62 |
4. Conclusions
An approach on identifying the stiffness of the clamped boundary condition is proposed in this paper. The contact surface is modeled based on the theory of thin-layer element, and modal parameters are used to identify the material parameters of thin-layer element. Three kinds of thin layer elements with different properties are used to simulate the mechanical change of the boundary caused by the bolt. The effect of the weighted matrix and the proportion of on the convergence results are discussed.
References
-
Ritto T. G., Sampaio R., Aguiar R. R. Uncertain boundary condition Bayesian identification from experimental data: A case study on a cantilever beam. Mechanical Systems and Signal Processing, Vol. 68, Issue 69, 2016, p. 176-188.
-
Friswell M. I., Wang D. The minimum support stiffness required to raise the fundamental natural frequency of plate structures. Journal of Sound and Vibration, Vol. 301, Issues 3-5, 2007, p. 665-677.
-
Goedecke A., Jackson R. L., Mock R. A fractal expansion of a three dimensional elastic-plastic multi-scale rough surface contact model. Tribology International, Vol. 59, 2013, p. 230-239.
-
Belghith S., Mezlini S., Belhadj Salah H., et al. Modeling of contact between rough surfaces using homogenisation technique. Comptes Rendus Mecanique, Vol. 338, Issue 1, 2010, p. 48-61.
-
Cao Z. F., Fei Q. G., Jiang D., et al. Nonlinear normal modal analysis of flexible structures with nonlinear hinge. Journal of Vibration Engineering, Vol. 31, Issue 4, 2018, p. 573-581.
-
Pabst U., Hagedorn P. Identification of boundary conditions as a part of model correction. Journal of Sound and Vibration, Vol. 182, Issue 4, 1995, p. 565-575.
-
Yang H. T., Yang B., Li H. T. Numerical solution of multi-variables inverse problem for a beam with elastic boundary supports. Journal of Dalian University of Technology, Vol. 51, Issue 4, 2011, p. 469-472, (in Chinese).
-
Wang S. Model updating and parameters estimation incorporating flexible joints and boundary conditions. Inverse Problems in Science and Engineering, Vol. 22, Issue 5, 2013, p. 727-745.
-
Yang T. C., Fan S. H., Lin C. S. Joint stiffness identification using FRF measurements. Computers and Structures, Vol. 81, Issues 28-29, 2003, p. 2549-2556.
-
Baruh H., Boka J. B. Modeling and identification of boundary conditions in flexible structures. International Journal of Analytical and Experimental Modal Analysis, Vol. 8, 1993, p. 107-117.
-
Jiang D., Zhang D. H., Fei Q. G., et al. An approach on identification of equivalent properties of honeycomb core using experimental modal data. Finite Elements in Analysis and Design, Vol. 90, 2014, p. 84-92.
-
Jiang D., Li Y. B., Fei Q. G., et al. Prediction of uncertain elastic parameters of a braided composite. Composite Structures, Vol. 126, 2015, p. 123-131.
-
Mottershead J. E., Friswell M. I., Ng G. H. T., et al. geometric parameters for finite element model updating of joints and constraints. Mechanical Systems and Signal Processing, Vol. 10, Issue 2, 1996, p. 171-182.
-
Schmidt A., Bograd S., Gaul L. Measurement of join patch properties and their integration into finite-element calculations of assembled structures. Shock and Vibration, Vol. 19, Issue 5, 2012, p. 1125-1133.
-
Jiang D., Wu S. Q., Shi Q. F., et al. Parameter identification of bolted-joint based on the model with thin-layer elements with isotropic constitutive relationship. Journal of Vibration and Shock, Vol. 33, Issue 22, 2014, p. 35-40.
-
Jiang D., Shi Q. F., Fei Q. G., et al. Stiffness identification of fixed bolted-joint interface. Journal of Solid Rocket Technology, Vol. 37, Issue 5, 2014, p. 688-693.
-
Desai C. S., Zaman M. M., Lightner J. G., et al. Thin-layer element for interfaces and joints. International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 8, Issue 1, 1984, p. 19-43.
-
Jiang D., Wu S. Q., Shi Q. F., et al. Contact interface parameter identification of bolted joint structure with uncertainty using thin layer element method. Engineering Mechanics, Vol. 32, Issue 4, 2015, p. 220-227.
About this article
The work described in this paper was supported by the National Natural Science Foundation of China (No. 11602112).
