Abstract
The paper deals with the mathematical modeling of the controlled motion of an automatic underwater vehicle under conditions of inaccuracy and uncertainty of information support. Methodological and theoretical approaches based on the application of the principle of complexity and fuzzy logic are proposed.
1. Introduction
One of the most effective and frequently used technical means for the development and study of the oceans are automatic underwater vehicles (AUV) [1]. Their main advantages are: the ability of independent spatial maneuvering, the ability to simultaneously perform a wide range of underwater work, a high level of automation of standard work operations, mobility and autonomy. The solution of the tasks is ensured by AUV with the help of various subsystems combined into a single control system. Within the framework of this system, the dynamic modes of AUV operation is supported by the information control complex and a high-performance computing environment.
The motion control system is an important element of the information and control complex of the underwater vehicle. This system implements one purposeful spatial maneuvering, and also provides a given mode of movement. During designing a motion control system, the accepted mathematical model of the AUV as an object of dynamics and control has the main influence on the achievement of control objectives. Accounting for the properties of all elements of the information and control system allows us to conclude that the underwater vehicle is a “complex” control object [2]. Modeling of complex objects is a time consuming and expensive process. In practice, simplified models are used. In the process of models simplifying, the inaccuracies and uncertainties of the information used to create the information and control complex increase. As a result, the software for the underwater vehicle based on which control signals are generated contains incorrect information. Practical implementation of the methods of accounting for “complexity” in the mathematical description of the underwater vehicle as a control object in the design of a control system will improve the quality and accuracy of achieving of the control goal – implementing the required maneuvering and ensuring of its predetermined movement. To do this, it is rational to apply new approaches, formalisms and methods of modern control theory, focused on the application of the complexity principle [3] and the concept of soft computing [4], including the theory of fuzzy sets, artificial neural networks and genetic algorithms.
2. The principle of complexity in mathematical modeling of the motion of an automatic underwater vehicle
A variety of options for the practical use of various types of underwater vehicles is based on existing technical support for the process of achieving of the required system-wide operating goals. Managed spatial movement of the AUV is implemented in accordance with the desired motion mode, during which the specified types of trajectories are realized.
The consequence of this is the presence of elements of information support of such non-factors as inaccuracy and uncertainty. The practical implementation of this approach to modeling the AUV shows that the incompleteness of the mathematical description of the control object and supporting the controlled dynamic information support process affects the characteristics of the motion control system.
The elements of information support, formalized by using fuzzy sets include AUV parameters, its equations of motion, a quantitative description of the inaccuracy and uncertainty of information elements, and other information depending on the specific type of AUV and features of its operation. The object parameter values and the laws of their changes are considered unknown, but there is some information about the preference of certain values of their elements, which allows us to determine some convex set . Then the mathematical description of the AUV has the form of differential inclusion:
where is the state vector of the AUV; – control vector; – AUV parameter vector; – vector function; – time; , , – known compact convex sub-sets of the corresponding spaces; – the time interval at which the controlled process of the movement of the AUV is simulated.
The output of the AUV model based on Eq. (1) is characterized by the observation vector , , which belongs to the set , , called the observation space.
The observation model is a functional interrelation of elements with and vector in the form , where is a known vector function.
When constructing a mathematical description of the AUV, a certain initial set of models is formed, from which the preferred option is selected. When forming of model set, it includes only those models that meet the stated goal of modeling.
The selected models are combined into the initial set , on which the possibility of element comparing among themselves for the analysis of preference can also be determined. Each is assigned to the purpose of modeling . The relation denoting the purpose of the simulation is a binary equivalence relation, . For some elements , , a partial order ratio can also be specified. The set of all model s that have a common goal of modeling with the equivalence relations defined on this set is called the target model space (TMS) of the controlled AUV. Then the TMS has a tuple , provided that , and set is closed.
In addition, with the TMS a variety of attributes of models (VAM), included in this space is used. All elements of VAM are reduced to the terms of the abstract finite alphabet . From the symbols of this alphabet, words and word combinations are composed using a stitching operation. Then, the description of VAM corresponds to a universal set of words expressing all the properties of the model .
Part of the properties , called non-specific, is established by analyzing the model itself without involving other elements. The set of non-singular words along with the operation of stitching is called the model appearance space (MAS). Special call properties, the presence of which can be established only by comparing of the model with the elements of a certain subset . The set of such words and the operation of stitching is called the criterial space of models (CSM).
The MAS and CSM spaces for a specific TMS are formed on the basis of the display of the entire input information set of information elements available at the modeling stage of the AUV controlled information set to characterize the set of information intended for the formation of the TMS and model selection .
In modeling, an equivalence is introduced. characterizes the complexity of models which correspond to specified conditions and requirements. This allows you to create a family that is a cover of the TMS and represents a decomposition in complexity. The complexity functional is a mapping where a subset characterizes a quantitative estimate of proximity to . The model has minimal complexity. For functional complexity is indicated . In mathematical modeling, taking into account the complexity principle, the problem of multicriteriality can arise. This necessitates the use of equivalence on lexicographic complexity.
The principle of complexity is formulated as follows: in a given main ideal of the element of the decomposition of the TMS taking into account complexity of it is necessary to find an element with the required property defined in the CSM. With the help of the complexity functional, the complexity principle is written as , , where is the principal ideal of the decomposition of the space generated by the level sets of the functional ; – specified level of complexity.
The set of representatives of the level sets of the complexity functional is taken as the scale of complexity , .
Taking into account inaccuracy and uncertainty , it is proposed to determine the elements of the TMS on its basis in the class of fuzzy models, in which the input words correspond to the desired control, and the output – to the states of the dynamic system whose behavior is described by the model. In this case, a generalized description of a fuzzy model can be represented as a sequence of fuzzy operators that correspond to fuzzy production rules based on a fuzzy implication operation. Such model representation can be written as:
where – fuzzy sets belonging , with given membership functions , ; – a fuzzy state vector defined by the production rule with a number ; – fuzzy display of the consequent part of the product, which characterizes the local dynamics of the AUV; – number of rules. A clear output Eq. (2) is calculated in accordance with the selected defuzzification method.
Thus, the mathematical description of the AUV requires a theoretical solution of the complex of problems, the structure of the relationship between them is illustrated in Fig.1.
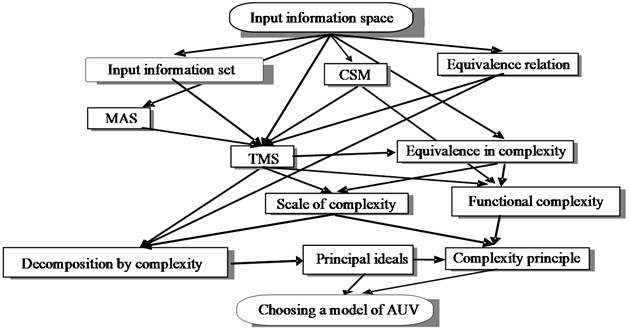
Fig. 1. The structure of the mathematical description of the AUV on the basis of the complexity principle
The elements of the structure reveal the following sequence for solving of the research problem:
• formation of the input information space based on the AUV modeling;
• design of an input information set;
• description of fuzzy information elements that form the project information space, combining VAM and CSM;
• selection of the purpose of modeling and equivalence relations;
• construction of a mathematical description of the TMS;
• determination of the equivalence relation by complexity, partitioning of the TMS into related classes and factor sets by complexity, choice of scale and complexity functional;
• decomposition of the TMS, VAM and CSM with respect to equivalence in complexity, the definition of the main ideals for the elements of the decomposition of the TMS;
• formalization of the complexity principle;
• model selection from the corresponding decompositions of the TMS;
On the basis of the chosen model, the tasks of analyzing of the AUV dynamics are solved.
The approach requires the specification of the complexity principle and its practical application using the basic elements of “soft” calculations for mathematical modeling of the controlled motion of the AUV.
3. Mathematical description of the input information space
To construct a TMS, VAM, CSM and substantiate the choice of the complexity principle, the input information space should combine, along with the stitching operation , elements of information support, with the help of which the controlled motion of a dynamic object is described.
Traditional dynamic models of the AUV should be focused on the formation of a TMS, the elements of which model the behavior of the control object solving a set of management tasks. For this, a mathematical description based on the theory of the dynamics of a rigid body moving in a viscous fluid is usually used.
The spatial orientation of the object is described by Euler angles: yaw , pitch and roll . To describe the kinematic parameters, linear and angular velocity vectors are introduced. The position vector is defined as , where is the vector of the coordinates of the AUV pole; – vector of Euler angles. The velocity vector can be written as .
The controlled motion of the AUV is described by a system of differential equations, which in the vector-matrix form is:
where is the inertia matrix of AUV as a solid; – matrix of Coriolis and centrifugal forces of a solid; – matrix of added masses; – hydrodynamic matrix, similar to the matrix of Coriolis and centrifugal forces; – matrix of forces and moments of viscous friction; – the vector of forces and moments caused by gravity and buoyancy; and – kinematic matrices describing the relative rotations of the corresponding coordinate systems; – the vector of forces and moments created by the controls of the AUV.
For a quantitative assessment of inaccurate and uncertain parameters it is proposed to use triangular numbers.
In this regard, the vector of parameters is represented by a tuple , where is a vector of nominal values of parameters, a is an interval vector, or , , where is a fuzzy number; , – respectively, the upper and lower limits of the interval ; – nominal value of the parameter.
The mathematical description of the controlled motion of the AUV in the form of taking into account the intervaliness allows us to form the inclusion and the equation.
The method of forming of the set of possible phase trajectories in the state space based on a series of computational experiments on model Eq. (1).
Each interval is approximated by a finite set of points that are elements of a set . The number of elements is equal to . The series of computational experiments consisting in solving the Cauchy problem for forms set of phase trajectories The values in moments determine the information sets . The input information set is proposed to be formed by approximating with ellipsoids, which have the form:
where is a positive-definite symmetric matrix with size ; – vector of coordinates of the center of the ellipsoid of dimension.
The definition of the matrix and the vector is made from the condition of minimizing the volume of the ellipsoid . For this, the optimization problem is solved using nonlinear programming methods:
where denotes the scalar product of vectors.
The study of the time variation of the characteristic dimensions of the approximating ellipsoids Eq. (6) is performed using the criterion:
where are the diagonal elements ; – the normalizing vector of dimension .
The obtained results demonstrate the possibility of forming an input information space sufficient for fuzzy model constructing. Mapping of the input space to fuzzy VAM and CSM to design the TMS, select the initial model from it and analyze the stability of the AUV motion on its basis.
A level set is introduced, which includes vectors , – sets of matrix elements , an ellipsoid , characterizing the “tube” in space with the central axis in the form .
The set of admissible domains in the set is partially ordered by nesting. The unit is the whole set . Chains of nested sets form the main ideals in the set . Full ordering of set and set can be implemented lexicographically for the alphabet .
The quality functional is reduced to satisfying the constraints on the model output, i.e. for all , , the following condition is implemented:
To solve the problem, the principle of complexity is applied in the form , .
The set of representatives of the level sets of the complexity functional is taken as the scale of complexity.
The result of the mapping is determined by the TMS, which combines the algorithmic description of the fuzzy model Eq. (2). Output variables , , are treated as linguistic variables.
To estimate the measure of proximity of fuzzy models, it is proposed to use a fuzzy relationship, reflecting the degree of confidence that the models under consideration have adequate properties. For this, the concept of fuzzy measure of proximity of models is introduced. Adequacy assessment is performed by the value of the index of the function of belonging . The function based on the well-known information sets and is formed.
A measure of the proximity of the outputs of the differential inclusion and fuzzy models and at the time is .
According to the principle of generalization [5], L. A. Zadeh the membership function of a fuzzy proximity measure is calculated by the formula:
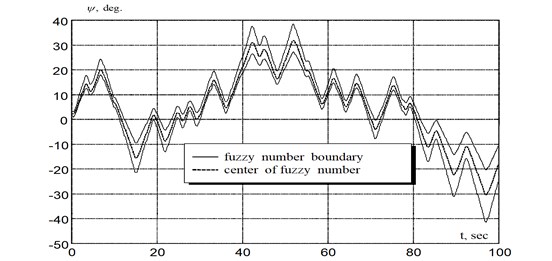
On the basis of the differential inclusion Eq. (2), a computational experiment is organized to simulate the dynamics of the AUV with fuzzy elements of the parameter vector . The simulation result for the underwater vehicle “AFALINA” [1] is shown in Fig. 2.
Thus, the theoretical and methodological issues of the synthesis of the algorithmic description of mathematical models of the controlled motion of the AUV based on the complexity principle are considered. The mapping of the input information space to the spaces of the TMS, VAM and CSM, sufficient to select a model that meets the requirements for complexity, is given.
Fig. 2Results of modeling fuzzy dynamics of underwater vehicle “AFALINA”
4. Conclusions
A feature of the practical application of modern complex AUV is the increasing requirements for the quality of their purposeful functioning under conditions of objectively increasing the level of uncertainty, like a priori information about the system and its operating conditions used in the design, and information collected by the system about its current state and environment direct performance of underwater work. The recognized direction of solving the problem of compensating the influence of inaccuracies and uncertainties of the information used on the dynamic capabilities of the AUV is to improve the methods of its mathematical modeling as a control object. This assumes the use of effective information technologies developed in the theory of artificial intelligence, and intended for use in inaccurate and uncertain information support. Therefore, the actual scientific and technical problem is the development of mathematical modeling methods that take into account the modern principles of describing the properties of information used in modeling and the implementation-oriented results of its practical application in the next-generation computing systems.
References
-
Siek Yu L., Smolnikov A. V., Yakovleva M. V. Controlling an Underwater Robot Based on Fuzzy Logic: a Monograph. SPbGMTU, St. Petersburg, 2008, p. 185.
-
Siek Yu L., Soe Min Lwin Simulation of the controlled movement of a marine dynamic object based on the complexity principle. Proceedings of the XVI All-Russian Scientific Conference “Telematics-2009”, 2009.
-
Solodovnikov V. V., Tumarkin V. I. The Theory of Complexity and Design of Control Systems. Science, Moscow, 1990, p. 68.
-
Nechaev Yu I. Fuzzy knowledge system for estimation of ship seaworthiness in onboard real time intelligence systems. Proceedings of 16th International Conference on Hydrodynamics in Ship Design, Poland, 2005.
-
Zadeh L. A. A Theory of Approximate Reasoning. Machine Intelligence, Vol. 9, Elsevier, New York, 1979, p. 149-194.
-
Sokolov S., Zhilenkov A., Chernyi S., Nyrkov A., Mamunts D. Dynamics models of synchronized piecewise linear discrete chaotic systems of high order. Symmetry, Vol. 11, Issue 2, 2019, p. 236.
