Abstract
The process of motion transmission in mechanisms consisting of two links connected by straight stems is considered. The Zener phenomelogic model was used, where the phenomena of relaxation and retardation are taken into account. It is shown that the elastic properties of a substance should be considered as a complex function. A new system of differential equations is presented, which explicitly describes the oscillations of the speeds of movement and stresses in the body. It is shown that the new method allows to take into account the degree of distribution of the parameters of force lines, and for short lines it makes it possible to describe the dynamics with simple expressions.
1. Introduction
Any simplest mechanisms for transferring motion (translational or rotational) can generally be represented as input and output links interconnected by a force line. Such connecting lines can be of various lengths and are made of different materials. For example, in a mechanical drive, metal shafts are used as a force line, and in a hydraulic drive - hydraulic lines. When motion is transmitted from the input link (engine) to the output link (executive body), longitudinal or torsional oscillations occur in the mechanism, which lead to a deviation from the specified law of motion.
A lot of work is devoted to the study of oscillations of a mechanical system. Among the many works one should single out the manuscript [1], which summarizes the methods for studying the motion of a rigid body and gives solutions of differential equations for finding free and forced vibrations. In addition, in many cases the problem of longitudinal vibrations of rods formally reduces to solving a differential equation in the problem of longitudinal vibrations of a string [2].
To study the dynamic characteristics in the mechanisms of transfer of translational and rotational motion, as models we take a rod, at the end of which a disk or mass is attached (Fig. 1).
Fig. 1Models of a rod with a mass at the driven end: a) with longitudinal vibrations, b) with torsional vibrations; F2, Mr is respectively, force and moment of resistance. Here: 1 is input link; 2 is output link; 3 is force line
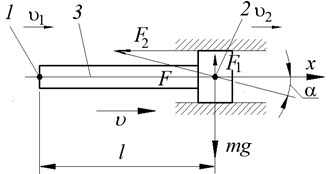
a)
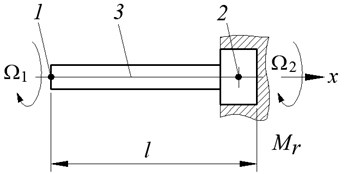
b)
2. Analysis of the movement of particles of an elementary volume of a cylindrical stem
On the issue of motion transmission in mechanical systems, there are a number of Maxwell, Voigt, Zener phenomelogical models. We consider the more general Zener model [3, 4], Fig. 2.
Fig. 2Zener rheological model: θ – deformation; η – viscosity; σ – normal tension; t – time; E1, E2 – isothermal and adiabatic modulus of elasticity, respectively
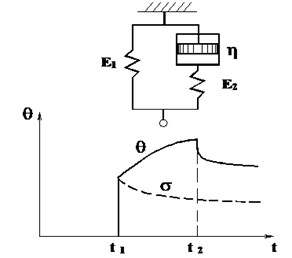
Here it is assumed that there is a body that, under the action of tension, is elastically deformed and at the same time can flow. When stress is applied, when , the springs are instantly deformed by magnitudes / and /, and the piston starts to move evenly with speed (/)/. The differential equation is written in the form:
After some transformations and transition under zero initial conditions to the Laplace transformations, it is possible to obtain a function that, in a generalized form, characterizes the elastic properties of the substance [3]:
here is relaxation time under the condition of constant deformation; is s-complex variable; is circular frequency. After substituting in Eq. (2) we get:
From the above expressions it follows that in the general case the modulus of elasticity should be considered as a complex function. Using the well-known wave equations [5], derived from the Lamé equations [6] and the equations of momentum and angular momentum [5], equations were derived that in explicitly form describe the vibrations of motion speeds and stresses in the elementary volumes of rods:
here we introduce the notation. For torsional vibrations: is angular velocity, is maximum tangential stress, is radius of the rod section; .
For longitudinal oscillations: is displacement velocity, is normal stress, .
In Eqs. (6) , is static elastic moduli and shear; is density of the material. Real lines of force made of solids are more accurately characterized as a viscoelastic material. The process of deformation of its unit cell is described by Eq. (1) [7].
2.1. Method of research. Theoretical aspect
With longitudinal harmonic oscillations in an isotropic body, a flat longitudinal sinusoidal wave propagates in the positive direction from the source of oscillations, the equation of which has the form [8]:
where is potential of the velocity of the disturbed motion of the medium; is cyclic frequency of oscillations; is wave number, /; is wave amplitude; is initial phase of oscillations points of medium.
If a wave propagating in a certain medium reaches the interface of this medium with another medium, then reflection, refraction or absorption of this wave may occur. Features of the interaction the wave with the interface of the media is largely determined by the wave resistance. For solids in the physical encyclopedia [9], such resistance is defined as the ratio of the voltage with the opposite sign to the velocity of the medium in a wave of oscillations:
here is the speed of sound in the line. From the manuscripts [8, 9] it follows that , , where is Poisson’s ratio.
If we consider the harmonic oscillations propagating along the force line, then mechanical impedance in the operator form is into consideration, taking into account Eq. (7), can be represented as [7]:
We note that the ratio / is characterizes the magnitude of internal friction, and determines the phase by which the change in strain is ahead of the change in stress.
When , 1, this expression will have the form:
here:
Dynamic features of lines with parameters distributed along the length are characterized by the operator coefficient of wave propagation, which in Laplace images can be written in the form [7]:
Usually, internal friction is neglected, i.e. 0.
Since the relaxation time constant is small ( 10-8 – 10-9 sec), it can be seen from Eq. (4) that for a sufficiently wide frequency band, one can take 0.
Then when , , the wave impedance will be:
Conducting under zero initial conditions, one-dimensional Laplace transform [10] Eqs. (5) for longitudinal oscillations and taking into account that with the accepted assumptions:
The solution of the system of Eqs. (13) allows to find for the selected section instantaneous deviations from the steady-state values of stresses and speed of movement of the sections of the rod, depending on the physical and geometrical properties of the line [7].
We present the final solution of the system of Eqs. (13) for the mechanism transmitting translational motion, under the corresponding boundary conditions [7], Fig. 1(a):
here:
Eqs. (14), (15) allow determine various frequency characteristics. Below is one of such characteristics (), illustrating the effect of a change in the longitudinal velocity of the input link on the change in normal voltages in the power line near the output link in the absence of a resistance force ( 0) [7]:
here is the sectional area of the trunk at the executive body of mass ; , , is coefficients of friction loss and resistance force acting on the executive body; is the length of the line.
In view of (16) we have //, where , then then functions not complex functions [7]. From the analysis of the function Zn () follows: with 0, 1; for /2 + > > + , < 0. Here 0, 1, 2, ...., .
This means that at 0 ≤ ≤ 1, the wave processes in the lines can be neglected.
This conclusion was first published in [7]. The papers [11-13] give solutions using Eqs. (17) for the mechanisms of rotational motion transmission, Fig. 1(b).
Using Eqs. (14)-(27), neglecting for simplify of the line parameters distribution and applying the well-known methods of the theory of functions of a complex variable, one can obtain simple expressions describing motion.
So, for example, in the case of an abrupt change in the force and at 0 as a result of the solution using the theorem of residues, the speed of movement of the executive body is described by the expression:
here is inertial constant is damping coefficient, [7].
If it is impossible to neglect the distributed parameters, then it is advisable to apply the method of numerical solution to determine the quantitative characteristics [14].
For example, to study the dynamics of the mechanism, where instead of the rod (Fig. 1(a)) a spring was used, a special program was developed on the basis of Eqs. (4) that made it possible to calculate the oscillations of the speed motion of the mass. The result of the calculation is shown in Fig. 3.
Fig. 3Calculated oscillogram of the transition process
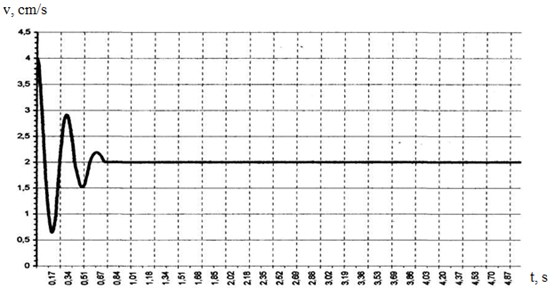
The proposed method was applied to the study of dynamic processes for two-link and three-link mechanisms in relation to the technology of manufacturing deep holes. The zones of stable and unstable operation of the mechanism were identified and the cutting conditions were optimized [15].
3. Conclusions
The proposed method for studying dynamic processes in mechanical systems shows ways to study the oscillations of speeds and stresses in fairly complex systems that have both distributed parameters and nonlinearities. In linear systems, where the distribution of parameters can be neglected, this method allows one to obtain fairly simple solutions, where for answering specific questions one can make engineering calculations using calculators.
References
-
Routh E. J. The Advanced Part of a Treatise on the Dynamics of a System of Rigid Bodies. Macmillan and Co, London, 1884.
-
Lur’e A. I. Operational Calculus and Its Applications to Problems of Mechanics. GITTL, Moscow, 1950.
-
Reiner M. R. Rheology. Encyclopedia of Physics. Springer, Berlin, Germany, 1958.
-
Postnikov V. S. Internal Friction in Metals. Metallurgiya, Moscow, 1974.
-
Sedov L. I. Continuum Mechanics. Vols. 1, 2, Nedra, Moscow, 1970.
-
Bateman H. Higher Transcendental Functions. Vols. 1-3, McGraw-Hill Book Company, 1953.
-
Kondratenko L. A. Vibrations and Speed Regulation Methods of Movement of Technological Objects. MRSU, Moscow, 2005.
-
Yavorskij B. M., Detlaf A. A. Handbook of Physics, Nauka, Moscow, 1965.
-
Prohorov A. M. Physical Encyclopedia. Vol. 4, Moscow, 1994.
-
Ivanov V. A., Chemodanov B. K., Medvedev V. S. Mathematical Foundations of the Theory of Automatic Control. Vysshaya Shkola, Moscow, 1971.
-
Kondratenko L., Mironova L., Terekhov V. Investigation of vibrations during deepholes machining. Journal of Vibroengineering Procedia, Vol. 11, 2017, p. 7-11.
-
Kondratenko L. A., Mironova L. I. Features of the transfer of motion in the expansion of heat-exchanging tubes in nuclear power plants with the help of rollers. Engineering and Automation Problems, Vol. 2, 2017, p. 135-142.
-
Kondratenko L., Mironova L. Features of loss of stability of the work of two-link mechanisms that have an infinite number of degrees of freedom. International Journal of Mathematical, Engineering and Management Sciences, Vol. 3, Issue 4, 2018, p. 315-334.
-
Kondratenko L., Mirinova L., Dmitiev V., Kuznezova E. Mathematical modeling of dynamic processes in essentially nonlinear mechanical systems with lumped parameters. Journal of Periódico Tchê Química, Vol. 15, 2018, p. 126-137.
-
Kondratenko L., Mirinova L. Mathematical model of the process of processing a considerable quantity of apertures on CNC machines. Engineering and Automation Problems, Vol. 4, 2018, p. 80-87.
