The dynamic-selfsimilar lattice as the vibroisolation systems

1. Introduction

The lattice structures are often used as vibroisolation systems. Their main advantage is the possibility of vibration damping and the ability to withstand the significant static loads [1, 2]. On Fig.1a a planar lattice structure with a periodic structure is presented. It can also be considered as a lattice filter element. Due to the periodicity of the lattice structure is characterized by the alternating of the passband and non- passband. In the non-passband, the harmonic signal propagates with the great attenuation. Therefore, these lattices are called as the mechanical band-pass filter. Lattice structures, both beam and plate, were theoretically and experimentally investigated in [1, 3]. They have been studied the lattices wave properties, the passbands depending on the angle of wave propagation, and the estimates of their effectiveness are received.

However, as studies [4, 5] have shown the stronger vibro-isolation properties have the systems with dynamic self-similarity structures. In this paper the wave properties of such systems are investigated, the non-passbands and the attenuation intensity for the harmonic signal are determined.

First, we define the concept of the dynamic self-similarity (dynamic fractal) and introduce the corresponding analytical criteria.

2. Dynamic-selfsimilar structures (dynamic fractals). Definition

Currently, the geometric fractals of Mandelbrot are well known [6, 7].

“Selfsimilarity, invariance with respect to scaling (or scaling)” invariance with multiplicative scale changes. In short, a self-similar object looks unchanged after increasing and decreasing its size (Mandelbrot P. [6])”.

“Fractal – a term meaning a geometric figure that has the property of selfsimilarity, which is composed of several parts, each of which is similar to the whole figure as a whole”.

As follows from these definitions, the Mandelbrot’s fractals describe the structures which similar in geometric parameters (scaling), that is, they are geometric fractals. The study of such systems is devoted to a large number of works, including computer studies relating to the formation [8]. The study of the wave and acoustic properties of fractal structures dedicate the works of L. M. Lyamshev, V. V. Zosimov, I. A. Urusovskii [9-12]. In these works, the elastic vibrations and waves in materials with geometric-fractal structure are investigated, their dispersion equations are found. The oscillations of fractal clusters characterized by the dependence of their elastic properties on the scale are also studied.

Fig. 1a) A lattice with the periodic structure, b) the dynamic-selfsimilar lattice (dynamic fractal)

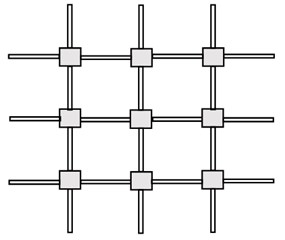
a)

b)

However, the dynamic properties of the system determine its elastic-inertial parameters. Therefore, it is interesting to study the dynamic properties of structures consisting of cells which similar not in geometric but in dynamic parameters. For this purpose, it is necessary to introduce the concept of dynamic fractal. To this end, it is logical to require the parameters scaling determining the dynamic properties of the system, i.e. its elastic and inertial parameters [4, 5]. It’s a completely different kind of structures that are different from the Mandelbrot’s fractals. Dynamic fractals reflect the dynamic (not geometric) properties of the system and therefore they describe well the dynamic and wave properties.

Definition. We call the dynamic-selfsimilar structures in which their elastic and inertial parameters change with the same scale $\gamma$ for each $s$th cell of the structure (or subsystem):

where $K_s$ – is stiffness, $J_s$ – is the inertia parameter of the $s$th cell.

A necessary consequence of the conditions Eq. (1) is equality of the partial frequencies for all forming cells:

The condition of the equality for partial frequencies Eq. (2) is a condition for the dynamic selfsimilarity. Such structures can be called as the dynamic fractals.

The above definition of a dynamic fractal can be easily generalized to the structures in which the number of DOF for the forming cells is greater than one. In this case, each coordinate can have its own similarity factor.

Comment. Note that the conditions Eq. (2) for a dynamic fractal do not coincide with the conditions for the geometric similarity (scaling) used in geometric Mandelbrot fractals. Indeed, suppose that the elastic elements of the $s$th cell is the rod, its stiffness is equal to $\left(E{F}_s\right)/l_s$, and the inertial element is a rigid ball of radius $R$, i.e., $m_s=\left(4\rho \pi R_s^3\right)/3$ (here: $F_s$ is the cross-sectional area for the $s$th cell, $l_s$ is its length). Geometric scaling conditions have the form: $F_{s+1}={\gamma }^2{F}_s$, $l_s=\gamma l_s$, $R_s=\gamma R_s$. It is obvious that the conditions Eq. (2) for the dynamic fractal in this case are not met:

Thus, the fulfillment of the conditions Eqs. (1), (2) for a dynamic fractal requires different scaling of geometric parameters, which is a certain generalization of the geometric fractal.

On Fig. 1(a) the dynamic-selfsimilar lattice is represented.

3. The wave properties and non-pass bands for the dynamic-selfsimilar structures

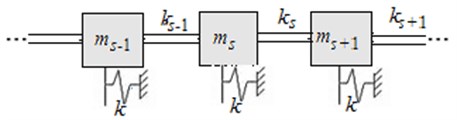
First, we study the wave properties for the dynamically-selfsimilar structures on the example of the simplest structure in Fig. 2(a), here $\gamma$ > 1. It is an unbranched chain structure in which the each $s$th cell consists from a concentrated mass $m_s$ and a spring with stiffness $k_s$.

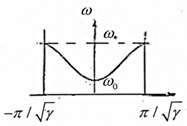
Fig. 2a) The dynamic-selfsimilar chain structure with increasing parameters (γ > 1); b) the periodic structure, equivalent in frequency to selfsimilar one, c) the dispersion curve for the chain system of Fig. 2(b), d) the partial subsystem, which determines the lowest frequency of the non-pass band, e) the partial subsystem, which determines the highest frequency of the non-pass band

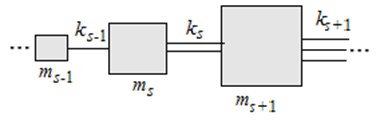
a)

b)

c)

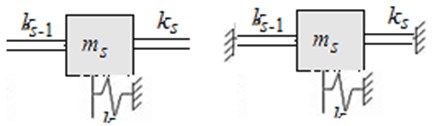
d)

Let the elastic and inertial parameters change with the same scale $\gamma$ from cell to cell (Fig. 2(a)). Then the stiffness and mass for the element $s+1$ is:

Equation for $s$th cell is the finite difference equations [13, 14]:

where ${\mathbf{X}}^T=\left[x_1,x_2,x_3,...,x_n\right]$, $x_s$ – displacement of the $s$th mass, $\omega$ is natural frequency. With $\gamma$ < 1 we obtain a structure with length-decreasing parameters, and for $\gamma$ > 1 with increasing parameters. Make the change of variables:

As a result, we find the equation for the $s$th cell in the new variables:

Eq. (6) is the same for any number s and therefore describes the periodic structure of Fig. 2(b). Indeed, the partial frequencies of each mass ${\stackrel{-}{\nu }}_s^2=\left(k_{s-1}+k_s\right)/m_s=\left(\frac{1}{\gamma }+1\right){\nu }_s^2$ are the same due to the condition Eq. (3), the stiffness between the masses is equal $1/\sqrt{\gamma }$, and there is an additional fixation of mass:

The partial solution of Eq. (6) is [15]:

$\omega$ is the natural frequency, $\mu$ is a wave parameter characterizing the phase change between the elements s and $s+1$.

From Eqs. (7), (6), we find the dispersion equation for the periodic structure Fig. 2(b). For real $\mu$:

and for purely imaginary $\mu =i\mu \text{'}$.

The linear transformation of the coordinates Eq. (5) does not change the frequency properties, so the dynamic fractal Fig. 2(a) and the periodic structure of Fig. 2(b) have the same frequency. The periodic structure is a mechanical bandpass filter with harmonic signal bandwidth equal to: ${\omega }_0$ < $\omega$ < ${\omega }^{\mathrm{*}}$ (Fig. 2(e)):

The band pass from Eq. (9) is:

It is easy to see that the lower and upper limits of the bandwidth are defined as the partial frequencies of the forming subsystems with free and fixed ends, respectively: so ${\omega }_0^2$ corresponds to Fig. 2(c) and ${\omega }^{*2}$ corresponds to Fig. 2(d).

Thus, the bandwidth is inversely proportional to the similarity parameter $\gamma$. When $\gamma$ > 1 increases, the lower limit of the bandwidth increases.

It is seen from Eq. (5) the distinctive feature of the dynamic self-similar structures with increasing parameters: in the non-pass band, the decrease in the oscillations level is significantly higher than in the periodic one. It allows increase the effectiveness of vibroisolation and reduce the lattice size.

4. The branched structures (two-dimensional lattice) and its wave features

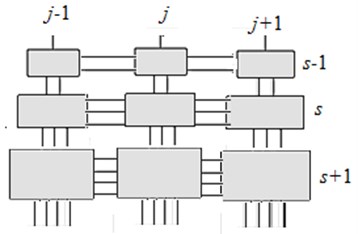
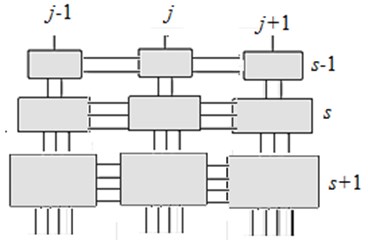
Consider now a two-dimensional dynamic-selfsimilar lattice shown in Fig. 3. Each lattice element has presently a double index $sj$, wherein s is row number (axis $x$), $j$ is column number (axis $y$).

Let’s find the conditions for lattice dynamic-selfsimilarity. For each $s$th row and for each $j$th column we assume that the elastic-inertial elements vary according to the similarity coefficient $\gamma$, i.e.:

This implies the equality of the partial frequencies:

Equation of oscillations for $sj$th lattice element has the form:

Suppose for certainty that the lattice is formed by the rod elements, that is:

By virtue of Eq. (11) the vibrations along the $x$ and $y$-axis are independent. Then from Eq. (10) the equation in finite differences for masses located in the $s$th column is:

Under this the dispersion equations coincide with the equations for the dynamic-selfsimilar structure shown in Fig. 1. Its bandwidth is defined similarly to the Eq. (9).

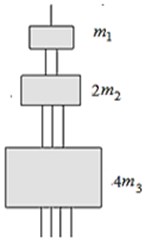
Fig. 3a) The two-dimensional dynamic fractal lattice at γ= 2, b) the dynamic fractal chain describing the oscillations in vertical plane, c) the highest natural mode in passband b)

a)

b)

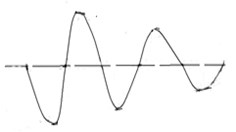
c)

5. Comparison of vibroisolation properties of periodic and dynamic- selfsimilar lattices

Despite the fact that the frequency spectrum for the periodic and dynamic fractal structure coincides, the wave propagation in them is significantly different. We study the wave behavior of a dynamic fractal inside and outside of the bandwidth. The solution for the fractal structure, given the coordinate transformation Eq. (5), is:

In the bandwidth for the periodic structure Fig. 1(b) the highest vibration mode is known as a sine wave, in which the neighboring masses are in the ant phase. The wave in the dynamic fractal structure, as seen from the coordinate transformation Eq. (5), obtained from the corresponding wave in the periodic structure of Fig. 1(b), by proportionally increase in the oscillations amplitude for each $s$th section in ${\left(\sqrt{\gamma }\right)}^s$ times. Therefore, for the dynamic fractal we receive the wave with decreasing amplitude (Fig. 4(b)). The envelope of this wave is the exponent. Thus, for a dynamic self-similar lattice in the passband is a decrease in the vibration level also in contrast to the periodic structure.

As for the non-pass band, in the periodic structure, as is known, there is an exponential attenuation of the harmonic signal along the chain at the rate of $\mathrm{e}\mathrm{x}\mathrm{p}\left(\mu \right)$ [14, 15]:

But, in a self-similar structure at $\gamma$ > 1 (Fig. 4(a)), (as follows from Eq. (12) there is an increase in the decay rate equal to $\mu +\alpha$. Thus, at $\gamma =$ 1.3, the decrease in the oscillation amplitude occurs almost 1.15 times, (15 %) faster in each row of the lattice. Therefore, it is possible to achieve the necessary level of vibration amplitude reduction using a lattice with a fewer rows.

6. Conclusions

1) The dynamic-selfsimilar lattice is frequency equivalent to the lattice with periodic structure with additional fastening.

2) The dynamic-selfsimilar lattice with -increasing parameters exhibits the vibroisolation properties in the whole range, both in the passband and outside it (in contrast to the periodic lattice).

3) In the non-pass band, the decrease of the oscillations amplitude in the dynamic-selfsimilar lattice is higher than in the periodic one, and depends on the similarity coefficient.