Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization

Jiao, Renqiang; Nguyen, Vanliem

doi:10.21595/vp.2019.20994

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2019

Check for updates

Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization

Renqiang Jiao¹

Vanliem Nguyen²

^{1, 2}School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi, 435003, China

Corresponding Author:

Vanliem Nguyen

Cite the article Download PDF

Downloads 1411

CrossRef Citations 3

Abstract

Hydraulic mounts can provide a better vibration attenuation performance than elastomeric mounts especially in the low frequency range. However, it is incapable of providing a response-dependent damper for the mount system to improve the ride comfort. In this study, a semi-active hydraulic cab mount (SHM) with control optimization was designed to improve ride comfort for the heavy vibratory roller. And a 7-DOF non-linear dynamic model of the vehicle was established for evaluation of the performance of hydraulic cab mounts based on different control optimization algorithms. To simulate roughness height the ISO level D road surface and deformed soil model were employed under the compaction work condition. The optimization study for two performance objectives as measured by responses of the vertical driver’s seat and cab pitch angle was carried out. It was shown that the SHM optimized by the fuzzy logic and proportional, integral, derivative controller methods (FLC-PID) giving best optimum values of the objective vector as compare to by multi-objective genetic algorithm (MOGA) and PID controller based on genetic algorithm (GA-PID).

1. Introduction

The cab isolation mounts performance of the vibratory roller is an important factor affecting the reliability of the roller, the comfort of operation, the noise level and the service life of the components. Therefore, improving the performance of the vibration isolation mounts system of the vibratory roller has an important role in improving the performance of the vibratory roller.

The design parameters of cab rubber mounts on the single drum vibratory roller ride comfort was analyzed by Ario Kordestani et al. [1]. Vibration analysis and improve the cab rubber mounts of vibratory roller via three cab’s isolation mounts including rubber, hydraulic, and pneumatic mounts to increase the ride comfort was studied [2]. The research results show that vibratory roller’s ride comfort is significantly increased by the hydraulic mounts (HM). Whereas, the ride comfort of the cab is still poor in condition of the vehicle moves.

In addition, the HM was also studied and applied for engine isolation system [3, 4], and semi-active hydraulic engine mounts were developed by Min Wang et al. [5]. In order to improve the harshness of construction equipment and industrial vehicles, the HM were used for cab mounts [6, 7]. The low frequency performance of vibratory roller cab with HM was studied [2]. However, this study only considers the passive cab isolation mounts. Nowadays, the control optimization methods such as multi-objective optimization [8], FLC-PID control [9], FLC-Hinf, MR Fluid damper and Skyhook-NFLC control [10, 11] are applied to adjust the damping coefficient for the semi-active suspension system or active suspension system of vehicles and seat. It was shown that mounts with control optimization can significantly enhance the ride comfort compared with the passive.

In this study, a non-linear dynamic model of the vibratory roller cab with the HM [2] is established based on Matlab/Simulink software. The control optimization methods as the multi-objective genetic algorithm, GA-PID controller, and FLC-PID controller are applied to optimize and control the cab hydraulic mounts under different operation conditions.

2. Materials and methods

2.1. Vibratory roller model

As shown in Fig. 1. The non-linear dynamic model of a single drum vibratory roller with 7-DOF is developed. $z_{s}$ , $z_{c}$ , $z_{f f}$ , $z_{f r}$ and $z_{d}$ represent the vertical displacements of the seat, the cab, the frame-front, the frame-rear and roller drum, respectively. $ϕ_{c}$ , $ϕ_{f r}$ represent the angular displacements of the cab and the frame-rear; $m_{s}$ , $m_{c}$ , $m_{f f}$ , $m_{f r}$ and $m_{d}$ are the mass of the driver’s seat, cab, frame-front, frame-rear and roller drum, respectively; $u$ represent the semi-active damping force of hydraulic mounts. $F_{s}$ , $F_{c i}$ , $F_{d}$ and $F_{t}$ represent the dynamic reaction forces in the vertical direction of seat suspension, cab mounts, roller drum mount and tire, respectively; $q_{d}$ and $q_{t}$ are the excitations of the road surface. $l_{m}$ is the distances of the vibratory roller, ( $i =$ 1, 2; $m =$ 1, 2, ..., 8). The equation of the dynamic reaction force of driver’s seat suspension is given by:

1

F_{s} = c_{s} ({\dot{z}}_{c} + l_{8} {\dot{ϕ}}_{c} - {\dot{z}}_{s}) + k_{s} (z_{c} + l_{8} ϕ_{c} - z_{s}) .

The equations of the dynamic reaction forces of cab isolation mounts in Fig. 1(b) are given by:

2

F_{c i} = k_{r i} z_{i} + c_{r i} {\dot{z}}_{i} + f_{c i},

with:

3

f_{c i} = \{\begin{array}{l} c_{h i} |{\dot{z}}_{i}| {\dot{z}}_{i}, wit h^{} hydrauli c^{} mount s^{} (HM) \\ u_{i}, wit h^{} semi-activ e^{_{}} hydrauli c^{_{}} mount s^{} (SHM), \end{array}

where $f_{c i}$ is the damping force of HM; $k_{s}$ , $k_{r i}$ represent the stiffness coefficients and $c_{s}$ , $c_{r i}$ represent damping coefficients of seat suspension and the rubber of HM, respectively.

Fig. 1Vibratory roller dynamic model

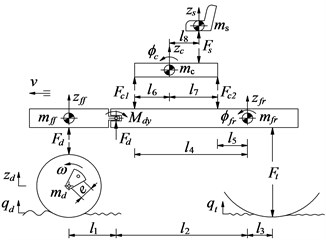
a) 7-DOF dynamic model

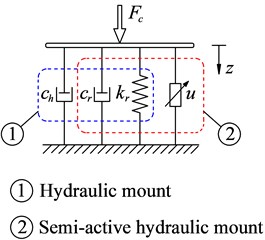
b) Model of cab mount

The relative displacements and velocities of HM are given by:

4

z_{i} = z_{b} - l_{i + 3} ϕ_{b} - z_{c} + {(- 1)}^{i + 1} l_{i + 5} ϕ_{c} .

The force equations of the roller drum ( $F_{d}$ ) and the tire ( $F_{t}$ ) are derived in Section 3. The general dynamic differential equation for the vibratory roller is given as follow:

5

\{\begin{array}{l} m_{s} {\ddot{z}}_{s} = F_{s}, \\ m_{c} {\ddot{z}}_{c} = F_{s} - F_{c 1} - F_{c 2}, \\ I_{c} ϕ_{c} = F_{s} l_{8} + F_{c 1} l_{6} - F_{c 2} l_{7}, \\ m_{f r} {\ddot{z}}_{f r} = F_{c 1} + F_{c 2} - F_{t} - F_{d}, \\ I_{f r} {\ddot{ϕ}}_{f r} = F_{d} l_{2} + M_{d} - F_{t} l_{3} - F_{c 1} l_{4} - F_{c 2} l_{5}, \\ m_{f f} z_{f f} = F_{d} . \end{array}

2.2. The vibration excitations of the vehicle dynamic model

In this study, the elastoplastic soil ground model of Adam D. and Kopf. F. [13] is chosen to establish the drum-deformed soil contact relation. In a cycle of the drum-deformed soil contact, there exist two or more often three distinct phases. The specific expression of motion can be referred to our previously published literature [2].

3. The control optimization methods

3.1. The optimal hydraulic mounts (OHM) based on the genetic algorithm

Multi-objective genetic algorithms (GA) are optimization method based on principles of natural selection. GA is defined as find a vector of decision variables satisfying constraints to give admissible to all objective functions [8], it can be written as:

Find the vector $x = {[x_{1}, x_{2}, \dots, x_{n}]}^{T}$ to optimize:

6

F (x) = {[f_{1} (x), f_{2} (x), . . ., f_{n} (x)]}^{T} .

Subject to $g_{i} (x) \leq$ 0, $i =$ 1 to $p$ ; $h_{j} (x) =$ 0, $j =$ 1 to $q$ .

$F (x)$ is objective functions, $g_{i} (x)$ is inequality constraints, $h_{i} (x)$ is equality constraints. According to the algorithm of GA [14], the structure flowchart of a genetic algorithm is shown in Fig. 2(a):

7

s . t . \{\begin{array}{l} x = {[k_{r i}, c_{r i}, c_{h i}]}^{T}, \\ 1.2 \times 1 0^{5} \leq k_{r i} \leq 9.1 \times 1 0^{5}, \\ 29 \leq c_{r i} \leq 500, \\ 4.5 \times 1 0^{3} \leq k_{r i} \leq 25 \times 1 0^{3}, \end{array}

m i n F (x) = [a_{w z s}, a_{w ϕ c}]^{T},

where $a_{w z s}$ is the weight r.m.s. acceleration responses of the driver’s seat and $a_{w ϕ c}$ is the weight r.m.s. acceleration responses of the cab pitch angle.

3.2. Design of PID controller for SHM optimized by genetic algorithm (SHM with GA-PID)

The proportional integral derivate (PID) controller is wide used in industrial process control as a result of simple structure and robust performance. The transfer function of PID can be written by:

8

u (t) = K_{p} e (t) + K_{i} \int_{0}^{t} e (t) d t + K_{d} {\dot{e}}_{d} (t),

where $K_{p}$ , $K_{i}$ and $K_{d}$ are the proportional, integral and derivative parameters, respectively.

The choose of PID parameters is significant effect the performance of PID controller [15], therefore, GA and fuzzy logic control rules are applied to calculate the optimal proportionality factors, respectively $K_{p}^{'}$ , $K_{i}^{'}$ and $K_{d}^{'}$ as follows:

9

K_{j}^{'} = \frac{K_{j} - K_{j}^{m i n}}{K_{j}^{m a x} - K_{j}^{m i n}} = \frac{K_{j} - K_{j}^{m i n}}{Δ K_{j}},

where the variable ranges of PID’s parameters are $[K_{j}^{m i n} - K_{j}^{m a x}]$ ; subscript $j$ denotes $p$ , $i$ and $d$ , respectively:

10

s . t . \{\begin{array}{l} x = {[K_{p n}^{'}, K_{i n}^{'}, K_{d n}^{'}]}^{T}, \\ 1850 \leq K_{p n}^{'} \leq 10500, \\ 100 \leq K_{i n}^{'} \leq 8500, \\ 0.1 \leq K_{d n}^{'} \leq 100, n = 1,2 . \end{array}

In order to find the optimal proportionality factors of $K_{j}^{'}$ , the variable ranges in Eq. (10) are also chosen optimally based on two objective functions in Eq. (7).

3.3. Design of PID controller for SHM based on fuzzy logic control rules (SHM with FLC-PID)

In this study, the relative displacement and relative velocity in Eq. (4), Eq. (5) of the cab isolation mount are considered as two input variables and they are denoted by E and EC, while the proportionality factors $K_{d}^{'}$ , $K_{p}^{'}$ , $K_{i}^{'}$ and are the output values, and the FLC-PID controller model shows in Fig. 2(b). The input and output linguistic variables are defined as positive big (PB), positive small (PS), zero (ZO), negative small (NS) and negative big (NB). The membership functions described by fuzzy set is the Triangular function and their values in the range of 0 and 1, both input and output values are in the [–3, 3] range.

Fig. 2The optimal control model

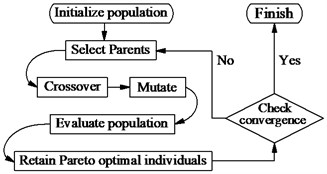
a) The flowchart of GA

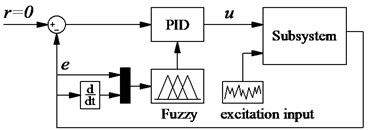
b) The FLC-PID controller

Table 1The fuzzy control rules

E

K_{p}^{'}

K_{i}^{'}

K_{d}^{'}

EC

NB

NS

ZO

PS

PB

NB

NS

ZO

PS

PB

NB

NS

ZO

PS

PB

NB

PB

PS

ZO

NB

NS

ZO

PS

ZO

PB

NS

PB

PS

ZO

NS

NB

NS

ZO

NB

NS

ZO

PS

ZO

PS

ZO

NS

ZO

PS

NB

NS

ZO

PS

ZO

NS

NB

ZO

PS

PB

NB

NS

ZO

PS

PB

ZO

NS

NB

ZO

NS

NB

PB

PS

ZO

PB

In this fuzzy controller, there are up to 25 rules, shown in Table 1, has the following expression:

1. if E = NB and EC = NB then $K_{p}^{'} =$ PB, $K_{i}^{'} =$ NB and $K_{d}^{'} =$ PS;

2. if E = NB and EC = NS then $K_{p}^{'} =$ PB, $K_{i}^{'} =$ NB and $K_{d}^{'} =$ NB;

$⋮$

25. if E = PB and EC = PB then $K_{p}^{'} =$ NB, $K_{i}^{'} =$ PB and $K_{d}^{'} =$ PB.

4. Simulation analysis

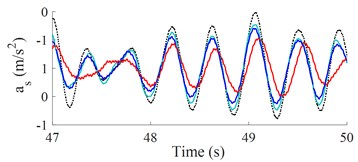
The weight r.m.s. acceleration value ( $a_{w z}$ ) and parameters of a vibratory roller in the reference [2] are used to evaluate the results. The results of the seat and cab pitch angle are shown in Fig. 3(a) and 3(b). It is shown that the $a_{s}$ and $a_{ϕ c}$ values with the control optimization methods reduced vibration and improved the cab’s ride comfort are very obvious. Besides, both $a_{s}$ and $a_{ϕ c}$ of SHM with FLC-PID also decreased compared with OHM and SHM with GA-PID.

Fig. 3The accelerations of seat and cab pitch angle

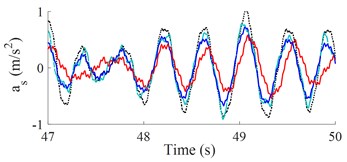
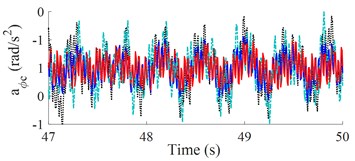
a) Low-frequency excitation of the drum ( $f =$ 28 Hz)

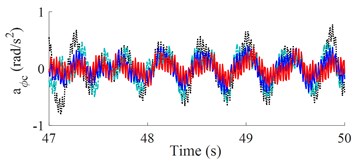
b) High-frequency excitation of the drum ( $f =$ 35 Hz)

Table 2Performance of different mounts when vehicle compacts and moves

Values		HM	OHM	GA-PID	FLC-PID	FLC-PID versus HM
$f =$ 28 Hz	$a_{w z s}$ (m/s²)	0.51	0.45	0.40	0.36	29.41 %
$f =$ 28 Hz	$a_{w ϕ c}$ (rad/s²)	0.95	0.83	0.68	0.51	46.32 %
$f =$ 35 Hz	$a_{w z s}$ (m/s²)	0.48	0.42	0.38	0.32	33.33 %
$f =$ 35 Hz	$a_{w ϕ c}$ (rad/s²)	0.88	0.72	0.63	0.43	51.14 %

Table 2 shows that the $a_{w z s}$ and $a_{w ϕ c}$ values with control optimization methods are all decreased compared with hydraulic mounts. When semi-active hydraulic cab mounts are controlled with the FLC-PID controller, the control results show that the $a_{w z s}$ and $a_{w ϕ c}$ values are greatly reduced by 29.41 % and 46.32 % when vibrating drum compacts at low-frequency excitation and reduced by 33.33 % and 51.14 % at high-frequency excitation. Moreover, the study results also show that $a_{w z s}$ and $a_{w ϕ c}$ values are significantly reduced when vibrating drum compacts at high-frequency excitation, it implies that the cab ride comfort is better when vibrating drum compacts at high-frequency excitation.

5. Conclusions

It was shown that the SHM optimized by the fuzzy logic and proportional, integral, derivative controller methods (FLC-PID) giving best optimum values of the objective vector as compare to by multi-objective genetic algorithm (MOGA) and PID controller based on genetic algorithm (GA-PID). Under the working condition of compaction, $a_{w z s}$ and $a_{w ϕ c}$ values of SHM with FLC-PID significantly decreased by 29.41 % and 46.32 % at low-frequency excitation 28 Hz and reduced by 33.33 % and 51.14 % at high-frequency excitation 35 Hz.

References

Ario Kordestani, Subhash Rakheja, et al. Analysis of ride vibration environment of soil compactors. SAE International Journal of Commercial Vehicles, Vol. 3, Issue 1, 2010, p. 259-272.

Publisher
Vanliem N., Jianrun Z., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 8527574.

Publisher
Tikani R., Vahdati et al. N. A new hydraulic engine mount design without the peak frequency. Journal of Vibration and Control, Vol. 17, Issue 11, 2010, p. 1644-1656.

Publisher
Hormoz Marzbani, Reza Jazar N., et al. Hydraulic engine mounts: a survey. Journal of Vibration and Control, Vol. 20, Issue 10, 2010, p. 1439-1463.

Publisher
Min Wang, et al. A novel design of semi-active hydraulic mount with wide-band tunable notch frequency. Journal of Vibration and Control, Vol. 333, 2014, p. 2196-2211.

Publisher
Kuzukawa M., Tanaka T. Vibration Dampening Device with an Elastic Body and Viscous Liquid. US Patent No. 5707048, 1998.

Search CrossRef
Lee P., Vogt J., Han S. Application of hydraulic body mounts to reduce the freeway hop shake of pickup truck. SAE Technical Paper Series 2009-01-2126, 2009.

Publisher
Nariman-Zadeh N., et al. Pareto optimization of a five-degree of freedom vehicle vibration model using a MUGA. Engineering Applications of Artificial Intelligence, Vol. 23, 2010, p. 543-551.

Publisher
Pekgökgöz R. K., et al. Active suspension of cars using fuzzy logic controller optimized by genetic algorithm. International Journal of Engineering and Applied Science, Vol. 2, Issue 4, 2010, p. 27-37.

Search CrossRef
Herrán Félix L.-C., Mehdi D., Ortizc Rodríguez De J.-J., et al. H_infcontrol of a suspension with a magnetorheological damper. International Journal of Control, Vol. 85, Issue 8, 2012, p. 1366-5820.

Publisher
Sy Dzung Nguyen, et al. Part 2: An application to semi-active vehicle seat-suspension system. Mechanical Systems and Signal Processing, Vol. 450, Issues 56-57, 2015, p. 288-301.

Publisher
Mechanical Vibration-Road Surface Profiles – Reporting of Measured Data. ISO 8068, 1995.

Search CrossRef
Adam D., Kopf F. Theoretical analysis of dynamically loaded soils. European Workshop Compaction of Soils and Granular Materials, 2000, p. 207-220.

Search CrossRef
Jhon Crews H., et al. Multi-objective control optimization for semi-active vehicle suspensions. Journal of Sound and Vibration, Vol. 330, 2011, p. 5502-5516.

Publisher
Zulfat H., et al. Application of self-tuning fuzzy PID controller on industrial hydraulic actuator using system identification approach. Journal on Smart Sensing and Intelligent Systems, Vol. 2, Issue 2, 2009, p. 246-261.

Publisher

Cited by

Development of cab isolation systems of off-road vibratory rollers: review research

Vanliem Nguyen | Vanquynh Le

(2020)

Study to control the cab shaking of vibratory rollers using the horizontal auxiliary damping mount

Vanliem Nguyen | Renqiang Jiao | Vanquynh Le | Peiling Wang

(2020)

Control the ride comfort of soil compactor with semi-active seat suspension and cab’s horizontal damper

Beiping Zhang | Vanliem Nguyen | Yong Wang

(2020)

About this article

Received

06 September 2019

Accepted

20 September 2019

Published

19 October 2019

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/vp.2019.20994

Keywords

vibratory roller

hydraulic mount

genetic algorithm

FLC-PID controller

Acknowledgements

This work is funded by Science and Technology Support Planning of Jiangsu Province (No. BE201433), Science and Technology Achievement Transformation Project of Nanjing (No. 201701213) and Talent Introduction Fund Project of Hubei Polytechnic University (Nos. 17xjz03R, 19xjk17R).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 03 18

Ameliorating vibratory roller quality based on two methods of cab’s horizontal damper and cab’s active suspension

Tianyuan Jiang, Vanliem Nguyen, Fan Zhang

Research article

2023 01 20

Performance of semi-active cab suspension system with different control methods

Shicheng Ni, Vanliem Nguyen

Research article

2021 02 16

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li, Vanliem Nguyen, Xiaoyan Guo, Yan Kang

Research article

2021 02 05

Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

Yan Kang, Vanliem Nguyen, Xiaoyan Guo, Yuehan Li

R. Jiao and V. Nguyen, “Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization,” Vibroengineering PROCEDIA, Vol. 28, pp. 75–80, Oct. 2019, https://doi.org/10.21595/vp.2019.20994

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.20994
UR  - https://doi.org/10.21595/vp.2019.20994
TI  - Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization
T2  - Vibroengineering PROCEDIA
AU  - Nguyen, Vanliem
AU  - Jiao, Renqiang
PY  - 2019
DA  - 2019/10/19
PB  - JVE International Ltd.
SP  - 75-80
VL  - 28
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Nguyen_2019,
	doi = {10.21595/vp.2019.20994},
	url = {https://doi.org/10.21595/vp.2019.20994},
	year = 2019,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {28},
	pages = {75--80},
	author = {Vanliem Nguyen and Renqiang Jiao},
	title = {Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]V. Nguyen and R. Jiao, “Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization,” Vibroengineering PROCEDIA, vol. 28, pp. 75–80, Oct. 2019, doi: 10.21595/vp.2019.20994.

Copy IEEE

Copied to clipboard!

Nguyen, Vanliem, and Renqiang Jiao. “Improving Ride Comfort for Vibratory Roller Utilizing Semi-Active Hydraulic Cab Mounts with Control Optimization.” Vibroengineering PROCEDIA 28 (October 19, 2019): 75–80. https://doi.org/10.21595/vp.2019.20994.

Copy Chicago

Copied to clipboard!

Improving ride comfort for vibratory roller utilizing semi-active hydraulic cab mounts with control optimization

Abstract

1. Introduction

2. Materials and methods

2.1. Vibratory roller model

2.2. The vibration excitations of the vehicle dynamic model

3. The control optimization methods

3.1. The optimal hydraulic mounts (OHM) based on the genetic algorithm

3.2. Design of PID controller for SHM optimized by genetic algorithm (SHM with GA-PID)

3.3. Design of PID controller for SHM based on fuzzy logic control rules (SHM with FLC-PID)

4. Simulation analysis

5. Conclusions

References

Cited by

About this article

Related Articles