Shadow effect compensation method for ultrasonic transducer array model

2.1. Time difference method for measuring wind speed

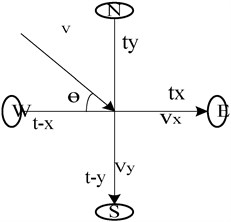
The ultrasonic wind gauge uses the classic model structure proposed by Cuerva A. and Sanz-Andres A. [4]. Four transducers are used to form two mutually perpendicular path models.

In the actual use of the ultrasonic wind meter, the time difference method is mainly used to detect the wind speed. As shown in Fig. 1, the time of ultrasonic transmission to reception in the four directions of southeast and northwest is $t_x$, $t_{-y}$, $t_{-x}$, $t_y$. By the time difference method to measure the two east-west and north-south paths wind speed ($V_x$, $V_y$):

Measuring wind speed $U$:

Assuming that the angle between the wind speed and the $x$-axis is ${\theta }_s$, the wind direction is:

The wind speed does not change during normal wind advancement. When the wind passes the sensor, the sensor blocking the shadow behind the sensor, and the other end of the sensor generates turbulence. Therefore, the wind speed $U_x$ and $U_y$ on the path must change accordingly. (The above variables represent the measured values of wind speed and angle).

Fig. 1Schematic diagram of time difference wind speed measurement

2.2. Path wind speed compensation algorithm

Data fitting is the most effective way to reduce the shadow effect by fitting a large amount of measured data to a specific ultrasonic wind meter model and fitting a curve close to the actual value [12].

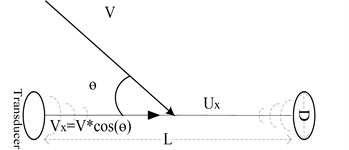
Firstly, some measuring values are defined: $V$ is the real wind speed, $U$ is the measured wind speed, $V_x$ is the projection of wind speed on the path, $U_x$ is the time difference method to measure the path wind speed, the $\theta$ is the actual Angle between the wind and the path, and the ${\theta }_s$ is the measurement Angle between the wind and the path.

Eq. (5) represents the actual wind speed and the projection relationship on the $X$ path, and Eq. (6) represents the correspondence between the measured projection and the measured wind speed.

Fig. 3Single-path wind velocity measurement model

The actual wind speed and the measured wind speed and wind direction are fitted to the data. Simply using the data to fit the relationship between $V$ and $U$ is not accurate enough, and the relationship between the two is more complex according with the variety of angle. The calculation of the wind direction will be more difficult. It will bring errors while using the general fitting function. The linear relationship was observed while $V_x$ and $U_x$ data at the same angle, it is worth to fit the polynomial relationship between $V_x$ and $U_x$:

Ghaemi-Nasab M. proposed a fitting scheme of $V$ and $U_x$ in the $D$/$L$= 20 orthogonal path wind model (Eq. (7)). In which the measurement bias of $U_x$ is derived from the deviation of the projection angle of $V$ on the path:

Obtained by Eq. (7) and (5):

Below is Ghaemi-Nasab M. according to the Eq. (7) by using the experimental data fitting the Ф third-order function in the form of expression:

2.3. Angle compensation method of wind and ultrasonic path

In the single-path experiment, as shown in Fig. 3, we cannot derive the values of $V$ and $\theta$ from $U$. In an commercial used two-dimensional wind gauge system, data on two paths is required to obtain complete wind speed information.

The experiment used the most common orthogonal dual path model as shown in Fig. 1. The wind speed and direction in the two-dimensional direction are calculated by measuring the data through two paths. Comparing the sizes of $t_x$, $t_{-y}$, $t_{-x}$, $t_y$ can determine which direction (quadrant) the wind is blowing. In the application, you can firstly determine the quadrant where the blow is located, and then calculate the angle $\theta$ between the wind and the $x$-axis. From anticlockwise, the wind direction is $\theta$ when blows from the first quardrant, the second quadrant blows the wind direction to 90° + $\theta$, the third quadrant blows the wind direction to 180° + $\theta$, and the fourth quadrant blows the wind direction to 270° + $\theta$.

$\theta$ is the actual angle between the wind and the path ($0\le \theta \le \pi /2$) ${\theta }_s$ is the measured angle between the wind and the path ($0\le {\theta }_s\le \pi /2$). $U_x$, $V_x$ and $U_y$, $V_y$ corresponding to the measured and actual wind speeds on the $X$-axis and $Y$-axis paths.

The actual wind speed on the two paths of the $x$-axis and the $y$-axis is derived from Eq. (8). The relationship between the actual wind speed and the measured wind speed is given by Eq. (10) and Eq. (11). Eq. (14) is the relation between ${\theta }_s$ and ${\theta }_o$.

$X$ axis:

$Y$ axis:

The $Y$ path is deduced from Eq. (9) as follows:

Obtained by Eqs. (11) and (10):

3.1. The fitting relation between the angle measurement data and the angle compensation method of wind and ultrasonic path

The ultrasonic measurement data of the ultrasonic wind meter was obtained at 13 angles of 9 wind speeds [6].

The relationship between the actual angle $\theta$ and the measured angle ${\theta }_s$ in the case of measuring nine wind speeds is shown in Fig. 4. The wind angles measured under different wind speeds at the same wind speed angle are basically coincident. The sum of squared residuals is 0.0049, this two fit well.

3.2. The difference between the angle measurement and the actual value after the algorithm compensation

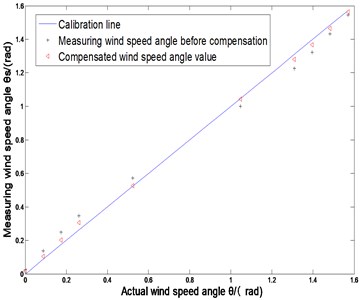
In fact, the actual projected wind speed on the path at the same angle is proportional to the measured wind speed deducted from Eq. (8). In Fig. 5, the measurement angle of the wind speed $V=$16.73 m/s is compensated, and the measurement error is found to be the largest when the angle between the wind speed angle and the sensor measurement path is between 5.73° and 22.9°. The compensation wind speed angle represented by “△” is closer to the actual calibration line than “+” which represents the measured value before compensation, and the compensated data has smaller error.

By calculation, the residual square sum $Q$ of the measured angle and the actual value before compensation is 0.0366, and the squared sum of the measured angle and the actual value after compensation is 0.0052.

Fig. 4Wind angle compensation function and measurement angle

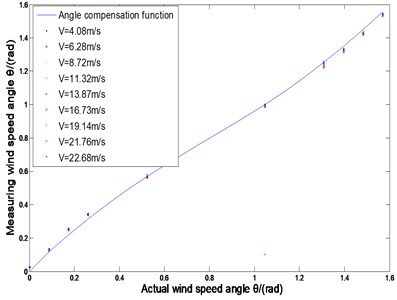
Fig. 5Comparison before and after measuring wind angle compensation

3.3. Error changes before and after wind speed compensation

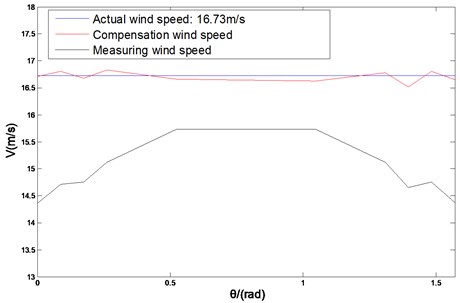
In Fig. 6, comparing the values of the wind speed U before and after compensation, the error caused by the shadow effect is significantly reduced. Among them, the measurement error of wind speed is 14.65 %, and the error after algorithm compensation is 1.74 %.

The squared sum $Q$ of the residual wind velocity U and the actual value before compensation is 34.4620. While after the compensation, the value is 0.0943.

Fig. 6Comparison before and after measurement of wind speed compensation

It is found that the sum of the squares of the residuals of the data after the algorithm compensation is reduced obviously. It indicates that the compensation value is well fitted to the actual measured value.