Analysis of gearshift processes in an automatic transmission at low vehicle speeds

1. Introduction

The basis of the vehicle automatic transmissions (AT) control system is a gearshift map. Usually the map is built in coordinates of the vehicle speed, determined by the speed sensor of the output shaft of the AT, and the percentage of opening the engine throttle (Fig. 1) [1-5].

Fig. 1A gearshift map of the 6-speed AT [1]

The solid lines 1-2, 2-3, 3-4, etc. on the shifting map are lines of shifting from lower to upper gears, and dashed lines 2-1, 3-2, etc. are lines of shifting from upper to lower gears. Solid lines are primarily determined by the technical characteristics of the engine (torque, rotation speed, fuel consumption) and the requirements of the driver. Throttle opening close to 100 % means that the vehicle speed needs to be maximized. The mid-throttle gearshift should be made to achieve some fuel economy with average acceleration. With a small throttle opening, gear shifting should provide the lowest fuel consumption. The dashed lines of reverse shifting are selected as a result of a compromise between the driving conditions, the requirements of the driver and the reserve of the engine torque.

As can be seen from Fig. 1, when the vehicle speed is less than 60 km/h, the shifting lines between adjacent gears are quite close. Periodic changes in the external conditions of the vehicle’s movement can lead to that the automatic gearshift control system will loop when driving at a constant speed in the zone of close values of the shifting speeds to adjacent gears. For example, such a regime can be observed on hilly roads, when moving downhill upshift occurs, and when moving uphill downshift occurs. An increase in the gearshift frequency leads to additional energy losses, an increase in fuel consumption, a reduction in the service life of the gearbox and a passenger discomfort [3, 4].

The purpose of the paper is to study and simulation the loop gear shifting process using a simplified dynamic model of the vehicle transmission. Modeling the process of gear shifting loop in order to predict the occurrence of this phenomenon and its prevention is important for creating adaptive automatic cruise-control systems, as well as automatic control systems for autonomous vehicles.

2. Dynamic model

The dynamic model of a vehicle with AT is based on an analysis of the connection diagram and the characteristics of its components. High-speed transmission elements include movable engine elements, a torque converter (or clutch), and a gearbox input shaft with a clutch and pinion gear engaged. Medium-speed elements are the output shaft of the gearbox with driven gears and the driveshaft with the drive gear of the differential. The low-speed elements of the transmission are the movable links of the differential and the axle shafts with drive wheels. The body mass reduced to the axles is $m=P/g$, where $P$ is the vehicle weight, depends on the slipping of the drive wheels on the road surface. Slip coefficient $\epsilon =V/\mathrm{\Omega }R$, where $V$ is the vehicle speed, $\mathrm{\Omega }$ is the angular rotation speed of the wheels; $R$ is the radius of the wheel. The coefficient $\epsilon$ depends on the road surface.

A simplified dynamic model of the vehicle’s 2-speed AT in accordance with the above description showed in Fig. 2.

Fig. 2A simplified dynamic model of the vehicle’s transmission with 2-speed gearbox

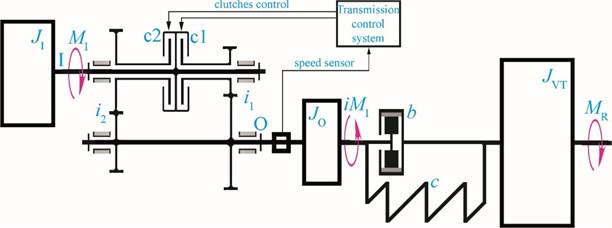
The dynamic model presented above is common [3, 5, 6] to any AT with discrete gear ratios, including planetary transmissions with a torque converter and dual-clutch transmissions with fixed axles of gear wheels.

We assume that the torque converter is blocked by a locking clutch and the engine output shaft is connected to the input shaft I of the gearbox for analyzing the dynamic processes of gear shifting in the AT. Therefore, the inertial element $J_I$ on the input shaft of the gearbox takes into account the moments of inertia of the moving parts of the engine and torque converter in the dynamic model. The most flexible element is the driveshaft after the output shaft O of the gearbox in the transmission. Its elastic and damping properties in a dynamic model can be represented as an elastic element (spring) with rigidity $c$ and damper $b$. Therefore, the inertial element $J_O$ characterizes the sum of the moments of inertia of the output shaft of the gearbox with the inertia moments of the gears of the gearbox and half the moment of inertia of the driveshaft. $J_{VT}$ is the second half of the moment of inertia of the driveshaft with the inertia moments of the subsequent transmission links and the vehicle body.

The gear shift duration in modern automatic transmissions is 0.2-0.5 sec [3, 5]. Such a short gear shifting time allows to consider this process as a collision. The inertial torques caused by a sharp change in the speeds of the transmission elements significantly exceed the engine torque and the reduced torque of the resistance force in this case. The aforesaid allows to attribute the considered model (Fig. 2) to vibration-impact systems [7] and, firstly, to consider the actual process of gear shifting in the gearbox using the impact theory and the theorem on the change in the angular momentum of a mechanical system upon impact [8], and, secondly, to determine the initial conditions for solving the differential equations of vehicle motion on the intervals between gear shifts.

The shift from first to second gear occurs when the acceleration is ${\dot{\omega }}_O>0$, and the shift from second to first gear occurs when ${\dot{\omega }}_O<0$. The impact interaction of the gearbox elements is accompanied by a rapid change in the kinematic relationships determined by the gear ratios. The greater the difference between the gear ratios, the greater the magnitude of the impact impulse. The input shaft I rotation speed of the gearbox is related to the rotation speed of the output shaft O with gear ratios: ${\omega }_I^{\left(12\right)}=i_1{\omega }^{\left(12\right)}$ when shifting from first gear to second, ${\omega }_I^{\left(21\right)}=i_2{\omega }^{\left(21\right)}$ when shifting from second gear to first (${\omega }^{\left(12\right)}$ and ${\omega }^{\left(21\right)}$ are rotation speed of the shaft O at which the gearshift occurs form first gear to the second and from second gear to the first correspondingly). $\left|i_1\right|>\left|i_2\right|$ the absolute values of the gear ratios from the input shaft I to the output shaft O are taken, since the rotation direction of the output shaft is not taken into account. The rotation speed of the element $J_I$ will decrease at shifting to second gear, and it will increase when shifting to first gear [8]. The rotation speed of the element $J_O$ before gear shift from the first gear to the second is ${\omega }^{\left(12\right)}$, and the rotation speed of the element $J_I$ at this moment is $i_1{\omega }^{\left(12\right)}$. The moment of inertia of the element $J_I$ reduced to the output shaft O before engaging the second gear is $J_I{i}_2^2$.

The theorem of angular momentum conservation upon impact for inertial elements $J_I$ and $J_O$ before and after the second gear is engaged:

where ${\omega }^{\left(2\right)}$ is the speed of the output shaft after the shift to second gear. Moreover, ${\omega }_I^{\left(2\right)}=i_1{\omega }^{\left(12\right)}$, then we get:

Similarly, the theorem of angular momentum conservation upon impact for inertial elements $J_{\mathrm{I}}$ and $J_O$ before and after the first gear is engaged:

where ${\omega }^{\left(1\right)}$ is the speed of the output shaft after the shift to first gear. Moreover, ${\omega }_I^{\left(1\right)}=i_2{\omega }^{\left(21\right)}$, then we get:

The total moment of inertia of the engine and gearbox elements $\left(J_{\mathrm{I}}{i}^2+J_O\right)$ before the link with maximum flexibility can be considered at intervals between gear shifting after reducing the moment of inertia $J_I$ to the output shaft. This eliminates one of the three degrees of freedom in the dynamic model (Fig. 2).

The movement of the model in the $i$-th gear ($i=1,2$) between the gear shifts is described by a system of two linear differential equations:

In Eq. (1), the superscript in parentheses indicates the number of the gear engaged; $\phi$ is the angular coordinate of the inertial element $\left(J_{\mathrm{I}}{i}^2+J_O\right)$; ${\phi }_{VT}$ is the angular coordinate of the inertial element $J_{VT}$.

Free vibration frequencies of the model in the absence of damping: $k_1=0\text{;}$$k_2^{\left(i\right)}=\sqrt{c\left(J_{\mathrm{I}}{i}^2+J_O+J_{VT}\right)/\left(J_{\mathrm{I}}{i}^2+J_O\right)J_{VT}}\text{.}$ Frequency of damped oscillations: ${k_2^{*}}^{\left(i\right)}=\sqrt{{k_2^{\left(i\right)}}^2-{h^{\left(i\right)}}^2}$, where $h^{\left(i\right)}=b\left(J_{\mathrm{I}}{i}^2+J_O+J_{VT}\right)/2\left(J_{\mathrm{I}}{i}^2+J_O\right)J_{VT}$.

3. Model movements between gear shifts

The movement of the model between gear shifts is a torsional vibration of inertial elements $\left(J_{\mathrm{I}}{i}^2+J_O\right)$ and $J_{VT}$ relative to the center of mass, rotating under the action of the engine torque and the moments of resistance forces $M_I=const\ne 0$, $M_R=const\ne 0$. The center of mass motion of the model is the absolute model movement. The relative motion of the elements $\left(J_I{i}^2+J_O\right)$ and $J_{VT}$ are their synchronous torsional vibrations in antiphase, and the magnitudes of the oscillation amplitudes are inversely proportional to the moments of inertia [9]. The general solution of the obtained Eq. (1) has the form:

where ${\mu }^{\left(i\right)}=A_{VT}^{\left(i\right)}/A^{\left(i\right)}=-\left[(J_I{i}^2+J_O)/J_{VT}\right]$, $a^{\left(i\right)}=\left(i{M}_I{-M}_R\right)/\left(J_I{i}^2+J_O+J_{VT}\right).$

The constants $A$, $\beta$, $C_1$ and $C_2$ are determined through the initial conditions, that is, through the initial angular coordinates and velocities of the inertial elements of the model. In Eq. (2), parameters $C_1$, $C_2$ and $a$ are the characteristics of the absolute motion, i.e., the mass center motion of the model, parameters $A$ and $\beta$ are the characteristics of the relative motion.

By differentiating Eq. (2), we obtain a general form of the equations of mass velocities in the $i$-th gear ($i=1,2$) between the gear shifts:

The absolute speed $C_2^{\left(i\right)}$ is the initial center of mass velocity of the model in the $i$th gear. Substituting $\sin {\alpha }^{\left(i\right)}=h^{\left(i\right)}/\sqrt{{h^{\left(i\right)}}^2+{{k_2^{*}}^{\left(i\right)}}^2}$ and $\cos {\alpha }^{\left(i\right)}={k_2^{*}}^{\left(i\right)}/\sqrt{{h^{\left(i\right)}}^2+{{k_2^{*}}^{\left(i\right)}}^2}$ expressions of mass velocities are transformed to the form:

The motion modes of a transmission model are determined by gear shift speeds. The gear shift from first to second gear will take place when ${\omega }^{\left(1\right)}={\omega }^{\left(12\right)}$ and ${\dot{\omega }}^{\left(1\right)}>0$; the gear shift from second gear to first when ${\omega }^{\left(2\right)}={\omega }^{\left(21\right)}$ and ${\dot{\omega }}^{\left(2\right)}<0$.

The angular coordinate Eq. (2) and the velocity function ${\omega }_{VT}$ are continuous over the entire interval of motion, and the continuous velocity function $\omega$ at intervals is a discontinuous function with finite jumps between intervals. The last circumstance is a sign of the nonlinearity of the system under consideration, for solving the dynamics of which we apply the stitching method.

The conditions for stitching coordinates and speeds of the model at adjacent intervals when shifting from first gear to second are:

where $t_k^{\left(i\right)}$ is the time period between gear shifts.

The angular coordinates and velocities of the model elements before the first shift from the first gear to the second should be given or known if the model’s movement in the first gear is somehow specified: Eqs. (2) and (3).

The initial values of the angular coordinates and velocities of the model elements in second gear obtained from stitching conditions Eq. (4) determine the constants $A^{\left(2\right)}$, ${\beta }^{\left(2\right)}$, $C_1^{\left(2\right)}$ and $C_2^{\left(2\right)}$ for solutions of the differential equations of the model motion in second gear:

Fig. 3The graph of the changing the angular velocity at variable acceleration

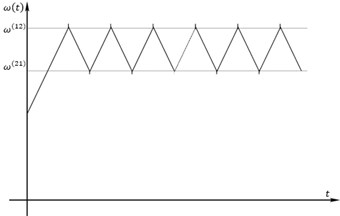
The general algorithm for calculating constants on the intervals of continuous movements according to known initial conditions includes the following steps:

1) Subtraction of the left and right parts of the second equation of the system Eq. (5) from similar parts of the first equation: ${\phi }^{\left(2\right)}\left(0\right)-{{\phi }_{VT}}^{\left(2\right)}\left(0\right)=\left(1-{\mu }^{\left(2\right)}\right)A^{\left(2\right)}\mathrm{s}\mathrm{i}\mathrm{n}{\beta }^{\left(2\right)}.$

2) A similar action with the fourth and third equations of system Eq. (5) and the following identical permutations:

3) Multiplication of the right and left sides of the third equation of system Eq. (5) by $\mu$ and the subsequent subtraction from the fourth equation of the third: ${{\omega }_{VT}}^{\left(2\right)}\left(0\right)-{\mu }^{\left(2\right)}{\omega }^{\left(2\right)}\left(0\right)=\left(1-{\mu }^{\left(2\right)}\right){C_2}^{\left(2\right)}.$

The first two equations allow to determine $A^{\left(2\right)}$ and ${\beta }^{\left(2\right)}$, the last equation allows to determine ${C_2}^{\left(2\right)}$. The constant ${C_1}^{\left(2\right)}$ in the first interval of the model motion can be accepted equal to zero, and at subsequent intervals it is equal to the sum of the displacements of the model center of mass at previous intervals.

The movement of the model in second gear, described by Eqs. (2) and (3), ends at time $t_k^{\left(2\right)}$, when the conditions ${\omega }^{\left(2\right)}\left(t_k^{\left(2\right)}\right)={\omega }^{\left(21\right)}$ and ${\dot{\omega }}^{\left(2\right)}\left(t_k^{\left(2\right)}\right)<0$ will be met. This is an important point for solving the issue of the existence of the effect of a gear shift loop.

4. Numerical simulation

A numerical simulation of the model motion carried out using the obtained dependences. The graph of the changing the angular velocity at variable acceleration is shown in Fig. 3.

5. Conclusions

A mathematical model is developed to simulate the processes of gear shift loop caused by the vehicle moving at a constant low speed along a hilly (or winding) section of the road. The model contains elastic and dissipative elements, a control system that generates gear shifting commands in accordance with the output shaft rotation speed sensor.

Relations are derived for determining the coordinates and speeds of transmission elements before and after gear shifts. A numerical simulation of gear shifting processes was performed, the possibility of gear shift loops was showed. The most effective way to eliminate unwanted gear shifting loop is to use navigation maps that take into account the topography of the road [10]. In addition, an effective method is to extend the boundaries of gear shifts on the gear shift map in the case of diagnosing loops [11].

The obtained mathematical model allows for any vehicle motion determine the conditions for the occurrence of loop gear shifts and develop measures to eliminate this phenomenon. The model can also be used in the development of automatic transmission gear shift control systems and for calibration the engine and transmission at various operating modes and traffic conditions.