Damage detection in sluice hoist beams subject to excitation at resonance frequency band based on local primary frequency

1. Introduction

In the long-term service of the sluice, cracks occur inevitably in hoist beams arising from the load and the aging of the material. The expansion and collection of cracks cut down the normal working performance of hoist beams and destroy the safety of the sluice structural system [1, 2]. Traditionally, the detection of sluice hoist beams cracks relies on artificial visual inspection method, but this method is subjective and inaccurate [3, 4]. Damage detection method based on the change of natural frequency is a new method for detecting cracks of sluice hoist beams [5, 6]. This method is effective when the damage extent is large, but exhibits insensitivity about local damage in minor damage extent [7]. Since sluice structural system is complex and large in scale, the local damage of the hoist beams has a limited influence on global structural frequency of the sluice [8].

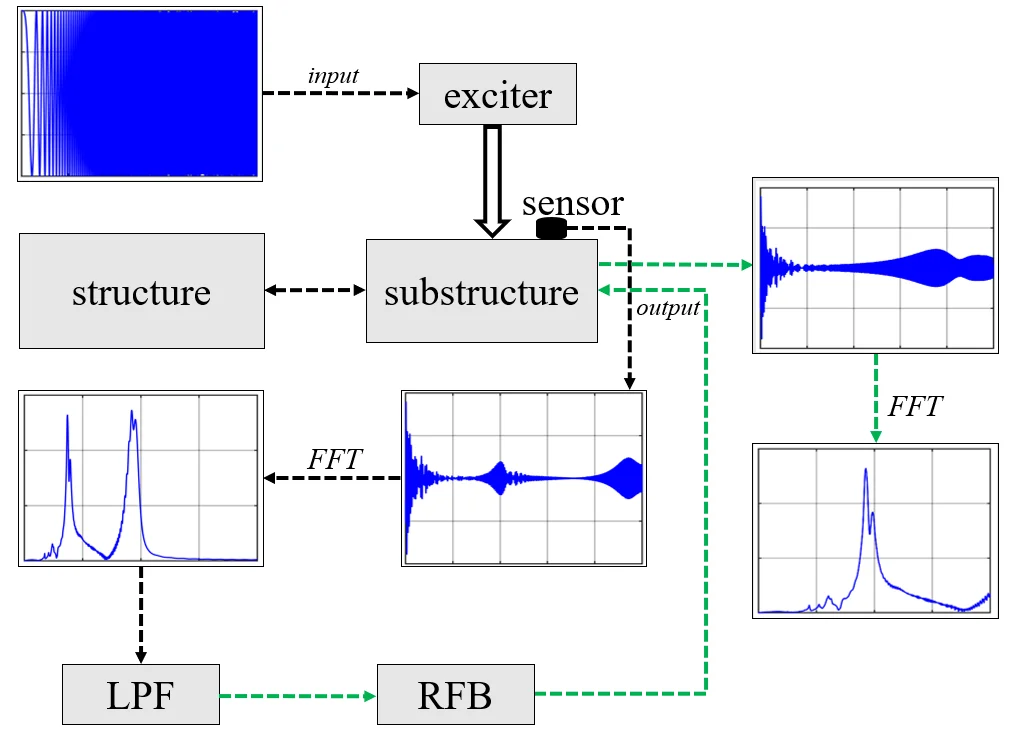
In order to overcome the defect of method based on frequency, the local primary frequency (LPF) in the local mode is provided to identify the minor damage of sluice hoist beams. Local mode is defined as a special mode of the vibration mode set of a complex structural system composed of multiple substructures. Local mode is dominated by the vibration of a certain substructure, while other substructures are approximately stationary. In local mode, the certain substructure carries nearly all the vibration energy and embodies the vibration effect. Hou et al. defined the natural frequency of the structure in local mode as the LPF of the substructure [9]. LPF eliminates the interference of other substructures and improves frequency sensitivity about the local damage.

In this paper, the proposed resonance frequency band (RFB) excitation is combined to maximize the local mode. The change ratio of LPF is utilized to detect damage of sluice hoist beams. The validity of this method is verified by numerical experiments. Damage identification of a hoist beam under different number and degree of cracks is carried out.

2. Damage detection method based on LPF driven by RFB

Assume an $n$ degree of freedom system with $m$ substructures, Hou et al. indicated the sensitivity ${\xi }_{r,i}$ of $r$th order natural frequency about the damage of substructure $i$ can be expressed as [9]:

where ${\phi }_{i,r}$ is the mode shape of substructure $i$, $K_i$ is the local stiffness matrix of substructure $i$, and ${\omega }_r$ is the $r$th order frequency of system.

The $r$th order frequency is the LPF expressed as ${\omega }_{LPF}$ about substructure $i^{\mathrm{*}}$ when there is a local mode with only one substructure $i^{\mathrm{*}}$ vibration. The mode shapes of the other substructures are almost zero, so the sensitivities of ${\omega }_{LPF}$ about damage of other substructures are also almost zero, hence the damage of other substructures cannot be reflected on ${\omega }_{LPF}$. However, the damage of substructure $i^{\mathrm{*}}$ affects ${\omega }_{LPF}$, and the stronger the vibration of the substructure $i^{\mathrm{*}}$, the larger the mode shape of the substructure $i^{\mathrm{*}}$ position, the sensitivity ${\xi }_{LPF,i^{\mathrm{*}}}$ about the damage of substructure $i^{\mathrm{*}}$ is also higher.

The key to obtain the LPF is to make the substructure we focused full vibration while other substructures should stay stationary. In structural dynamics, the vibration response is weak when excitation frequency $\omega$ is far from ${\omega }_{LPF}$; The vibration response is the strongest when $\omega$ is equal to ${\omega }_{LPF}$; When $\omega$ is located in the interval near ${\omega }_{LPF}$, the response of is also sufficient although the vibration response does not reach the maximum. Here, the interval is defined as RFB which can be expressed as:

where $\beta$ is the ratio of $\omega$ and ${\omega }_{LPF}$, ${\beta }_1$ and ${\beta }_2$ are the lower and upper limits of the RFB.

According to the theory of structural dynamics, the amplification factor $\lambda$ of displacement response with respect to the excitation frequency is:

where $\zeta$ is the damping ratio, generally determined based on experience or field testing.

The establishment of the RFB requires consideration of damping characteristic of structure and selection of appropriate amplification factor. In this study, the damping ratio of the sluice is taken as 0.02, the amplification factor is taken as 4, ${\beta }_1=$0.866 and ${\beta }_2=$1.118 are calculated.

Damage reduce structural stiffness and change frequency compared to healthy structure [10, 11]. Define the change ratio of LPF as the damage identification index:

where ${\omega }_{LPF}$ is LPF of sluice hoist beam in healthy condition, ${\omega }_{id}$ is LPF of sluice hoist beam identified from the dynamic responses.

3. Numerical verification

3.1. Finite element model of the sluice structural system

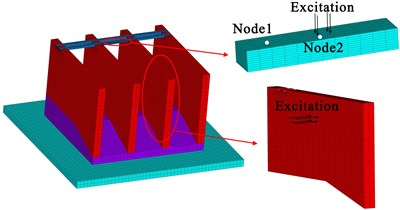
The finite element model of a sluice is established as shown in Fig. 1. The model composed by 38,131 nodes and 36,548 elements is divided into four parts: foundation, bottom plate, gate pier and hoist beam.

Fig. 1Model of the sluice structural system

3.2. Results and discussions

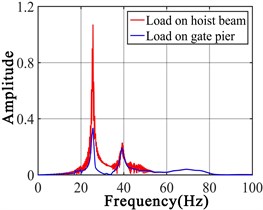
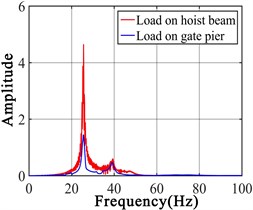
Sweep frequency excitation (SFE) is applied to the gate pier and the hoist beam, respectively. The acceleration responses of node 1 and node 2 are extracted to perform FFT, the results are shown in Fig. 2.

Fig. 2Frequency domain responses forced by SFE: a) node 1, b) node 2

a)

b)

Two peaks exist on the spectrogram when the excitation is applied to gate pier, but LPF is hard to be chosen. However, the LPF located near 25 Hz can be clearly identified when the excitation is applied to the hoist beam. The LPF obtained by node 2 is significantly larger than the LPF obtained by node 1. Since node 2 is located at the middle of the hoist beam but node 1 is located at the side of the hoist beam, the vibration displacement of the node 2 is larger than the vibration displacement of the node 1. During the process of damage detection, excitation can be directly applied to the substructure we focused, and sensors can be placed in position where the vibration displacement is large, so the LPF can be obtained more easily.

LPF of the hoist beam is identified as 25.63 Hz and the RFB calculated from 2.2 is between 22.20 Hz and 28.65 Hz. The responses of node1 and node2 forced by SFE and RFB are shown in Fig. 3.

Fig. 3(a, c) display the LPF amplitude identified by the RFB is approximately twice of the amplitude of the LPF identified by SFE. The RFB causes the amplitude of the LPF to be further amplified, so that the noise robustness of the LPF is enhanced. Fig. 3(b, d) show RFB makes the structural vibration more intense, and increases the sensitivity of the LPF about substructure damage, so the influence of minor damage on the LPF is improved.

Fig. 3Responses forced by RFB and SFE a) frequency domain responses of node 1, b) time domain responses of node 1, c) frequency domain responses of node 2, d) time domain responses of node 2

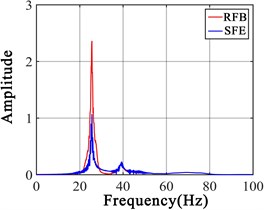
a)

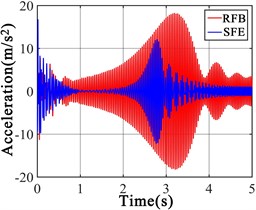
b)

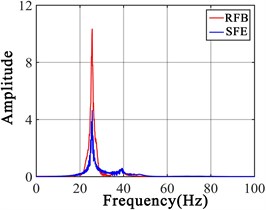
c)

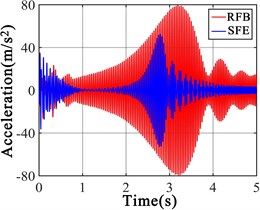
d)

Assume that the damage extent of hoist beam is linear with the number and the extent of cracks, and the damage extent is defined as $\gamma =ij/30$. For the convenience of description, $dij$$(i=1,\mathrm{2,3}$; $j=\mathrm{1,2},\dots ,10)$ is used to represent the damage situation, where $i$ is the number of cracks and $j$ is the extent of cracks. SFE and RFB are applied to the hoist beam of different damage extent, the acceleration responses of node 2 are extracted. The damage identification results identified by FCR are shown in Fig. 4-6.

Fig. 4Damage identification results of three cracks

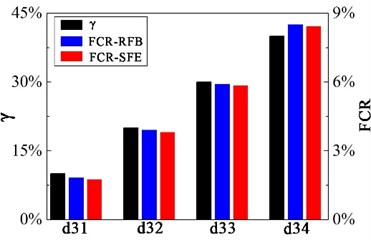
When three cracks exist in the hoist beam, both excitations have satisfactory damage identification effects. The damage extent of the three cracks is large, the change ratio of the LPF is easy to be obtained, so the advantage of the RFB is not obvious.

The SFE cannot play a role in small damage situations when two cracks exist in the hoist beam. As the extent of damage increases, damage extent identified by the RFB is closer to the actual damage.

Damage extent is relatively small when one crack exists, the frequency change cannot be perceived from acceleration responses forced by SFE when $j=$1, 2. However, the FCR can be obtained under the action of the RFB, the damage extent identified is slightly smaller than the actual damage extent. When $j=$3, 4 damage extent can be identified by SFE, but the error is greater than the damage extent identified by the RFB.

Fig. 5Damage identification results of two cracks

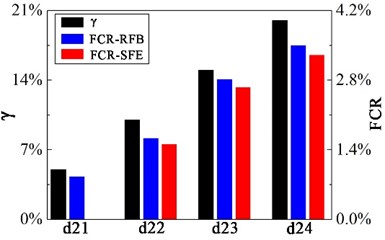
Fig. 6Damage identification results of one crack

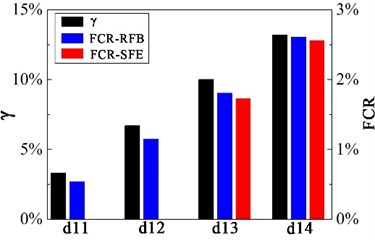
The above results show RFB has obvious advantages for discovering the minor damage of hoist beam, and the identification effect is good under different damage extents.

4. Conclusions

This paper presents a method for detecting damage in sluice hoist beams. Numerical simulation is carried out to verify that the change of the LPF can effectively identify the damage extent of the sluice hoist beam forced by the RFB, conclusions can be obtained as follows:

1) The LPF mainly related to the dynamic characteristics of the substructure has high damage sensitivity about the substructure. In actual detection, excitation can be directly applied to the substructure we focused to excite the local mode fully in order to obtain the LPF.

2) The RFB excitation increases the sensitivity of the LPF about the substructure damage, and amplifies the influence of local minor damage on frequency.

3) Damage extent of the hoist beam is evaluated by the change ratio of LPF. The damage identification is effective under different cracks number and depth. This method can provide a basis for the preliminary detection of the sluice hoist beam damage in actual engineering.