Measurement of damping properties of beeswax and cosmetic wax using Oberst beam method

2.1. Bare beam (Undamped)

Damping loss factor for a uniform beam of length $l$, thickens $H$ with density $\rho$ can be calculated by following expression, as specified in ASTM E756-93 standard [1]:

where, $f_n$ is resonance frequency of mode $n$ and $\mathrm{\Delta }{f}_n$ is half power bandwidth. Expression of Young’s modulus for bare beam as specified in ASTM E756-93 standard [1] is given by:

where, $C_n$ is coefficient for mode $n$ of the cantilever beam, $E$ is Young’s modulus of bare beam.

2.2. Beam with damping layer on a single side

In case of the composite beam (damping layer on a single side), expressions for Young’s modulus and loss factor specified in ASTM E756-93 standard are based on Ross-Kerwin-Ungar (RKU) equation [4]:

where, $E_1$ is Young’s modulus of damping material (MPa), $M=E_1/E$ is Young’s modulus ratio. $H$ is thickness of bare beam (m), $H_1$ is thickness of damping material (m), $T=H_1/H$, thickness ratio. $\rho$ is density of bare beam (kg/m³), ${\rho }_1$ is density of damping material (kg/m³), $D={\rho }_1/\rho$ density ratio. $\alpha ={\left(f_c/f_n\right)}^2\left(1+DT\right)$ and $\beta =4+6T+4T^2$. $\eta$ is loss factor of bare beam, ${\eta }_1$is loss factor of damping material, ${\eta }_c=\mathrm{\Delta }{f}_c/f_c$, loss factor of composite beam (bare beam and damping material), $\mathrm{\Delta }{f}_c$ is half power bandwidth for modes of composite beam (Hz), $f_c$ is resonance frequency for mode $n$ of composite beam (Hz), $f_n$ is resonance frequency for mode $n$ of bare beam (Hz). $l$ is length of bare beam (m), $I$ is moment of inertia of bare beam (m⁴), $A$ is area of bare beam (m²).

3.1. Test samples details

In the current study, two bare samples of mild steel material with 7900 kg/m³ density with dimensions of 240 mm×20 mm×1.7 mm and 240 mm×20 mm×2 mm (length×width×thickness) are considered. Here, different thicknesses of bare samples are chosen to study effect of bare sample thickness on damping. Fig. 1 shows schematic of bare sample and with damping material as a layer. The root is a sample holding mechanism in Oberst beam method.

Fig. 1Schematic of test samples: a) bare sample, b) bare sample with damping layer

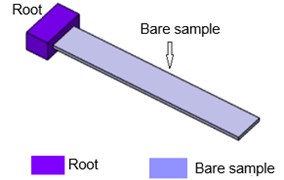
a)

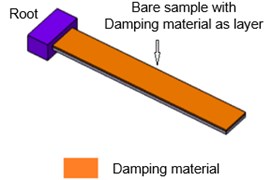
b)

Natural wax is prepared by crushing honey bee hives (without honey) and then heated until it becomes a soft gel. It is applied to bare samples as a layer and curing is done at room temperature about 14 hours. For cosmetic wax (i.e. bleached wax which is available in the market), it is heated between 5to 10^o C of above room temperature in wax heater and then applied to bare sample as a layer. The densities of these wax materials are calculated based on the measurement of weight by a volume ratio at room temperature and corresponding values are reported in Table 1. It also presents the details about test samples and damping materials. In present research, total eight test samples are studied (excluding bare samples) in damping test with a different combination of damping material (beeswax and cosmetic wax) and bare sample thickness. Details regarding these eight test sample’s notation are shown in Table 2.

Table 3 shows parametric study to understand variation in damping property’s measurement with respect to damping materials, damping material thickness and bare sample thickness.

3.2. Oberst beam method (OBM)

Experimental test setup for Oberst beam is shown in Fig. 2(a). In this method, non-contact type magnetic force transducer (placed at a free end of the beam) and capacitive displacement transducer (placed near the clamped condition) are used. Input excitation to test sample is provided by force transducer, the response is measured by capacitive displacement transducer and is expressed in terms of Frequency Response Function (FRF). To avoid adverse effects of noncontact electromagnetic excitation, appropriate position of force and displacement transducer are obtained from different trial measurements [8]. Necessary precautions are considered as per ASTM [1] standard during measurements. Here, a random signal is used as an input excitation and natural frequencies are measured based on the measured FRF by locating peaks. Damping properties are obtained using half-power method by locating the 3 dB reduction from peak amplitude of FRF.

Repeatability study of ten measurement trials has been conducted on 1.7 mm bare sample to verify consistency in ten measurements and corresponding results are shown in Fig. 2(b). It can be observed that there is good repeatability from all ten measurements.

Fig. 2a) Experimental setup for Oberst beam method (OBM), b) frequency response functions for different test trials measured using Oberst beam method

a)

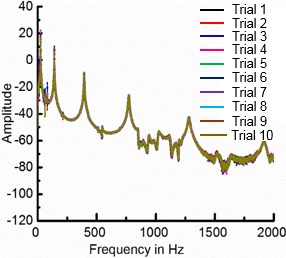
b)

4.1. Damping measurement of composite beam

Damping loss factor for composite beam (bare beam + damping material) of all eight samples (A to H) is measured using half-power bandwidth method. Cosmetic wax and beeswax composite loss factor are shown in Figs. 3(a) and (b), respectively. It can be observed that composite loss factor is increasing with respect to damping material thickness as well as bare beam thickness. This is due to more flexure in damping material. The deflection is more as damping layer is away from the neutral axis.

Fig. 3Composite loss factor with respect to frequency: a) Cosmetic wax, b) Beeswax

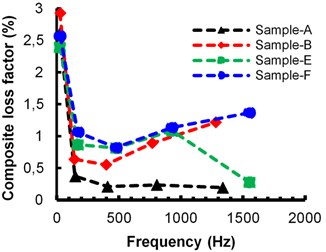
a)

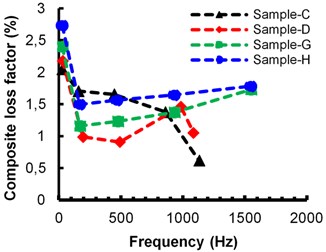
b)

4.2. Cosmetic wax v/s Beeswax

To identify best damping material having higher loss factor out of cosmetic wax and beeswax, for bare beam thickness 1.7 mm samples B, D and for bare beam thickness of 2 mm samples F, H are considered for the study. These test samples consist of equivalent damping material thickness (2.53 mm) and same testing method is used. A comparison of measured cosmetic and beeswax properties are shown in Fig. 4. It is observed that cosmetic wax has higher loss factor compared to beeswax and is shown in Fig. 4(a) and (b).

Fig. 4Comparison of measured beeswax and cosmetic wax damping loss factor: a) 1.7 mm bare beam thickness, b) 2 mm bare beam thickness

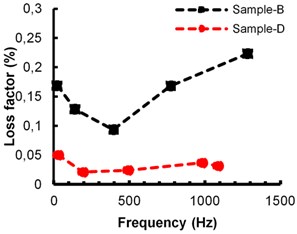
a)

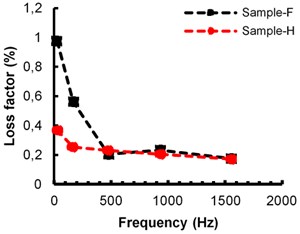
b)

4.3. Effect of damping material thicknesses and effect of bare sample on loss factor

To understand the effect of damping material thickness on loss factor the following samples are considered. Cosmetic wax samples with 1.7 mm bare beam thickness of A (1.29 mm damping material), B (2.53 mm damping material) and 2 mm bare beam thickness of E (1.29 mm damping material), F (2.53 mm damping material). Beeswax samples with 1.7 mm bare beam thickness of C (1.29 mm damping material), D (2.53 mm damping material) and 2 mm bare beam thickness of G (1.29 mm damping material), H (2.53 mm damping material). These sample result plots are shown in Fig. 5. Based on this study, it is observed that loss factor of damping material increases with increasing thickness of cosmetic wax and beeswax as shown in Fig. 5(a) and (b), respectively.

Beeswax samples of D (1.7 mm bare beam) and H (2 mm bare beam) and Cosmetic wax samples of B (1.7 mm bare beam), F (2 mm bare beam) are considered to understand the effect of bare sample thickness on material loss factor and corresponding results are shown in Fig. 5(a, b). For both the damping materials, damping thickness of 2.53 mm is considered. It can be observed from Fig. 5 that if thickness of bare sample increases then loss factor of damping material also increases without changing damping material thickness. The flexure deflection of damping layer increases as outer layer distance also increases from neutral axis for thicker bare beams.

Fig. 5Effect on loss factor due to thickness of damping material: a) cosmetic wax, b) beeswax

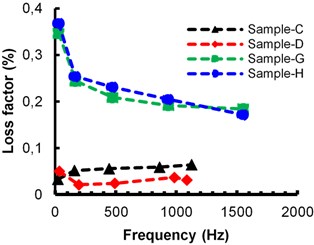
a)

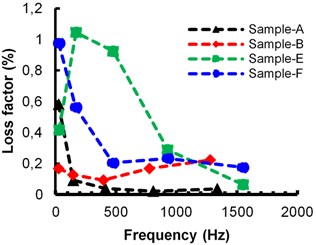
b)