Effect of in-wheel motor suspension system on electric vehicle ride comfort

1. Introduction

In recent years, in order to reduce environmental pollutions, electric vehicles have been studied and developed by researchers to improve the vehicle efficiency and they also pay much attention to perfecting the design to improve the ride quality. Yechen Qin et al. proposed a new approach for vibration mitigation based on a dynamic vibration absorbing structure (DVAS) for electric vehicles (EVs) using a model of the coupled longitudinal-vertical dynamics [1]. Abu Bakar S. A. et al. presented a simulation study on the ride comfort performance of a passenger vehicle which is expected to be converted into an electric vehicle using a validated 7 degrees of freedom of vehicle ride comfort model of the passenger vehicle [2]. Liqiang Jin et al. analyzed the influence of the ratio between unsprung and sprung mass on ride comfort of vehicles driven by in-wheel motors using an 11 degrees of freedom of vehicle ride comfort model [3].

To improve the electric vehicle ride comfort, the optimization, control, and optimal control methods are used to control EV suspension system. Abdussalam Ali A. O. and Başar Özkan analyzed the effect of in-wheel electric motors mass on the performance of passive and active suspension systems [4]. A modified GPSO-LQG controller is proposed by Fangwu Ma et al. for one-quarter EV suspension with the purpose of optimizing suspension performance for entire speed ranges [5]. Liu M. et al. proposed the ride comfort optimization of In-Wheel-Motor EV with In-Wheel vibration absorbers using two control methods such as the linear quadratic regulator (LQR) algorithm for suspension damper and the fuzzy PID method for in-wheel damper [6]. Ma Y. et al. proposed a new electric wheel with active control of suspension using LQG control theory for in-wheel motor [7]. Di Tan et al. proposed a dual-loop proportion integration differentiation controller based on the particle swarm algorithm is designed to control the active suspension of the EV driven by in-wheel motor [8].

The EV dynamic models are applied to study vehicle suspension and in-wheel electric motor suspension such as the quarter EV dynamic model [1, 7, 9], the half EV dynamic model [10] and the full vehicle [2, 3]. Vibration sources are considered excitation inputs for the EV dynamic models such as road surface [2, 3], in-wheel electric motor as well as the association of both excitation sources [9].

The major goal of this study is to establish a dynamic model of quarter vehicle with the combination of IWM vertical exciting force and road surface roughness excitations to analyze the effect of IWM suspension system on EV ride comfort. The $a_{wbz}$ value according to the international standard ISO 2631-1 (1997) [11] is selected as an objective function to analyze the effect of IWM suspension system when the road surface and IWM mass conditions change.

2. Electric vehicle dynamic model

2.1. One-quarter EV dynamic model

A one-quarter EV dynamic model without IWM suspension system and with IWM suspension system were established for analyzing the effect of IWM suspension system on EV ride comfort, as shown in Fig. 1.

Fig. 1One-quarter electric vehicle dynamic model

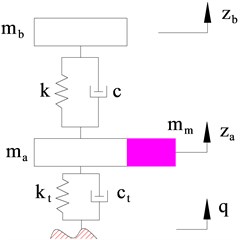
a) Without IWM suspension system

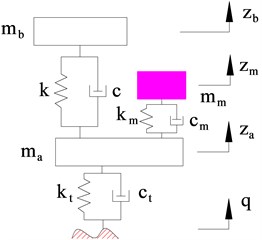
b) With IWM suspension system

In Fig. 1, $m_b$, $m_m$ and $m_a$ are the sprung mass of EV body, IWM mass, and EV unsprung mass respectively; $k_t$ and $c_t$ are the stiffness and damping coefficients of the tire; $k$and $c$ are the stiffness and damping coefficients of the EV suspension system; $k_m$ and $c_m$ are the IWM suspension system; $z_a$, $z_b$ and $z_m$ are the vertical displacements of the axles, vehicle body and IWM mass, respectively; $q$ is road surface excitation

Equations of motion: From the EV dynamic model as shown in Fig. 1(b), the dynamic equation of the quarter vehicle using Newton’s second law are written as follows:

1

$m_b{\ddot{z}}_b=-\left[k\left({\mathrm{z}}_b-z_a\right)+c\left({\dot{\mathrm{z}}}_b-{\dot{z}}_a\right)\right],$

2

$m_m{\ddot{z}}_m=F_{mz0}-\left[k_m\left({\mathrm{z}}_m-z_a\right)+c_m\left({\dot{\mathrm{z}}}_m-{\dot{z}}_a\right)\right],$

3

$m_a{\ddot{z}}_a=\left[k({\mathrm{z}}_b-z_a)+c({\dot{\mathrm{z}}}_b-{\dot{z}}_a)\right]+\left[k_m({\mathrm{z}}_m-z_a)+c_m({\dot{\mathrm{z}}}_m-{\dot{z}}_a)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_t\left({\mathrm{z}}_a-q\right)+c_t\left({\dot{\mathrm{z}}}_a-\dot{q}\right)\right],$

where, $F_{mz0}$ is IWM vertical exciting force.

3. Results and discussion

The differential equations of the quarter vehicle in Section 2 are solved based on the MATLAB/Simulink with a set of parameters of EV by the references [15]. When vehicle moves on the ISO road surface class B (according to the International Standards Organization CISO 8608 [14]) at vehicle speed $v$ = 50 km/h and IWM vertical exciting force $F_{mz0}=1500\mathrm{c}\mathrm{o}\mathrm{s}\left(1000t\right)/N$ at two cases such as with IWM suspension system in comparison without IWM suspension system (Case 1) and with IWM vertical exciting force in comparison without IWM vertical exciting force (Case 2), the simulation result of the time domain responses of the vehicle body vertical acceleration is shown in Fig. 2.

From the results of Fig. 2(a), we could determine that according to the international standard ISO 2631-1 the values of the weighted root-mean-square (r.m.s.) acceleration of the vertical vehicle body ($a_{wbz}$) are 0.417 m/s² without IWM suspension system and 0.381 m/s² with IWM suspension system, respectively with case 1. The IWM suspension system makes the value of $a_{wbz}$ reduce by 8.6 % in comparison without IWM suspension system which means that the effect of IWM suspension system on the vehicle ride quality is significant. Similarly, from the results of Fig. 2(b), $a_{wbz}$ the value 0.381 m/s² with IWM vertical exciting force and 0.369 m/s² without IWM vertical exciting force. The IWM vertical exciting force makes the value of $a_{wbz}$ increase by 2.2 % in comparison without IWM vertical exciting force.

Comparing with the IWM suspension system and without IWM suspension system when vehicle moves under the different operating conditions: the $a_{wbz}$ value for five different road surface conditions including ISO road surface class A, ISO road surface class B, ISO road surface class C, ISO road surface class D and ISO road surface class E were analyzed when vehicle moves at vehicle speed $v=$50 km/h and IWM vertical exciting force $F_{mz0}=1500\mathrm{c}\mathrm{o}\mathrm{s}\left(1000\pi t\right)/N$. The $a_{wbz}$ value with the IWM suspension system in comparison without IWM suspension system for five different road surface conditions is shown in Fig. 3.

Fig. 2The vehicle body accelerations with two cases

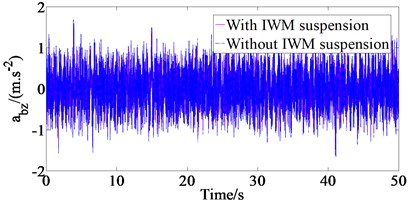
a) Case 1

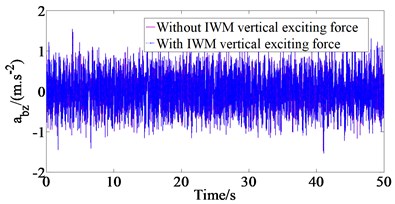
b) Case 2

From the results of Fig. 3, the values of $a_{wbz}$with IWM suspension system are indicated to reduce by 8.6 %, 8.6 %, 8.5 %, 8.5 % and 8.4 % in comparison to without IWM suspension system when the vehicle moves on changing bad road conditions. This means that the IWM suspension system has significantly improved the EV ride quality.

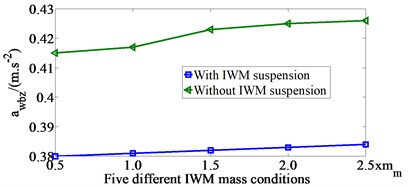
Comparing with the IWM suspension system and without IWM suspension system when the IWM mass condition changes: the $a_{wbz}$ value for five different IWM mass conditions were analyzed when vehicle moves on ISO road surface class B at vehicle speed $v=$50 km/h and IWM vertical exciting force $F_{mz0}=1500\mathrm{c}\mathrm{o}\mathrm{s}\left(1000\pi t\right)/N$. The $a_{wbz}$ value with the IWM suspension system in comparison to without IWM suspension system for five different IWM mass road surface conditions is shown in Fig. 4. From the results of Fig. 4, the values of $a_{wbz}$with IWM suspension system are indicated to reduce by 8.4 %, 8.6 %, 9.7 %, 9.9 % and 9.9 % in comparison to without IWM suspension system when the value of the IWM mass increases. The EV ride quality with the IWM suspension system is significantly improved for the cases of great IWM mass values.

Fig. 3The awbz value for five different road surface conditions

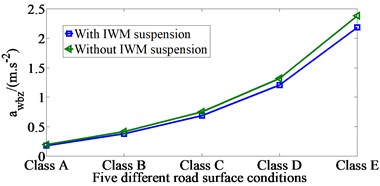
Fig. 4The awbz value for five different IWM mass conditions

4. Conclusions

In this study, a one-quarter EV dynamic model is developed for analyzing the effect of in- IWM suspension system on (EV) ride comfort. The major conclusions drawn from the analysis can be summarized as follows:

1) The value of $a_{wbz}$ with IWM suspension system reduces by 8.6 % in comparison to without IWM suspension system which means that the effect of IWM suspension system on the EV ride quality is significant;

2) The values of $a_{wbz}$ with IWM suspension system reduce by 8.6 %, 8.6 %, 8.5 %, 8.5 % and 8.4 % in comparison to without IWM suspension system when the vehicle moves on changing bad road conditions;

3) The values of $a_{wbz}$ with IWM suspension system reduce by 8.4 %, 8.6 %, 9.7 %, 9.9 % and 9.9 % compared with that without IWM suspension system, when the value of the IWM mass increases.