Kinematics analysis on pneumatic flexible finger

1. Introduction

At present, the common driving form of manipulator mainly includes motor drive, fluid drive and other forms [1]. Electric driven has the advantages of high precision and easy to control, but it has the disadvantages of large volume and poor flexibility [2]. The biggest advantage of hydraulic driven is large thrust, but it has the disadvantages of high cost, poor reliability and easy leakage [3]. In order to overcome the shortcomings of rigid manipulators and combine with the research status and trend of the flexible pneumatic actuator, a flexible finger is designed by using the multi-directional bending joint and unidirectional bending joint. The finger can bend like the human finger and can independently and coordinately control the bending angle of each joint. It has good flexibility and simple structure and can be used in agriculture, picking robot, service robot and other fields.

2. Structure and function of flexible joint

The finger is composed of two joints in series, which is shown in Fig. 1. The base joint is a multi-directional bending joint [4], with an effective deformation length of 50 mm. It is made up of four artificial muscles in parallel. The combination of ventilation of different muscles can realize multi-directional bending and axial extension of the joint. The distal joint is a unidirectional bending joint [5], with an effective deformation length of 60 mm. The joint bends towards the side of the spring plate when compressed gas is injected into the joint.

3. Kinematic model of flexible finger

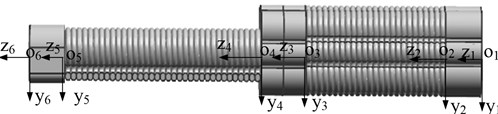
To facilitate the analysis on the position and posture of the finger, the coordinate system $O$-$X_j{Y}_j{Z}_j$ is established, where $j$ ($j=$1, 2, 3, 4, 5, 6) denotes the feature points on the finger as showed in Fig. 2.

According to the deformation law of each joint and the geometric structure of the connecting piece, the transformation matrix of the two adjacent key points on the finger can be obtained when the fingers are forward bending.

The transformation of coordinates from the end to the other end of the unidirectional bending joint when it is bending can be expressed as:

where ${\theta }_j$ is the bending angel of the joint. According to the deformation of the joint and its length, the following equations can be known:

where $D=$ 16 mm is the distance from the center of the latex tube to the spring plate, $L=$ 60 mm is the effective deformation length of the joint.

Fig. 1Three-dimensional model of the finger

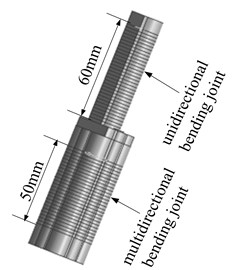
Fig. 2Coordinate system of the finger

Similarly, the transformation of coordinates from the end to the other end of the multi-directional bending joint can be expressed as:

where ${\gamma }_j$ is the bending angel of the joint. According to the deformation of the joint and its length, the following equations can be known:

where $l_0=$ 60 mm is the effective deformation length of the joint, $\mathrm{\Delta }l$ is the elongation of the joint.

The transformation of coordinates from the end to the other end of the connector can be expressed as:

According to the geometric shape of the connector: $e_i=e_j$.

The vector representation of each key point on the finger in the local coordinate system is ${}_{}{}^j{W}_j={\left[\begin{array}{llll}0& 0& 0& 1\end{array}\right]}^T$. The description of any key point on the finger in the root coordinate system can be obtained:

where ${}_j{}^{j-1}T$ represents the transformation matrix when the key points on the finger are transformed from the coordinate system $j$ to $j-1$. In the same way, the transformation matrix of the reverse bending and lateral pendulum of the finger can be obtained.

4. Experiment and simulation analysis

The changes of elongation and bending angle with air pressure were obtained by static experiments, which are shown in Figs. 3-5 respectively.

Fig. 3The curve of the elongation and pressure of multi-directional bending joint

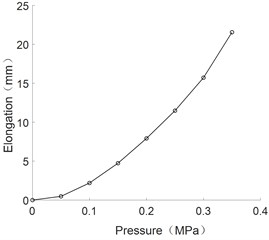
Fig. 4The curve of bending angle and pressure of unidirectional bending joint

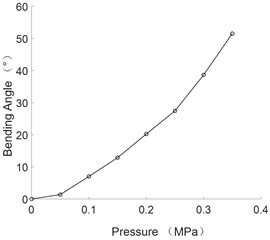
Fig. 5The curve of bending angle and pressure of multi-directional bending joint

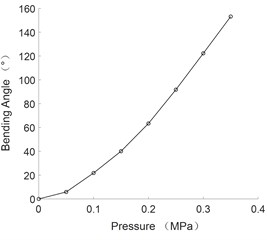
As can be seen from the figure, the bending angle of flexible joints and the axial elongation are positively correlated with the pressure value.

The experimental data were fitted by quadratic polynomial and the corresponding empirical formula was obtained as follows:

where $\mathrm{\Delta }l$ is the elongation of the of multi-directional bending joint, $p$ is the value of air pressure:

where $\mathrm{\Delta }\theta$ is the elongation of the of multi-directional bending joint:

where $\mathrm{\Delta }\gamma$ is the bending angle of the of unidirectional bending joint.

The pneumatic control principle of the finger is shown in Fig. 6, which is composed of six electric proportional valves and five electromagnetic directional valves. The electromagnetic directional valve is used to control the air pressure on and off and the proportional valve is used to regulate the gas pressure. Fig. 7 shows the different postures of the finger.

Fig. 6The pneumatic control principle

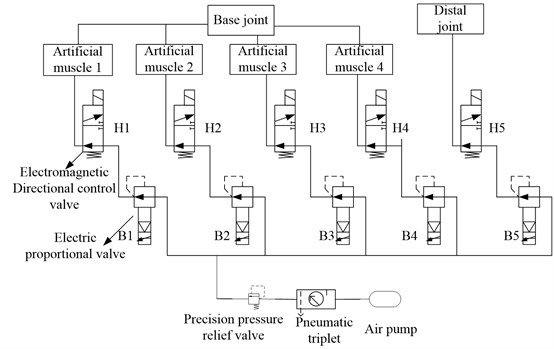
Fig. 7Different gestures of the finger

a) Forward bending

b) Reverse bending

c) Lateral swing

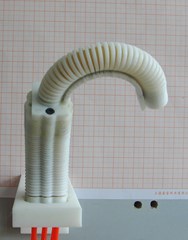
d) Lateral swing

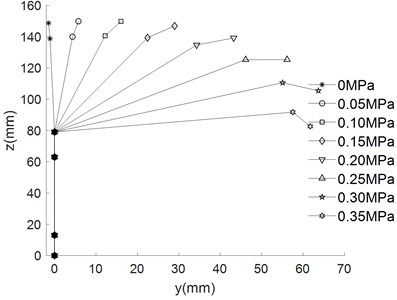
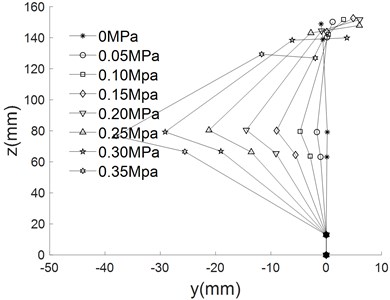
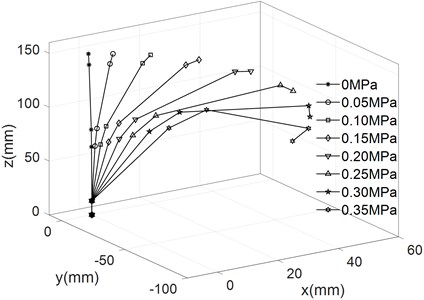
The empirical formula above are substituted into kinematic equation to obtain the different movement trajectory of the finger, which are shown in Fig. 8.

As can be seen from Fig. 8, the bending angle of the finger increases with the increase of air pressure under different driving modes. When the pressure is 0.35 MPa, the forward bending angle reached 208.8°, the reverse bending angle is 105.2°, the lateral swing bending angle is 51.51°. The base joint is multi-directional bending joint, which can be deformed in the $YZ$ plane (Fig. 5(a) to Fig. 5(d)). The base joint can also be deformed in the $XZ$ plane (Fig. 5(e) to realize the side swing function of the finger.

Fig. 8Different movement trajectory of finger

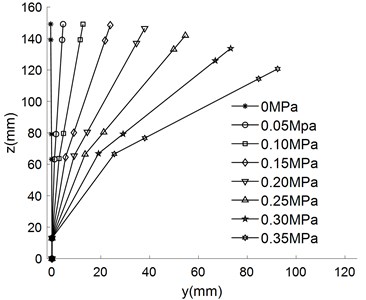
a) Base joint drives independently

b) Distal joint drives independently

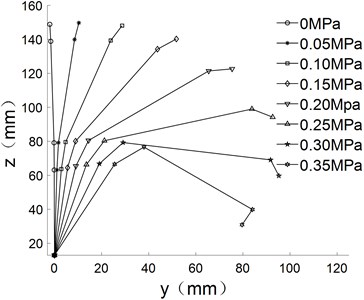
c) Forward bending

d) Reverse bending

e) Lateral swing

Through the comparison between the real experiment of fingers and the kinematic simulation results of flexible fingers, it can be seen that the simulation results of finger deformation are basically consistent with the experiment results, which shows that the established kinematic model of flexible fingers can well describe the deformation of fingers.

5. Conclusions

1) The biggest characteristic of the finger developed in this paper is that it is directly driven by artificial muscle, does not need decelerating device and transmission device and has certain elasticity and good cushioning.

2) The static experiment of the flexible joint is carried out and the change rule of the bending angle and the axial elongation of the joints with the air pressure is obtained. When the air pressure is 0.35 MPa, the maximum bending angle of the multi-directional bending joint is 51.51°, the maximum axial elongation is 21.56 mm; the maximum bending angle of the unidirectional bending joint is 153.2°.

3) The kinematic equation of the finger is established by using the homogeneous coordinate change matrix and the movement trajectory of the finger is obtained and verified by experiments. The maximum bending angles of forward bending, reverse bending and lateral swing were 208.8°, 105.2° and 51.51° respectively when the air pressure is 0.35 MPa. The experimental and simulation results show that the finger movements are flexible, which can realize forward bending, reverse bending and lateral swing. The complex gesture and grasping action can be realized by the cooperation of multiple flexible fingers.