Optimal design parameters of drum’s isolation system for a double-drum vibratory roller

Quynh, Le Van; Thao, Vi Thi Phuong; Phong, Truong Tu

doi:10.21595/vp.2020.21445

Vibroengineering Procedia

Browse Procedia

Published: 07 May 2020

Check for updates

Optimal design parameters of drum’s isolation system for a double-drum vibratory roller

Le Van Quynh¹

Vi Thi Phuong Thao²

Truong Tu Phong³

¹Faculty of Automotive and Power Machinery Engineering, Thai Nguyen University of Technology, Thai Nguyen, Vietnam

²Faculty of International Training, Thai Nguyen University of Technology, Thai Nguyen, Vietnam

³Center for Technical Practice, Thai Nguyen University of Technology, Thai Nguyen, Vietnam

Corresponding Author:

Le Van Quynh

Cite the article Download PDF

Downloads 1330

CrossRef Citations 7

Abstract

The aim of this study is to propose an optimal design method for drum’s isolation systems of a double-drum vibrating roller so that the ride comfort can be improved. A half-vehicle ride dynamic model is established based on the drum-ground interactions. The weighted root mean square (rms) of acceleration responses of the vertical and pitch vibrations of the vehicle body ( $a_{w b}$ and $a_{w p h i}$ ) according to the ISO 2631:1997(E) standard is chosen as objective functions. A genetic algorithm (GA) is applied for searching for the optimal design parameters of drum’s isolation systems based on the objective functions. The study results indicate that the $a_{w b}$ and $a_{w p h i}$ values of GA optimal parameters reduce significantly in comparison with those of the original parameters of drum’s isolation systems, which means that the performance optimization of drum’s isolation systems is better than the original vehicle in improving the vehicle ride comfort.

Optimal design parameters of drum’s isolation system for a double-drum vibratory roller

Highlights

The optimal design method for drum’s isolation systems of a double-drum vibrating roller is proposed in this study.
The genetic algorithm (GA) is applied for searching for the optimal design parameters of drum’s isolation systems.
The performance optimization of drum’s isolation systems is better than the original vehicle in improving the vehicle ride comfort.

1. Introduction

Vibratory roller operates and moves on various kinds of soil ground. The vibration excitation sources causing vehicle’s body vibration are not only the excitations of the interaction between drum and deformation ground soil, but also the excitations of vibration drum and engine which are one of the main reasons for the driver fatigue and their working efficiency. The ride comfort of the vehicle has gained increasing attention and it is important to research on the dynamics of drum-frame and frame-cab systems and properties of the isolation system between them. The design parameters of cab’s passive isolation system of a single drum vibratory roller were surveyed and evaluated its effect on ride comfort using a 3-D nonlinear dynamic model [1]. The influence of variations in the drum, cabin, seat, and rear-axle suspension properties on ride comfort was analyzed based on a 12-DOFs (degrees of freedom) pitch-plane ride dynamic model [2]. Even, the riding comfort was evaluated based on a nonlinear dynamics model of a single drum vibratory roller being operated under the different soil grounds [3]. To improve cab ride comfort of a vehicle, there were the optimal design and control solutions for cab’s isolation system such as optimal design parameters for cab’s auxiliary vibrations isolator [4] and cab’s main isolation system [6], the PID-Fuzzy control for cab’s isolation system [5]. The vibratory roller is usually not equipped with the suspension system to link the frame and vehicle axles, and it is important to reduce the transmission vibration from drums to frame. Drum’s isolation systems plays an important role in reducing the transmission vibrations to the frame. The effect of the design parameters of drum's metal rubber isolation system of the double-drum vibratory roller on ride comfort was analyzed based on a 7-DOFs ride dynamic model [7]. The complex stiffness of the rubber absorber was optimized based on a 2-DOFs dynamic model and the objective functions such as the maximums of compact power product and minimal frame displacement [8]. A kind of MR damper was proposed and applied in drum’s isolation systems to improve the comfort performance of the vibratory road roller [9].

This study presents an optimal design method for drum’s isolation systems of a double-drum vibrating roller to improve the ride comfort considering a 4-DOFs half -vehicle ride dynamic model of a vehicle operating under different conditions. The genetic algorithm is applied for the optimal parameters of drum’s isolation systems to minimize the values of the objective functions, thus the best comfort of the driver will be achieved. Finally, the optimal design parameters of drum’s isolation systems are evaluated and compared to the ones of the original vehicle when the vehicle is operated under different conditions.

2. Half-vehicle ride dynamic model

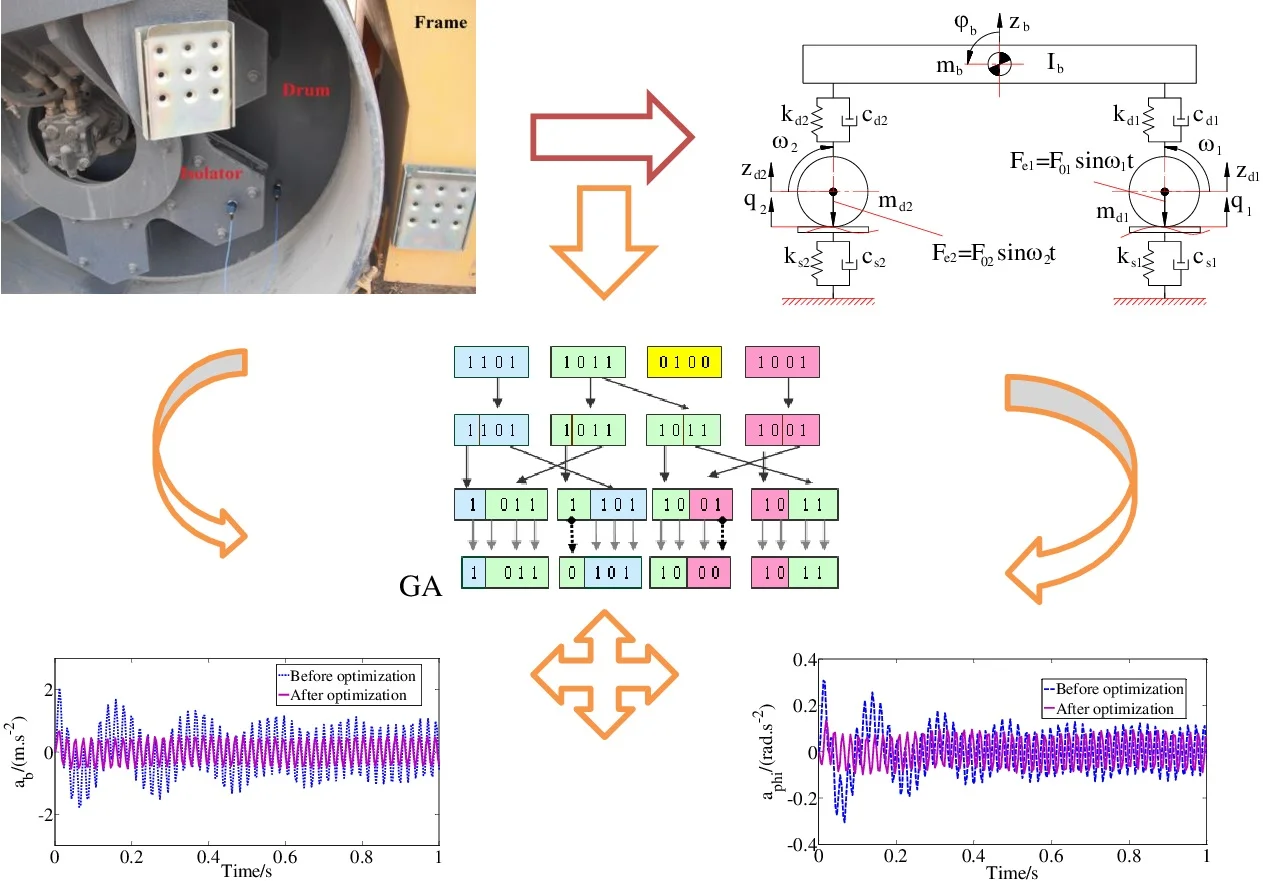
A rubber isolation system between the drum and frame is shown in Fig. 1(a). A half -vehicle ride dynamic model with four degrees of freedom shown in Fig. 1(b) is considered for searching for the optimal design parameters of drum’s isolation systems consisting of three main rigid bodies in which two drums and vehicle body are linked together by drum’s metal rubber isolation systems.

Fig. 1Double-drum vibrating roller

a) Side view of drum

b) Half -vehicle ride dynamic model

As shown in Fig. 1(b), $m_{d 1}$ , $m_{d 2}$ , and $m_{b}$ are the mass of the front drum, rear drum and vehicle body (including the frame, cab, and driver’s seat), respectively; $k_{d 1}$ , $k_{d 2}$ , and $c_{d 1}$ , $c_{d 2}$ are the stiffness and damping coefficients of the isolation system of the front and rear drums, respectively; $k_{s 1}$ , $k_{s 2}$ , and $c_{s 1}$ , $c_{s 2}$ are the stiffness and damping coefficients of the elastic soil ground contact with the front and rear drums, respectively; $z_{d 1}$ , $z_{d 2}$ , and $z_{b}$ are the vertical displacement of the front drum, rear drum and the vehicle body, respectively; $φ_{b}$ is the pitch angle displacements of the vehicle body; $I_{b}$ is the moment of inertia with respect to the y of the vehicle body; $q_{1}$ and $q_{2}$ are the excitation of ground surface contact with the front and rear drums, $F_{1} = F_{01} s i n ω_{1} t$ and $F_{2} = F_{02} s i n ω_{2} t$ .

The equations of motion for a double-drum vibrating roller using Newton’s second law of motion are written in two cases.

2.1. Case 1: vehicle moves into the workshop

Vehicle wheel contacts and moves on types of road or ground surfaces such as rigid, flexible, soft, etc. [10]. The drum of vibratory roller in contact with the rigid road surface is the contact point which is considered in this study.

From the half-vehicle ride dynamic model, as shown in Fig. 1(b), the motion equations of the front vehicle body mass are written as follows:

1

m_{b} {\ddot{z}}_{b} = - [k_{d 1} (z_{b} + l_{1} φ_{b} - q_{1}) + c_{d 1} ({\dot{z}}_{b} + l_{1} {\dot{φ}}_{b} - {\dot{q}}_{1})]

- [k_{d 2} (z_{b} - l_{2} φ_{b} - q_{2}) + c_{d 2} ({\dot{z}}_{b} - l_{2} {\dot{φ}}_{b} - {\dot{q}}_{2})],

2

I_{b} {\ddot{φ}}_{b} = [k_{d 2} (z_{b} - l_{2} φ_{b} - q_{2}) + c_{d 2} ({\dot{z}}_{b} - l_{2} {\dot{φ}}_{b} - {\dot{q}}_{2})] l_{2}

- [k_{d 1} (z_{b} + l_{1} φ_{b} - q_{1}) + c_{d 1} ({\dot{z}}_{b} + l_{1} {\dot{φ}}_{b} - {\dot{q}}_{1})] l_{1},

where, $q$ is the random road surface excitation according to the International Standards Organization (ISO) 8608 [14].

2.2. Case 2: vehicle operates in the workshop

When vehicle works and compresses on many different types of properties of deformable ground soil such as the hysteretic force – deflection properties [6], the elasto-plastic properties [2], [13]., etc. The properties of deformable ground soil are linear by the stiffness and damping coefficients of the elastic soil ground. From the half -vehicle ride dynamic model as shown in Fig. 1(b), the motion equations of the front drum mass, rear drum mass and vehicle body mass are written as follows:

3

m_{d 1} {\ddot{z}}_{d 1} = F_{01} s i n ω_{1} t + [k_{d 1} (z_{b} + l_{1} φ_{b} - q_{1}) + c_{d 1} ({\dot{z}}_{b} + l_{1} {\dot{φ}}_{b} - {\dot{q}}_{1})] - k_{s 1} z_{d 1} - c_{s 1} {\dot{z}}_{d 1},

4

m_{d 2} {\ddot{z}}_{d 2} = F_{02} s i n ω_{2} t + [k_{d 2} (z_{b} - l_{2} φ_{b} - q_{2}) + c_{d 2} ({\dot{z}}_{b} - l_{2} {\dot{φ}}_{b} - {\dot{q}}_{2})] - k_{s 2} z_{d 2} - c_{s 2} {\dot{z}}_{d 2},

5

m_{b} {\ddot{z}}_{b} = - [k_{d 1} (z_{b} + l_{1} φ_{b} - z_{d 1}) + c_{d 1} ({\dot{z}}_{b} + l_{1} {\dot{φ}}_{b} - {\dot{z}}_{d 1})]

- [k_{d 2} (z_{b} - l_{2} φ_{b} - z_{d 2}) + c_{d 2} ({\dot{z}}_{b} - l_{2} {\dot{φ}}_{b} - {\dot{z}}_{d 2})],

6

I_{b} {\ddot{φ}}_{b} = [k_{d 2} (z_{b} - l_{2} φ_{b} - z_{d 2}) + c_{d 2} ({\dot{z}}_{b} - l_{2} {\dot{φ}}_{b} - {\dot{z}}_{d 2})] l_{2}

- [k_{d 1} (z_{b} + l_{1} φ_{b} - z_{d 1}) + c_{d 1} ({\dot{z}}_{b} + l_{1} {\dot{φ}}_{b} - {\dot{z}}_{d 1})] l_{1},

3. Optimal isolation parameters via genetic algorithm

Assessing the off-road vehicle’s ride comfort: There are four methods to objectively evaluate ride comfort such as the international standard ISO 2631, the British standard BS 6841, VDI 2057, and while average absorbed power (AAP) [16]. The weighted root mean square (rms) of acceleration responses based on the international standard ISO 2631 is used as the objective function which is determined by the formula:

7

a_{w} = {[\frac{1}{T} \int_{0}^{T} a_{}^{2} (t) d t]}^{\frac{1}{2}},

where $a (t)$ is the weighted acceleration (translational and rotational) as a function of time in m/s²; $T$ is the duration of the measurements in s.

The genetic algorithm is a technique adapted from the evolutionary adaptation of biological populations by Darwinism. GA is a method of random optimization by mimicking the evolution of humans or organisms. Its idea is to simulate natural phenomena inheriting and fighting for survival. A simple genetic algorithm consists of the following steps: Step 1: Initialize a population of chromosome sequences; Step 2: Determine the target value for each corresponding chromosome; Step 3: Create new chromosomes based on genetic operators; Step 4: Eliminate low adaptive chromosomes; Step 5: Define the target function for new chromosomes and population inclusion. Step 6: Check whether the stop condition is satisfied. If the condition is right, get the best chromosome, and the algorithm stops; otherwise, go back to step 3.

Objective function: To improve the vehicle’s ride comfort, the optimal parameters of drum’s isolation systems are found out so that the values of the weighted root mean square (rms) of acceleration responses of cab’s vertical vibration ( $a_{w z}$ ) and pitch vibration ( $a_{w φ}$ ) should be minimized:

8

F (X) = w_{1} \{a_{w z} (X)\} + w_{2} \{a_{w φ} (X)\} \to m i n,

where, $w_{n}$ ( $n =$ 1, 2) are the weighting coefficients of sub-objective functions such that ( $w_{1} + w_{2} = 1$ ); $X = [k_{d 1}, k_{d 2}, c_{d 1}, c_{d 2}]$ is the design parameter vector of drum’s isolation systems.

Boundary conditions: The objective function Eq. (8) must satisfy the following boundary conditions:

9

\begin{matrix} \{\begin{array}{l} 0.9 \times 1 0^{6} \leq k_{d i} \leq 2.7 \times 1 0^{6}, \\ 2.5 \times 1 0^{3} \leq c_{d i} \leq 9 \times 1 0^{3}, \\ |z_{b i m a x} - z_{d i m a x}| \leq 1.2 \times 1 0^{- 3} . \end{array} i = 1, 2, \end{matrix}

4. Results and discussion

In order to find out the values of the optimal parameters of drum’s isolation systems of a double-drum vibrating roller, the differential equations of motion in case 1 and case 2 are solved through Matlab/Simulink environment with the initial vehicle design parameters as shown in Table 1. A program of genetic algorithm is written in Matlab to declare input parameters such as objective function Eq. (8) with $w_{1} =$ 0.75, $w_{2} =$ 0.25, boundary conditions Eq. (9), and GA parameters such as population size as 50 and generation as 200, which called by Simulink module function using the sim function. When vehicle compacts on the original place with the parameters of the elastic soil grounds in Table 1 at both front and rear drums with the excitation frequencies of drums as 48 Hz (This condition is chosen for the optimal parameters because vehicle is often operates in this condition and it has the greatest impact on the drivers’ health), the optimal values of the parameters of drum’s isolation systems are obtained by GA method in comparison with the original parameters, as shown in Table 2.

Table 1Parameters of a double-drum vibrating roller

Parameters	Values	Parameters	Values	Parameters	Values
$m_{d 1}$ / kg	2300	$k_{d 2}$ / (N/m)	1803×10³	$F_{01}$ / N	128×10³
$m_{d 2}$ / kg	2300	$c_{d 2}$ / (Ns/m)	3990	$F_{02}$ / N	96×10³
$m_{b}$ / kg	3270	$k_{s 1}$ / (N/m)	1×10⁷	$f_{1}$ / Hz	48/54
$I_{b}$ / kg m²	7811	$c_{s 1}$ / (Ns/m)	210×10³	$f_{2}$ / Hz	48/54
$k_{d 1}$ / (N/m)	1803x10³	$k_{s 2}$ / (N/m)	1.2×10⁷	$l_{1}$ / m	1.80
$c_{d 1}$ / (Ns/m)	3990	$c_{s 2}$ / (Ns/m)	280×10³	$l_{2}$ / m	1.80

Table 2GA optimization parameters of drum’s isolation systems

Parameters	$k_{d 1}$ / (N/m)	$c_{d 1}$ / (Ns/m)	$k_{d 2}$ / (N/m)	$c_{d 2}$ / (Ns/m)
Original values	1803×10³	3990	1803×10³	3990
Optimal values by GA	1017×10³	2804	255×10³	6130

The performances of the GA are compared with the original parameters of drum’s isolation systems when the vehicle operates at Case 2 with the excitation frequencies of drums as 48 Hz, as shown in Fig. 2.

From the results of Fig. 2, we can determine the values of the weighted rms acceleration of the vertical vehicle body ( $a_{w b}$ ) and pitch angle of vehicle body ( $a_{w p h i}$ ) according to Eq. (7) are 0.6963 m/s² and 0.0810 rad/s² with the original parameters of drum’s isolation systems and 0.3497 m/s² and 0.0604 rad/s² with GA optimal parameters of drum’s isolation systems. The results show that the $a_{w b}$ and $a_{w p h i}$ values with GA optimal parameters respectively reduce by 99.11 % and 34.11 % in comparison with the original parameters of drum’s isolation systems, which means that vehicle’s ride comfort is improved significantly when the vehicle operates in this condition.

The optimized results of GA are compared to those of the original parameters of drum’s isolation systems when the vehicle is operated at Case 2 with the different excitation frequencies of drums, as shown in Table 3. These results indicate that the $a_{w b}$ and $a_{w p h i}$ values of GA optimal parameters respectively reduce by 87.89 % and 22.67 % ( $f_{1} =$ 54 Hz and $f_{2} =$ 54 Hz), 42.03 % and 42.65 % ( $F_{10} =$ 0 and $f_{2} =$ 48 Hz), and 34.53 % and 34.92 % ( $F_{10} =$ 0 and $f_{2} =$ 54 Hz) in comparison with the original parameters of drum’s isolation systems, which means that the ride comfort of the double-drum vibrating roller is improved significantly.

Fig. 2The comparison of acceleration responses of vehicle body at Case 2

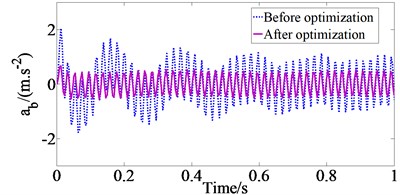
a) Vertical vehicle body

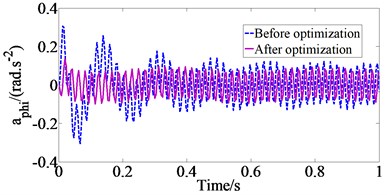
b) Pitch angle of vehicle body

Table 3Comparison of optimized results at Case 2 with the different excitation frequencies

Cases	$f_{1} =$ 54 Hz and $f_{2} =$ 54 Hz		$F_{10} =$ 0 and $f_{2} =$ 48 Hz		$F_{10} =$ 0 and $f_{2} =$ 54 Hz
Cases	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)
Original parameters	0.5723	0.0644	0.2984	0.2261	0.2466	0.1866
GA optimization	0.3046	0.0525	0.2101	0.1585	0.1833	0.1383
Decrease %	87.89	22.67	42.03	42.65	34.53	34.92

When the vehicle moves on the ISO class B road surface at the vehicle speed $v =$ 15 km/h (Case 1), the acceleration responses of the vertical vehicle body ( $a_{b}$ ) and the pitch angle of the vehicle body ( $a_{p h i}$ ) with GA optimal parameters in comparison with the original parameters of drum’s isolation systems are shown Fig. 3. From the results of Fig. 3, we can determine the $a_{w b}$ and $a_{w p h i}$ values are 0.9822 m/s² and 0.8142 rad/s² with the original parameters and 0.1960 m/s² and 0.1129 rad/s² with GA optimal parameters of drum’s isolation systems. The results show that $a_{w b}$ and $a_{w p h i}$ values with GA optimal parameters greatly reduce in comparison with the original parameters of drum’s isolation systems, which means that the performance optimization of drum’s isolation systems is better than the original isolation systems of drums in improving the ride comfort.

Fig. 3The comparison of acceleration responses of vehicle body at Case 1

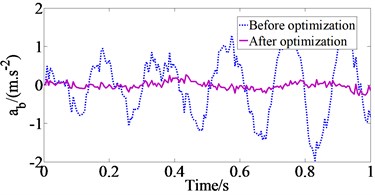
a) Vertical vehicle body

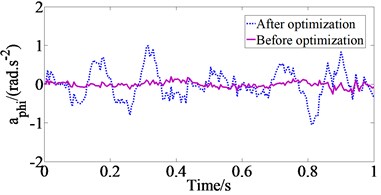
b) Pitch angle of vehicle body

Table 4Comparison of optimized results at Case 1 with the different road surface conditions

Cases	ISO class C		ISO class D		ISO class E
Cases	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)	$a_{w z}$ (m.s^-2)	$a_{w p h i}$ (rad.s^-2)
Original parameters	1.7673	1.4651	3.1023	2.5718	5.6108	4.6513
GA optimization	0.3528	0.2033	0.6194	0.3569	1.1203	0.6456
Decrease %	400.94	620.66	400.86	620.59	400.83	620.46

Similarly, the optimized results of GA are compared to those of the original parameters of drum’s isolation systems when the vehicle moves at the vehicle speed $v =$ 15 km/h (Case 1) with the different road surface conditions, as shown in Table 4. These results indicate that the performance optimization of drum’s isolation systems has been greatly improved the vehicle ride comfort. However, GA optimal parameters have not been considered for the ride performance on the frequency domain.

5. Conclusions

In this study, a half-vehicle ride dynamic model of a double-drum vibrating roller is established under different operating conditions for searching the optimal parameters for drum’s isolation systems to improve the ride comfort. A genetic algorithm is applied for searching the optimal parameters of drum’s isolation system order to minimize the $a_{w z}$ and pitch $a_{w φ}$ values in order to achieve the best comfort of a double-drum vibrating roller. The study results show that the $a_{w b}$ and $a_{w p h i}$ values with GA optimal parameters greatly reduce in comparison with the original parameters of drum’s isolation systems, which means that vehicle’s ride comfort is improved significantly. Also, the study results can provide the theoretical basis for the isolation system design of the vibrating rollers.

References

Le Van Quynh, Thao V. T. P., et al. Influence of design parameters of cab’s isolation system on vibratory roller ride comfort under the deformed ground surfaces. International Research Journal of Engineering and Technology (IRJET), Vol. 6, Issue 6, 2019, p. 1974-1978.

Search CrossRef
Kordestani Rakheja, et al. Analysis of ride vibration environment of soil compactors. SAE International Journal of Commercial Vehicles, Vol. 3, Issue 1, 2010, p. 259-272.

Publisher
Le V. Q., Zhang J. R., et al. Ride comfort evaluation of vibratory roller under different soil ground. Transactions of the Chinese Society of Agricultural Engineering, Vol. 29, 2013, p. 39-47.

Search CrossRef
Quynh L. V., Zhang J. R., et al. Vibration analysis and optimal design for cab’s isolation system of vibratory roller. Advanced Materials Research, Vol. 199, 200, p. 936-940.

Publisher
Vanliem Nguyen, Renqiang Jiao, et al. Performance of PID-Fuzzy control for cab isolation mounts of soil compactors. Mathematical Models in Engineering, Vol. 5, Issue 4, 2019, p. 137-145.

Publisher
Le V. Q., Nguyen K. T. Optimal design parameters of cab’s isolation system for vibratory roller using a multi-objective genetic algorithm. Applied Mechanics and Materials, Vol. 875, 2018, p. 105-112.

Publisher
Le Van Quynh, Thao V. T. P., et al. Study on influence of design parameters of drum’s metal rubber isolation system of double vibratory roller on ride comfort. International Research Journal of Engineering and Technology (IRJET), Vol. 6, Issue 6, 2019, p. 1647-1651.

Search CrossRef
Qin Sicheng, Chen Shuqing, et al. Analysis on the optimum mechanical property of an isolating System of Vibratory Roller. Transactions of the Chinese Society for Agricultural Machinery, Vol. 33, Issue 1, 2002, p. 77-79, (in Chinese).

Search CrossRef
Liu S. N., Yan S. R., et al. Dynamic and control of vibratory road roller based on Magneto-Rheological semi-active damper. Advanced Materials Research, Vol. 479, Issue 481, 2012, p. 1200-1204.

Publisher
Quynh Le Van Vibration Study and Control Cab of Vibratory Roller. Southeast University, Nanjing, China, 2013.

Search CrossRef
Sun Xiaojuan, Zhang Jianrun Performance of earth-moving machinery cab with hydraulic mounts in low frequency. Journal of Vibration and Control, Vol. 20, Issue 5, 2014, p. 724-735.

Publisher
Le V. Ride comfort analysis of vibratory roller via numerical simulation and experiment. DEStech Transactions on Engineering and Technology Research, 2017.

Publisher
Liem N. V., Run Z. J., et al. Vibration analysis and modeling of an off-road vibratory roller equipped with three different cab’s isolation mounts. Shock and Vibration, Vol. 2018, 2018, p. 8527574.

Publisher
ISO 8068. Mechanical Vibration-Road Surface Profiles-Reporting of Measured Data. International Organization for Standardization, 1995.

Search CrossRef
ISO 2631-1. Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-Body Vibration, Part I: General Requirements. The International Organization for Standardization, 1997.

Search CrossRef
Els P. S., Theron N. J., et al. The ride comfort vs. handling compromise for off-road vehicles. Journal of Terramechanics, Vol. 44, Issue 4, 2007, p. 303-317.

Publisher

Cited by

Advances in Engineering Research and Application

Bui Van Cuong | Canh Chi Huan | Le Van Quynh | Doan Thanh Binh

(2023)

Advances in Engineering Research and Application

Canh Chi Huan | Dang Viet Ha | Le Anh Vu | Tran Van Thoan | Le Van Quynh

(2023)

Research on the Rolling Process of SMA-13 Asphalt Surface Layer for Bridge Decks Based on Compaction and Skid Resistance Equilibrium Problems

Zhilin Zhou | Wenting Zhang | Guosong Liang | Bo Chen | Junjian Yan

(2023)

Advances in Engineering Research and Application

Le Van Quynh | Le Anh Vu | Bui Van Cuong | Hoang Anh Tan | Le Xuan Long

(2022)

Advances in Engineering Research and Application

Le Van Quynh | Nguyen Tien Duy | Nguyen Van Liem | Bui Van Cuong | Le Xuan Long

(2021)

Improvement of Ride Comfort Quality for an Earth-Moving machinery with Semi-Active Cab Isolation System

(2021)

Optimal design parameters of air suspension systems for semi-trailer truck. Part 2: results and discussion

Nguyen Van Tuan | Le Van Quynh | Vi Thi Phuong Thao | Le Quang Duy

(2020)

About this article

Received

27 April 2020

Accepted

04 May 2020

Published

07 May 2020

SUBJECTS

Vibration in transportation engineering

DOI

https://doi.org/10.21595/vp.2020.21445

Keywords

vibratory roller

drum

isolation system

design parameter

genetic algorithm

ride comfort

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 02 16

Research on ride comfort of vibratory rollers: Part-2 Cab’s semi-active HPM with fuzzy control

Yuehan Li, Vanliem Nguyen, Xiaoyan Guo, Yan Kang

Research article

2021 02 05

Research on ride comfort of vibratory rollers: Part-1 Study on the effect of different cab isolation mounts

Yan Kang, Vanliem Nguyen, Xiaoyan Guo, Yuehan Li

Research article

2020 06 30

Development of cab isolation systems of off-road vibratory rollers: review research

Vanliem Nguyen, Vanquynh Le

Research article

2020 05 07

Experimental modal analysis and optimal design of cab’s isolation system for a single drum vibratory roller

Le Van Quynh, Zhang Jianrun, Nguyen Van Liem, Bui Van Cuong, Le Xuan Long, Do Thanh Phuong

L. V. Quynh, V. T. P. Thao, and T. T. Phong, “Optimal design parameters of drum’s isolation system for a double-drum vibratory roller,” Vibroengineering PROCEDIA, Vol. 31, pp. 74–79, May 2020, https://doi.org/10.21595/vp.2020.21445

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21445
UR  - https://doi.org/10.21595/vp.2020.21445
TI  - Optimal design parameters of drum’s isolation system for a double-drum vibratory roller
T2  - Vibroengineering PROCEDIA
AU  - Quynh, Le Van
AU  - Thao, Vi Thi Phuong
AU  - Phong, Truong Tu
PY  - 2020
DA  - 2020/05/07
PB  - JVE International Ltd.
SP  - 74-79
VL  - 31
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Quynh_2020,
	doi = {10.21595/vp.2020.21445},
	url = {https://doi.org/10.21595/vp.2020.21445},
	year = 2020,
	month = {may},
	publisher = {{JVE} International Ltd.},
	volume = {31},
	pages = {74--79},
	author = {Le Van Quynh and Vi Thi Phuong Thao and Truong Tu Phong},
	title = {Optimal design parameters of drum's isolation system for a double-drum vibratory roller},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]L. V. Quynh, V. T. P. Thao, and T. T. Phong, “Optimal design parameters of drum’s isolation system for a double-drum vibratory roller,” Vibroengineering PROCEDIA, vol. 31, pp. 74–79, May 2020, doi: 10.21595/vp.2020.21445.

Copy IEEE

Copied to clipboard!

Quynh, Le Van, Vi Thi Phuong Thao, and Truong Tu Phong. “Optimal Design Parameters of Drum’s Isolation System for a Double-Drum Vibratory Roller.” Vibroengineering PROCEDIA 31 (May 7, 2020): 74–79. https://doi.org/10.21595/vp.2020.21445.

Copy Chicago

Copied to clipboard!

Optimal design parameters of drum’s isolation system for a double-drum vibratory roller

Abstract

Highlights

1. Introduction

2. Half-vehicle ride dynamic model

2.1. Case 1: vehicle moves into the workshop

2.2. Case 2: vehicle operates in the workshop

3. Optimal isolation parameters via genetic algorithm

4. Results and discussion

5. Conclusions

References

Cited by

About this article

Related Articles