Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case

Ragulskis, K.; Spruogis, B.; Bogdevičius, M.; Matuliauskas, A.; Mištinas, V.; Ragulskis, L.

doi:10.21595/jmeacs.2020.21532

Journal of Mechanical Engineering, Automation and Control Systems

Browse Journal

Submit article

Published: 30 June 2020

Check for updates

Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case

K. Ragulskis¹

B. Spruogis²

M. Bogdevičius³

A. Matuliauskas⁴

V. Mištinas⁵

L. Ragulskis⁶

¹Kaunas University of Technology, K. Donelaičio Str. 73, LT-44249, Kaunas, Lithuania

^{2, 3, 4, 5}Department of Mobile Machinery and Railway Transport, Faculty of Transport Engineering, Vilnius Gediminas Technical University, Plytinės Str. 27, LT-10105, Vilnius, Lithuania

⁶Department of Systems Analysis, Faculty of Informatics, Vytautas Magnus University, Vileikos Str. 8, LT-44404, Kauna, Lithuania

Corresponding Author:

K. Ragulskis

Cite the article Download PDF

Downloads 880

Abstract

Generators of mechanical vibrations with nonlinear stiffness of the elastic element in the conservative case are investigated. It is shown that the vibrator of this type generates several harmonic components and that the number of those multiple harmonics can be controlled. One period of motion is investigated. The presented analytical relationships and numerically obtained graphical relationships reveal the qualities of the system and enable to choose the desirable parameters of motions. The performed investigation of this system showed that eigenvibrations take place with linear spectrums when the system in separate intervals consists from two linear parts. This takes place in the case when the border of difference of coefficients of stiffness is located in the position of equilibrium of the system. In both intervals vibrations by separate partial frequencies take place and general motion depends on the eigenfrequency of the whole system. Of course the latter frequency depends on both partial frequencies. General motion of the whole system takes place according to the infinite linear spectrum of eigenfrequencies. All this enables to create enhanced vibrators by using those qualities and to use them in technologies.

1. Introduction

In a number of publications basis of the theory of nonlinear mechanical generators of vibrations were investigated as well as their multi valued steady state regimes. The distinctive feature of this research work is in the fact that they can generate several frequencies under excitation of a single harmonic as well as ensure stable operation in the resonance zones.

This paper is based on the investigations of essentially nonlinear systems and their dynamics presented in a book by Ragulskienė V. Vibro-Shock Systems (Theory and Applications). Vilnius: Mintis, 1974, (in Russian), where change of the jump type in the characteristic of impact velocity which takes place at the point of transition between soft and hard excitations of vibrations is seen. But the essential features are not revealed. This quality was also observed when exciting vibrations of vibromotors in a book by Ragulskis K., Bansevičius R., Barauskas R., Kulvietis G. Vibromotors for Precision Microrobots. New York: Hemisphere, 1987. Here also attention was not directed to this quality. Papers presented in the references were useful for investigations. Nonlinear vibrating systems and their resonances are analysed in [1]. Periodic and transient excitations and the dynamics of impacts are investigated in [2]. Periodic nonlinear systems as well as their stabilization are analysed in [3]. Mechanical systems when impacts take place are investigated in [4]. Mechanical systems, impacts and their periodic orbits are described in [5]. Nonlinear vibro-impact energy sink is analysed in [6]. Impact of particle with a wall is investigated in [7]. Determination of frequencies of a mechanical system is analysed in [8]. Mechanism with a pendulum is described and investigated in [9]. Vibrations of a model having piecewise linearity are analysed in [10]. Resonant zones of a dynamical system are investigated in [11]. Investigation of the Sommerfeld effect is performed in [12]. Analysis of isolated resonances of a dynamical system is presented in [13].

Several systems were investigated in which subsystems with different nonlinearities have a point of transition and when this point in the static positions of both subsystems coincides, for example [14]. In this paper the investigation is presented when the quality of this type takes place and the independence of eigenfrequencies from the amplitudes of motions is determined and motion takes place with infinite spectrum of frequencies.

In this paper the system consisting from two subsystems the static positions of equilibrium of which coincide is investigated. The motions are investigated analytically – graphically and they indicate the linearity of spectrums with infinite number of frequencies.

The investigated system is described by the equations of the following type:

1

\ddot{x} + (p^{2} + p_{0}^{2}) x = f s i n (ω t + φ), x = x_{0},

2

\ddot{x} + p^{2} x = f s i n (ω t + φ), x < x_{0},

3

p_{0}^{2} x_{0} = 0, x < x_{0},

where $p = \sqrt{C / m}$ , $p_{0} = \sqrt{C_{0} / m}$ , $f = F / m$ , $ω$ and $φ$ are the frequency and phase of excitation respectively, $p$ and $p + p_{0}$ are partial eigenfrequencies of the system.

2. Conservative system

Characteristics of the system are determined analytically – numerically when $f = 0 .$

2.1. Motion of the system in the first interval

Investigation of motion of the system in the interval:

4

t \in [0, T_{0}], x = x_{0},

is performed.

The following conditions of motion are assumed when:

5

\begin{array}{l} t = 0, x = x_{0} = 0, \dot{x} = {\dot{x}}^{-}, \\ t = T_{0}, x = x_{0} = 0, \dot{x} = - {\dot{x}}^{-} . \end{array}

From the Eq. (1) by taking into account Eqs. (4) and (5) it is obtained:

6

x = \frac{{\dot{x}}^{-}}{\sqrt{p^{2} + p_{0}^{2}}} s i n \sqrt{p^{2} + p_{0}^{2}} t,

7

\dot{x} = {\dot{x}}^{-} c o s \sqrt{p^{2} + p_{0}^{2}} t,

8

\ddot{x} = - {\dot{x}}^{-} \sqrt{p^{2} + p_{0}^{2}} s i n \sqrt{p^{2} + p_{0}^{2}} t,

9

\dot{x} \ddot{x} = - 0.5 {({\dot{x}}^{-})}^{2} \sqrt{p^{2} + p_{0}^{2}} s i n 2 \sqrt{p^{2} + p_{0}^{2}} t .

From the Eq. (7) by taking into account Eqs. (5) it is obtained:

10

T_{0} = \frac{π}{\sqrt{p^{2} + p_{0}^{2}}} .

2.2. Motion of the system in the second interval

Investigation of motion of the system in the interval:

11

t \in [T_{a}, \bar{T}] = [T_{a}, \frac{2 π}{\bar{ω}}], x \leq x_{0},

where $\bar{T}$ and $\bar{ω}$ are the eigenperiod and eigenfrequency of the system respectively, is performed.

At:

12

t = \bar{T}, x = x_{0} = 0, \dot{x} = {\dot{x}}^{-} .

From the Eq. (3) by taking into account Eq. (5) it is obtained:

13

x = - \frac{{\dot{x}}^{-}}{p} s i n p (t - T_{0}),

14

\dot{x} = - {\dot{x}}^{-} c o s p (t - T_{0}),

15

\ddot{x} = {\dot{x}}^{-} p s i n p (t - T_{0}),

16

\dot{x} \ddot{x} = - 0.5 {({\dot{x}}^{-})}^{2} p s i n 2 p (t - T_{0}) .

From the Eq. (13) by taking into account Eqs. (10) and (12) it is obtained:

17

\bar{T} = \frac{π}{\sqrt{p^{2} + p_{0}^{2}}} + \frac{π}{p} o r \bar{T} = \frac{π}{p} [1 + \frac{1}{\sqrt{1 + {(\frac{p_{0}}{p})}^{2}}}] .

By taking into account that $\bar{T} = 2 π / \bar{ω}$ and on the basis of Eq. (16) it is obtained:

18

\bar{ω} = 2 p \frac{\sqrt{1 + {(\frac{p_{0}}{p})}^{2}}}{\sqrt{1 + {(\frac{p_{0}}{p})}^{2}} + 1},

which is used for the determination of the eigenfrequency as a function of the parameters of the investigated system.

2.3. Characteristics of the system

Dynamical characteristics of the system $x$ , $\dot{x}$ , $\ddot{x}$ , $\dot{x} \ddot{x}$ are expanded into the Fourier series with respect to the eigenfrequency.

As an example the expansion of the characteristics of displacement is presented. According to the Eqs. (5) and (13):

19

x = \frac{{\dot{x}}^{-}}{p} \{\begin{array}{l} \frac{1}{\sqrt{1 + {(\frac{p_{0}}{p})}^{2}}} s i n \sqrt{1 + {(\frac{p_{0}}{p})}^{2}} t, 0 \leq t \leq {\bar{T}}_{0} = \frac{π}{p \sqrt{1 + (\frac{p_{0}}{p})}}, \\ - s i n p (t - T_{0}), T_{0} \leq t \leq \bar{T}, \end{array}

it is obtained:

20

x = \frac{{\dot{x}}^{-}}{p} \sum_{n = 0}^{\infty} (a_{n} s i n n \bar{ω} t + b_{n} s i n n \bar{ω} t),

where $a_{n}$ and $b_{n}$ depend only from $p$ and $p_{0} / p .$

In the same way other characteristics are also expanded into the Fourier series:

21

\dot{x} = {\dot{x}}^{-} \{\begin{array}{l} c o s p \sqrt{1 + {(\frac{p_{0}}{p})}^{2}} t, 0 \leq t \leq T_{0}, \\ - c o s p (t - T_{0}), T_{0} \leq t \leq \bar{T}, \end{array}

22

\ddot{x} = {\dot{x}}^{-} p \{\begin{array}{l} - \sqrt{1 + {(\frac{p_{0}}{p})}^{2}} s i n p \sqrt{1 + {(\frac{p_{0}}{p})}^{2}} t, 0 \leq t \leq T_{0}, \\ s i n p (t - T_{0}), T_{0} < t < \bar{T}, \end{array}

23

\dot{x} \ddot{x} = - 0.5 {({\dot{x}}^{-})}^{2} p \{\begin{array}{l} \sqrt{p^{2} + \frac{p_{0}}{p}} s i n 2 p \sqrt{p + {(\frac{p_{0}}{p})}^{2}} t, 0 \leq t \leq T_{0}, \\ s i n 2 p (t - T_{0}), T_{0} < t < \bar{T} . \end{array}

According to the Eqs. (19) and Eqs. (21-23) their investigation is performed by obtaining graphical relationships $\dot{x} = \dot{x} (x)$ , $\ddot{x} = \ddot{x} (\dot{x})$ , $\dot{x} \ddot{x} = \dot{x} \ddot{x} (x)$ ; $x$ , $\dot{x}$ , $\ddot{x}$ , $\dot{x} \ddot{x}$ as functions of time in the period $\bar{T}$ and also the coefficients of their expansion into the Fourier series, that is the graphical representations of eigenfrequencies.

3. Results of investigations of dynamics of the conservative system

Graphical results of investigation of dynamics of the system when $p^{2} = 1$ , $p_{0}^{2} = 1$ are presented in Fig. 1.

Graphical results of investigation of dynamics of the system when $p^{2} =$ 1, $p_{0}^{2} =$ 4 are presented in Fig. 2.

Graphical results of investigation of dynamics of the system when $p^{2} = 4$ , $p_{0}^{2} = 1$ are presented in Fig. 3.

Amplitude frequency characteristics when $p^{2} =$ 1, $p_{0}^{2} =$ 1 are presented in Fig. 4.

Amplitude frequency characteristics when $p^{2} =$ 1, $p_{0}^{2} =$ 4 are presented in Fig. 5.

Amplitude frequency characteristics when $p^{2} =$ 4, $p_{0}^{2} =$ 1 are presented in Fig. 6.

Fig. 1Dynamics of the conservative system when p2= 1, p02= 1

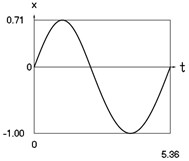
a) Displacement as function of time

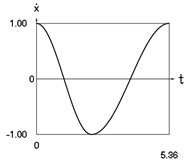
b) Velocity as function of time

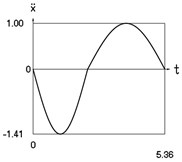
c) Acceleration as function of time

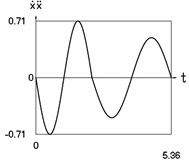
d) Velocity multiplied by acceleration as function of time

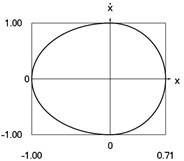
e) Phase trajectory: velocity as function of displacement

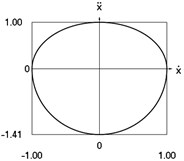
f) Phase trajectory: acceleration as function of velocity

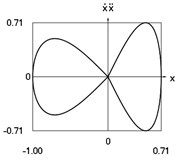
g) Phase trajectory: velocity multiplied by acceleration as function of displacement

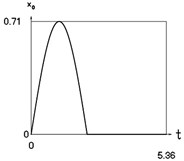
h) Another displacement as function of time

Fig. 2Dynamics of the conservative system when p2= 1, p02= 4

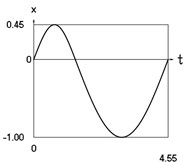
a) Displacement as function of time

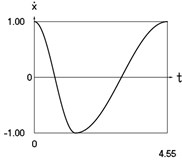
b) Velocity as function of time

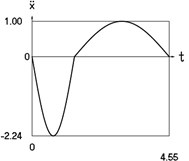
c) Acceleration as function of time

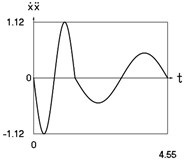
d) Velocity multiplied by acceleration as function of time

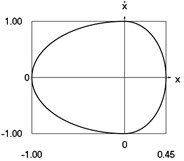
e) Phase trajectory: velocity as function of displacement

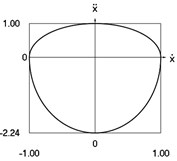
f) Phase trajectory: acceleration as function of velocity

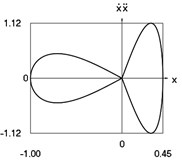
g) Phase trajectory: velocity multiplied by acceleration as function of displacement

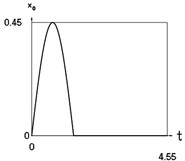
h) Another displacement as function of time

Fig. 3Dynamics of the conservative system when p2= 4, p02= 1

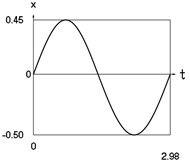
a) Displacement as function of time

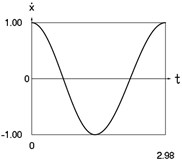
b) Velocity as function of time

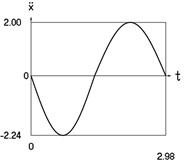
c) Acceleration as function of time

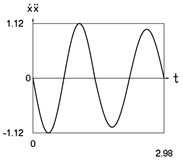
d) Velocity multiplied by acceleration as function of time

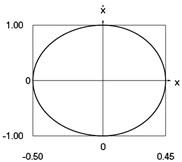
e) Phase trajectory: velocity as function of displacement

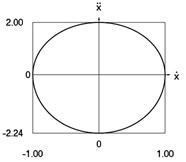
f) Phase trajectory: acceleration as function of velocity

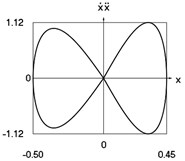
g) Phase trajectory: velocity multiplied by acceleration as function of displacement

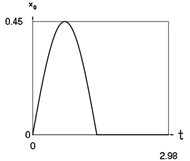
h) Another displacement as function of time

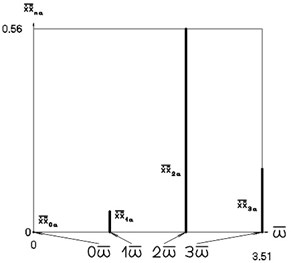
Fig. 4Amplitude frequency characteristics (constant part and first three harmonics) when p2= 1, p02= 1

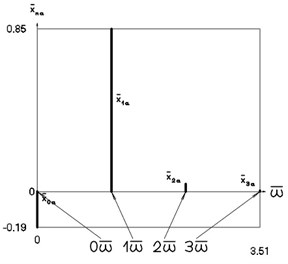
a) Displacement frequency characteristic

b) Velocity frequency characteristic

c) Acceleration frequency characteristic

d) Velocity multiplied by acceleration frequency characteristic

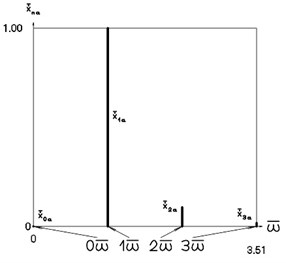
Fig. 5Amplitude frequency characteristics (constant part and first three harmonics) when p2= 1, p02= 4

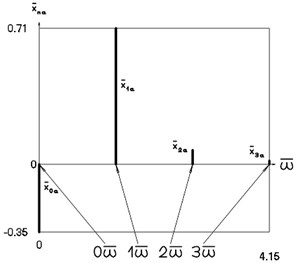
a) Displacement frequency characteristic

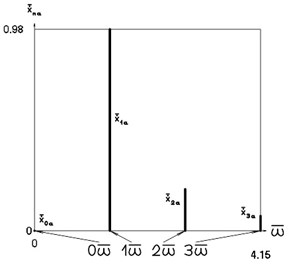
b) Velocity frequency characteristic

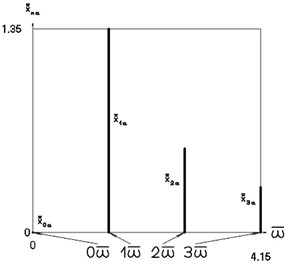
c) Acceleration frequency characteristic

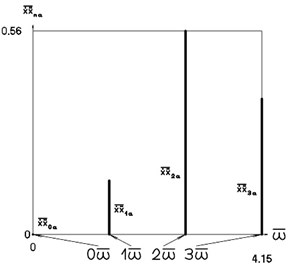
d) Velocity multiplied by acceleration frequency characteristic

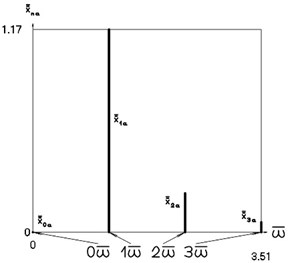
Fig. 6Amplitude frequency characteristics (constant part and first three harmonics) when p2= 4, p02= 1

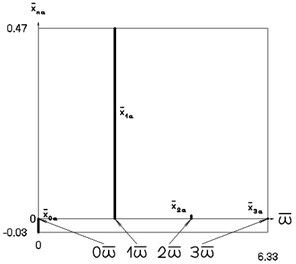
a) Displacement frequency characteristic

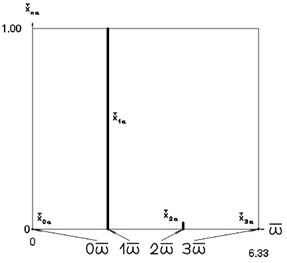
b) Velocity frequency characteristic

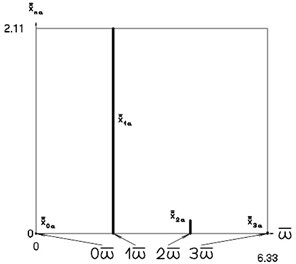
c) Acceleration frequency characteristic

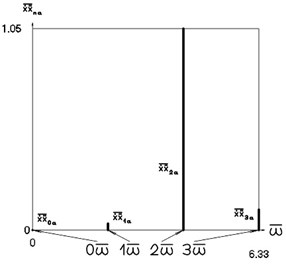
d) Velocity multiplied by acceleration frequency characteristic

4. Conclusions

General nonlinear model of the vibrator consists from two linear parts the coefficients of stiffness of the elastic element of which have different values and the positions of static equilibrium of the general system as well as positions of static equilibrium of both constituent parts are mutually equal. It is determined that the spectrum of eigenfrequencies of the general system is infinite and that values of frequencies do not depend from the amplitude of excitation. Vibrators of this type are effective, because in the resonance zones they do not have multivalued steady state regimes. The investigations were performed by using analytical – numerical methods and they revealed the qualities of the general system.

One period of motion of the conservative system is investigated. Results of investigation of dynamics of the conservative vibrating system for various parameters of the system are presented. Phase trajectories and amplitude frequency characteristics are used for representation of qualities of the system.

The presented analytical relationships and numerically obtained graphical relationships reveal the qualities of the system and enable to choose the desirable parameters of motions.

References

Wedig W. V. New resonances and velocity jumps in nonlinear road-vehicle dynamics. Procedia IUTAM, Vol. 19, 2016, p. 209-218.

Publisher
Li T., Gourc E., Seguy S., Berlioz A. Dynamics of two vibro-impact nonlinear energy sinks in parallel under periodic and transient excitations. International Journal of Non-Linear Mechanics, Vol. 90, 2017, p. 100-110.

Publisher
Zaitsev V. A. Global asymptotic stabilization of periodic nonlinear systems with stable free dynamics. Systems and Control Letters, Vol. 91, 2016, p. 7-13.

Publisher
Dankowicz H., Fotsch E. On the analysis of chatter in mechanical systems with impacts. Procedia IUTAM, Vol. 20, 2017, p. 18-25.

Publisher
Spedicato S., Notarstefano G. An optimal control approach to the design of periodic orbits for mechanical systems with impacts. Nonlinear Analysis: Hybrid Systems, Vol. 23, 2017, p. 111-121.

Publisher
Li W., Wierschem N. E., Li X., Yang T. On the energy transfer mechanism of the single-sided vibro-impact nonlinear energy sink. Journal of Sound and Vibration, Vol. 437, 2018, p. 166-179.

Publisher
Marshall J. S. Modeling and sensitivity analysis of particle impact with a wall with integrated damping mechanisms. Powder Technology, Vol. 339, 2018, p. 17-24.

Publisher
Salahshoor E., Ebrahimi S., Zhang Y. Frequency analysis of a typical planar flexible multibody system with joint clearances. Mechanism and Machine Theory, Vol. 126, 2018, p. 429-456.

Publisher
Starossek U. Forced response of low-frequency pendulum mechanism. Mechanism and Machine Theory, Vol. 99, 2016, p. 207-216.

Publisher
Wang S., Hua L., Yang C., Zhang Y., Tan X. Nonlinear vibrations of a piecewise-linear quarter-car truck model by incremental harmonic balance method. Nonlinear Dynamics, Vol. 92, 2018, p. 1719-1732.

Publisher
Alevras P., Theodossiades S., Rahnejat H. On the dynamics of a nonlinear energy harvester with multiple resonant zones. Nonlinear Dynamics, Vol. 92, 2018, p. 1271-1286.

Publisher
Sinha A., Bharti S. K., Samantaray A. K., Chakraborty G., Bhattacharyya R. Sommerfeld effect in an oscillator with a reciprocating mass. Nonlinear Dynamics, Vol. 93, 2018, p. 1719-1739.

Publisher
Habib G., Cirillo G. I., Kerschen G. Isolated resonances and nonlinear damping. Nonlinear Dynamics, Vol. 93, 2018, p. 979-994.

Publisher
Ragulskis K., Ragulskis L. Vibroimpact mechanism in one separate case. Mathematical Models in Engineering, Vol. 5, Issue 2, 2019, p. 56-63.

Publisher

About this article

Received

21 April 2020

Accepted

13 June 2020

Published

30 June 2020

DOI

https://doi.org/10.21595/jmeacs.2020.21532

Keywords

mechanical generators of vibrations

conservative system

harmonic excitation

nonlinear qualities

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 10 20

Generating rectilinear, elliptical, and circular oscillations of a single-mass vibratory system equipped with an enhanced twin crank-type exciter

Vitaliy Korendiy, Oleksandr Kachur, Rostyslav Predko, Oleh Kotsiumbas, Rostyslav Stotsko, Mykola Ostashuk

Research article

2023 06 25

Vibrator with two impacting pairs, one of them in the position of equilibrium

K. Ragulskis, L. Ragulskis

Research article

2019 09 30

Vibrations of the nonlinear system in which stationary harmonic excited multivalued regimes in the vicinities of resonances do not exist

K. Ragulskis, L. Ragulskis

Research article

2019 06 30

Vibroimpact mechanism in one separate case

K. Ragulskis, L. Ragulskis

K. Ragulskis, B. Spruogis, M. Bogdevičius, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case,” Journal of Mechanical Engineering, Automation and Control Systems, Vol. 1, No. 1, pp. 37–45, Jun. 2020, https://doi.org/10.21595/jmeacs.2020.21532

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jmeacs.2020.21532
UR  - https://doi.org/10.21595/jmeacs.2020.21532
TI  - Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case
T2  - Journal of Mechanical Engineering, Automation and Control Systems
AU  - Ragulskis, K.
AU  - Spruogis, B.
AU  - Bogdevičius, M.
AU  - Matuliauskas, A.
AU  - Mištinas, V.
AU  - Ragulskis, L.
PY  - 2020
DA  - 2020/06/30
PB  - JVE International Ltd.
SP  - 37-45
IS  - 1
VL  - 1
SN  - 2669-1361
ER  - 

Copy Ris

Copied to clipboard!

@article{Ragulskis_2020,
	doi = {10.21595/jmeacs.2020.21532},
	url = {https://doi.org/10.21595/jmeacs.2020.21532},
	year = 2020,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {1},
	number = {1},
	pages = {37--45},
	author = {K. Ragulskis and B. Spruogis and M. Bogdevi{\v{c}}ius and A. Matuliauskas and V. Mi{\v{s}}tinas and L. Ragulskis},
	title = {Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case},
	journal = {Journal of Mechanical Engineering, Automation and Control Systems}
}

Copy Bibtex

Copied to clipboard!

[1]K. Ragulskis, B. Spruogis, M. Bogdevičius, A. Matuliauskas, V. Mištinas, and L. Ragulskis, “Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case,” Journal of Mechanical Engineering, Automation and Control Systems, vol. 1, no. 1, pp. 37–45, Jun. 2020, doi: 10.21595/jmeacs.2020.21532.

Copy IEEE

Copied to clipboard!

Ragulskis, K., B. Spruogis, M. Bogdevičius, A. Matuliauskas, V. Mištinas, and L. Ragulskis. “Qualities of a Vibrator, the Elastic Element of Which Has Different Coefficients of Stiffness in the Two Intervals of Displacements, in a Separate Case.” Journal of Mechanical Engineering, Automation and Control Systems 1, no. 1 (June 30, 2020): 37–45. https://doi.org/10.21595/jmeacs.2020.21532.

Copy Chicago

Copied to clipboard!

Qualities of a vibrator, the elastic element of which has different coefficients of stiffness in the two intervals of displacements, in a separate case

Abstract

1. Introduction

2. Conservative system

2.1. Motion of the system in the first interval

2.2. Motion of the system in the second interval

2.3. Characteristics of the system

3. Results of investigations of dynamics of the conservative system

4. Conclusions

References

About this article

Related Articles