Abstract
Four-dimensional track prediction is the precise control of the time dimension of three-dimensional space at each stage of the flight. Accurate prediction of the aircraft trajectory is a prerequisite for the automation of air traffic control. This article reviews 4D track prediction technology, that is, particle motion-based prediction method, hybrid estimation-based prediction method and machine learning-based prediction method. At the end, combined with aircraft track data, the method of data mining is used to extract the flight profile and describe the applicable scope of each method. The contents of this paper can be used for reference in the research direction of 4D track prediction technology.
Highlights
- In this paper, four-dimensional track prediction methods are reviewed, different four-dimensional track prediction methods and their development process are introduced.
- The simulation is carried out with track data and the flight profile is extracted by DTW algorithm.
- Finally, the prospect of four-dimensional track prediction in the field of numerical calculation is prospected.
1. Introduction
In recent years, the rapid development of the air transport industry has provided convenience for people to travel. However, with the continuous growth of air traffic, problems such as flight delays and airspace congestion have occurred frequently. In 2009, global air passenger traffic reached 2,250,000 passengers. With the development of society and the improvement of people’s material life, by 2018, the global air passenger traffic reached 4,233,000 passengers, and the air passenger traffic increased by 88 %. The increase in air transportation demand has caused the airspace to become more and more crowded. This kind of growth will continue, and 3D based on flight plans alone will not solve the problem, so there is an urgent need to solve the problem of 4D aircraft trajectory prediction. 4D aircraft trajectory prediction refers to the prediction and calculation of the four-dimensional trajectory point sequence generated based on empirical data and initial planning information when the aircraft has not yet flown. On the one hand, accurate 4D trajectory prediction results help to detect and adjust conflicts between different flight trajectories in advance, reduce or even avoid the possibility of air flight conflicts, and improve air traffic safety. On the other hand, it helps to master the overall flight status of all sorties before the current time point, smooth traffic flow, and improve air traffic efficiency. Therefore, obtaining accurate 4D trajectory prediction results has become the focus of air traffic control technology research in major aviation countries.
This article reviews 4D trajectory prediction technology and introduces several methods with a wide range of current applications, namely particle-based prediction methods, hybrid estimation-based prediction methods and machine learning-based prediction methods. For aircraft track radar data, the DTW algorithm is used to extract the flight profile of the aircraft in order to better understand the flight process.
2. 4D track prediction method
With the continuous improvement of science and technology, scholars’ research on four-dimensional track prediction has also become more in-depth, so that the real-time and accuracy of prediction have been greatly improved, and the technology of track prediction is roughly divided into the following three: prediction based on particle motion, prediction based on mixed estimation, and prediction based on machine learning.
2.1. Prediction based on particle motion
The prediction based on particle motion is the most traditional prediction method. It mainly regards the aircraft as a particle, performs force analysis on it, and establishes the kinematics and dynamics model in combination with the aircraft performance model, so as to realize the prediction of four-dimensional trajectory. Its basic structure is the fusion of multiple modules such as track calculation, performance parameters and environmental status.
Among them, the trajectory calculation module is the core of the four-dimensional track prediction method based on particle motion. It uses the full energy equation to construct a trajectory calculation model [1] to realize the prediction of vertical profiles, that is, velocity profile and altitude profile. In 1995, Rhonda A. Slattery and Zhao [2] generated the trajectory of the aircraft from the initial position to the final position based on the trajectory synthesizer (TS). The “Runge Kutta” is used to solve the total energy equation, and the “trial method” is used to iteratively control the speed of designated arrival time. In 1996, Wang Dahai [3] proposed to use historical trajectories to generate height profiles and velocity profiles, and form 4D guidance commands to achieve 4D guidance to the end area. In 2005, Peng Ying [4] et al. proposed the principium of garden line and angle line conjecture, combined with dynamic data to propose a dynamic trajectory estimation method, and achieved good results in real-time track prediction. In 2008, Qu Yingjun [5] et al. proposed an improved model of dynamic trajectory estimation. On the basis of the original dynamic trajectory estimation model, firstly, the influence factor of wind was introduced to modify the dynamic model, and then through the uncertainty analysis of the actual track, the uncertainty disturbance factor is introduced on the basis of the original trajectory prediction model, which improves the accuracy of track prediction. In the same year, Porretta M. [6] et al. established a three-dimensional point quality model based on the BADA database to simulate aircraft flight, and wind factors were considered in the model. A new speed estimation algorithm based on aircraft performance and flight intention information is proposed, which is suitable for reliable track prediction. In 2009, Wang Chao [7] et al. proposed the concept of a basic flight model. Based on the characteristics of the flight phase, the basic flight model was used to construct the horizontal trajectory and vertical profile of the aircraft. Fit a complete 4D track according to the flight status information of the track feature points, realizing the prediction of track feature points and arrival time. In 2012, Soler [8] et al. used a hybrid optimal control algorithm to solve the multi-stage trajectory optimization problem. In 2014, Kaneshege J. [9] et al. proposed a method that can improve the reliability and robustness of the trajectory operation based on the kinematic model. The algorithm calculates the difference between no track prediction and track prediction based on fuel consumption, flight time and other indicators from two angles of horizontal trajectory and altitude profile, and the author simulates the flight prediction process through simulation experiments. In 2016, Zhang Junfeng [10] et al. introduced a discrete dynamic model on the basis of the original model to realize the four-dimensional track prediction of aircraft departure phase, effectively reducing the prediction position error and time error.
In the four-dimensional track prediction of an aircraft, it is necessary to combine the aircraft performance data to solve the model. Common performance parameter models include: GAME, ANP and BADA. GAME is constructed by EUROCONTROL and is suitable for the track prediction model of the full energy equation. ANP is mainly used in the field of aviation noise assessment, its strengths are the division of take-off climb and descent approach phases, and the ability to model aircraft thrust more accurately. BADA is the basic data of aircraft, which is the most widely used. It is a group of data composed of American Standard Code for Information Exchange.
Environmental factors mainly include wind, temperature, air pressure, and density. Because air temperature, air pressure, and density will be calculated by a general model with changes in altitude, the acquisition and processing of wind information is particularly critical. There are several ways to obtain wind information: (1) The meteorological information provided by the forecast center, such as the GRIB format data published by the European Medium-Term Weather Forecast Center, can be interpolated according to the predicted time and the location of the aircraft to obtain the relevant wind speed and wind direction information to realize the track prediction, Xing [11] et al. used the Cressman interpolation algorithm to spatially interpolate GRIB data to establish a route meteorological model, realized the modification of the meteorological model, and made the prediction results more accurate. (2) Aircraft Meteorological Data Relay (AMDAR), for example, Tang [12] et al. used AMDAR to realize the track prediction between cities. (3) Based on the regression algorithm [13], estimate the wind field data.
2.2. Prediction based on hybrid estimation
Hybrid estimation includes single-model estimation and multi-model estimation, which solves the problems of too many parameters and low prediction accuracy in the course of aerodynamics prediction.
Single model estimation includes Kalman Filter algorithm, Improved Kalman Filter algorithm and Adaptive Filter algorithm. In 1998, TongLiu [14] et al. applied the adaptive extended Kalman Filter algorithm to the wireless ATM network for the first time. In the local prediction, combined with its model, its positioning and instantaneous speed prediction reached a high accuracy. In 2014, Wang Taobo [15] et al. proposed an Improved Kalman Filter algorithm for real-time estimation of system noise in the prediction model, which improved the prediction accuracy. In 2015, Yang Xiaopeng [16] et al. improved the “current” statistical model. A new fuzzy membership function was presented to establish the “current” statistical model. Combined with the adaptive filtering algorithm, the simulation of track prediction is achieved, and the effect is better than CSAF.
Because the aircraft not only needs to consider the external motion during flight, but also its own state, that is, its horizontal and vertical three-dimensional state. So, in a complex aviation environment, single model estimation will be subject to many restrictions, a multi-model estimation is proposed – IMM algorithm [17] to solve this problem. But it is worth noting that the premise of multi-model estimation is to assume that the modal transition matrix is fixed, regardless of the real-time state, but it is actually related. Therefore, in 2006, Seah and Hwang [18] proposed an estimation algorithm for a stochastic linear hybrid system with continuous state correlation mode transition. Gaussian mixture approximation was used to overcome the complexity of the exponential growth of the estimation problem, and the trajectory tracking and state prediction of the target aircraft were realized. In 2007, Yepes and Hwang [19] also proposed a method to calculate the flight path by combining the aircraft motion state estimated by the hybrid estimation algorithm and the flight intention inferred from the flight control information, flight plan and flight environment, so as to provide more accurate information for the aircraft flight. At the same time, Hwang [20] applied it to the field of conflict detection and achieved good prediction results. In 2011, Zhang Junfeng [21] et al. improved the IMM algorithm. By combining the performance of the IMM algorithm, an improved interactive multi model (M-IMM) algorithm was proposed and achieved good results in the track prediction simulation. The information of wind in the same year is introduced into the state equation by Maeder U. [22] et al, which improves the accuracy of track prediction.
2.3. Prediction based on machine learning
The prediction based on hybrid estimation and particle motion is the main method of four-dimensional track prediction, but with the development of big data, scholars have also done in-depth research on machine learning, as an important supplement to the four-dimensional track prediction method. The prediction based on machine learning usually mines the hidden information from a large number of data through mathematical algorithm, extracts the superset information, and then merges the remaining information to find the internal relationship, that is, the method based on data mining.
In 2007, Wu Jin [23] and others proposed a prediction model based on data mining in order to solve the problem that the traditional aerodynamic model has a large error in predicting the four-dimensional flight track. The model mainly mines historical flight time data, finds out the factors that affect the flight time, predicts the full flight time of the next flight, and then analyzes the historical position data to obtain the position of the aircraft at the beginning of each sampling period, thereby achieving completeness 4D track prediction, but the initial flight profile has not been identified. This aspect needs to be improved. In 2012, Song Leiliang [24] used an analogy between real-time radar tracks and track sets to achieve track prediction, but this method was limited by the scale of the track sets. In 2013, Leege A. [25] et al. proposed the use of actual aircraft trajectories and meteorological data to describe and evaluate machine learning methods for track prediction. In this method, historical data is used to train a model for time of arrival prediction. In 2014, Tastamberkov [26] et al. regarded track prediction as a functional regression problem, and solved it using wavelet decomposition to achieve track prediction between city pairs. In 2015, Hong and Lee [27] obtained the flight path pattern based on the clustering method, and then established a multiple logistic regression model to realize flight arrival time prediction. In the same year, Chen Qiang [28] et al. used radial basis function network (RBF) to construct the functional relationship between the height, speed, flight distance and flight time of the approaching aircraft when entering the port. In 2016, Ma Yong [29] proposed a four-dimensional precise track prediction algorithm based on data mining. The algorithm selects the historical flight that best matches the current input conditions when building a prediction model for prediction by mining and analyzing a large amount of historical flight data. The trajectory is output as a four-dimensional track, and this method is also limited by the set size of historical flight trajectories. Based on the uncertainty propagation law, an adaptive prediction model for the uncertainty of flight time with Mach number, flight distance, wind and temperature is derived by Noboru Takeichi [30] in 2018. The coefficients of the adaptive prediction model are determined by cluster analysis and linear regression analysis.
3. Extraction of reference track
In recent years, the fusion of scientific computing and artificial intelligence is gradually emerging. In the field of track prediction, the performance is to extract the reference track based on the historical big data combined with the calculation method, and then modify the real-time track according to the reference track, so as to achieve the effect of real-time prediction. In 2011, Gariel [31] et al. used the K-means clustering method to analyze the track in terminal area through radar data analysis and processing, and applied it to airspace monitoring. However, due to the limitation of radar coverage, this method cannot get a complete flight profile. K-means clustering actually uses Euclidean distance to judge the similarity of two tracks, but Euclidean distance cannot effectively represent the similarity between two sequences to some extent. In 2013, Lu Yiyu [32] proposed a model based entirely on historical flight data, and fitted the flight altitude profile of the aircraft based on the dynamic time warping distance (DTW) of the clustered track. In 2015, Xing [11] et al. proposed DSW algorithm to extract nominal height profile on the basis of DTW, and improve the accuracy of track prediction. Obviously, DTW algorithm is better than the traditional Euclidean distance in the similarity of time series, and the effect is relatively good.
3.1. DTW algorithm principle
DTW algorithm is often used in the comparison of time series. Because the length of the two time series may not be equal, the traditional Euclidean distance cannot be used in the comparison. It has a wide range of applications in the field of speech recognition. The problems are that different people have different speech speeds, or different pronunciation of the same letter, so that the length of time is different. As long as the time sequence of the time points is guaranteed, the time dimension of the track can be locally stretched and scaled, that is, it is not necessary to compare the positions at each time point. Therefore, DTW algorithm can be applied to calculate the minimum distance between tracks as the similarity between tracks under the condition that the time sequence is constant. And then find a representative track, that is, the nominal track.
Suppose and , , respectively represent two trajectories, from which we get a dimensional grid structure, where the points on the grid correspond to the difference between the height points and of the trajectory, and .
Fig. 1Curved path diagram
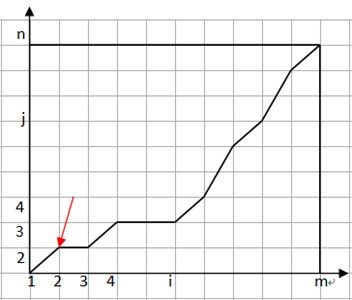
Where the curved path is , and the -th element of is the curved path as shown in the figure above, where the red line refers to , which represents the distance between the height points and , and this path satisfies the following conditions:
a)
b)
c) For .
Then there is:
Assuming that there are n aviation trajectories, respectively , if you want to find a representative one from them, you need to compare DTW with and other trajectories first, and record that the shortest distances of their curved paths as . Then compare the DTW distance of with other tracks, the shortest distance is . And so on, the DTW distance between all tracks and other tracks is obtained, and finally the final distance is calculated, that is, the track with the smallest sum of DTW distances from other tracks is taken as the nominal track.
3.2. Case simulation
This article will use radar data to observe the flight number CES5701, flights from ZPPP to ZBAA, and select 6 historical flight data to generate the initial trajectory.
Part of its data is shown in Fig. 2.
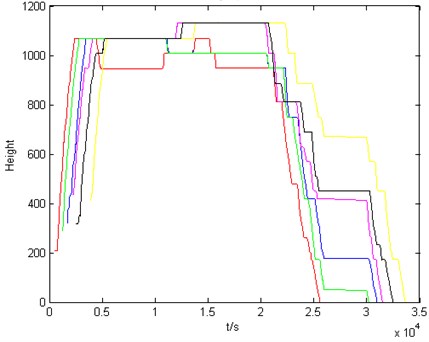
After fitting the above data, the height profile is obtained as shown in Fig. 3.
Fig. 2Radar data
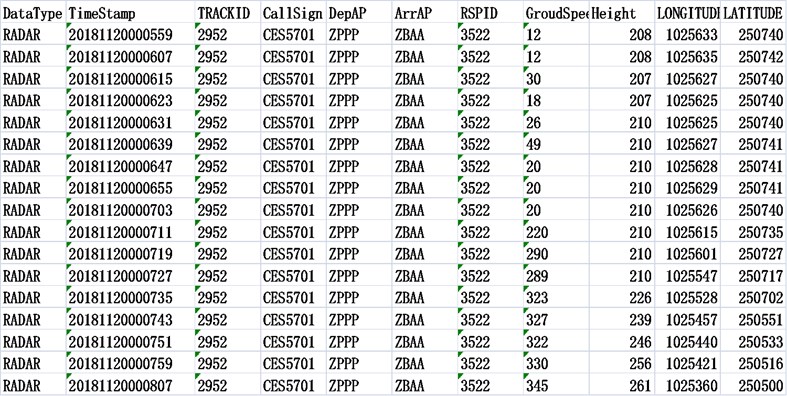
Fig. 3Height profile
Perform DTW calculation to get the DTW distance between these 6 tracks and other tracks. The results are shown in Table 1.
After that, find the sum of the distance between each track and other tracks, respectively: 190 km, 116 km, 121 km, 201 km, 113 km, 117 km.
From this, we can see that the sum of the distance between and other tracks is the smallest, then is the nominal height profile, as shown in Fig. 4.
Table 1DTW distance
Distance/km | L1 | L2 | L3 | L4 | L5 | L6 |
L1 | 0 | 20 | 45 | 65 | 19 | 41 |
L2 | 20 | 0 | 25 | 45 | 2 | 24 |
L3 | 45 | 25 | 0 | 22 | 25 | 4 |
L4 | 65 | 45 | 22 | 0 | 44 | 25 |
L5 | 19 | 2 | 25 | 44 | 0 | 23 |
L6 | 41 | 24 | 4 | 25 | 23 | 0 |
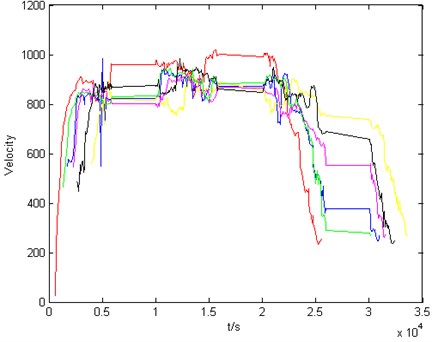
Its velocity profile is shown in Fig. 5. Perform DTW calculation on it to get the DTW distance between the 6 tracks and other tracks. The results are shown in Table 2.
Fig. 4Nominal height profile
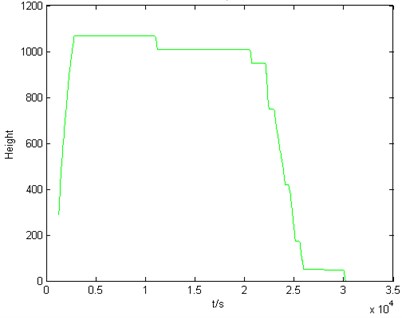
Fig. 5Velocity profile
After that, find the sum of the distance between each track and other tracks, respectively: 46 km, 29 km, 31 km, 28 km, 24 km, 26 km.
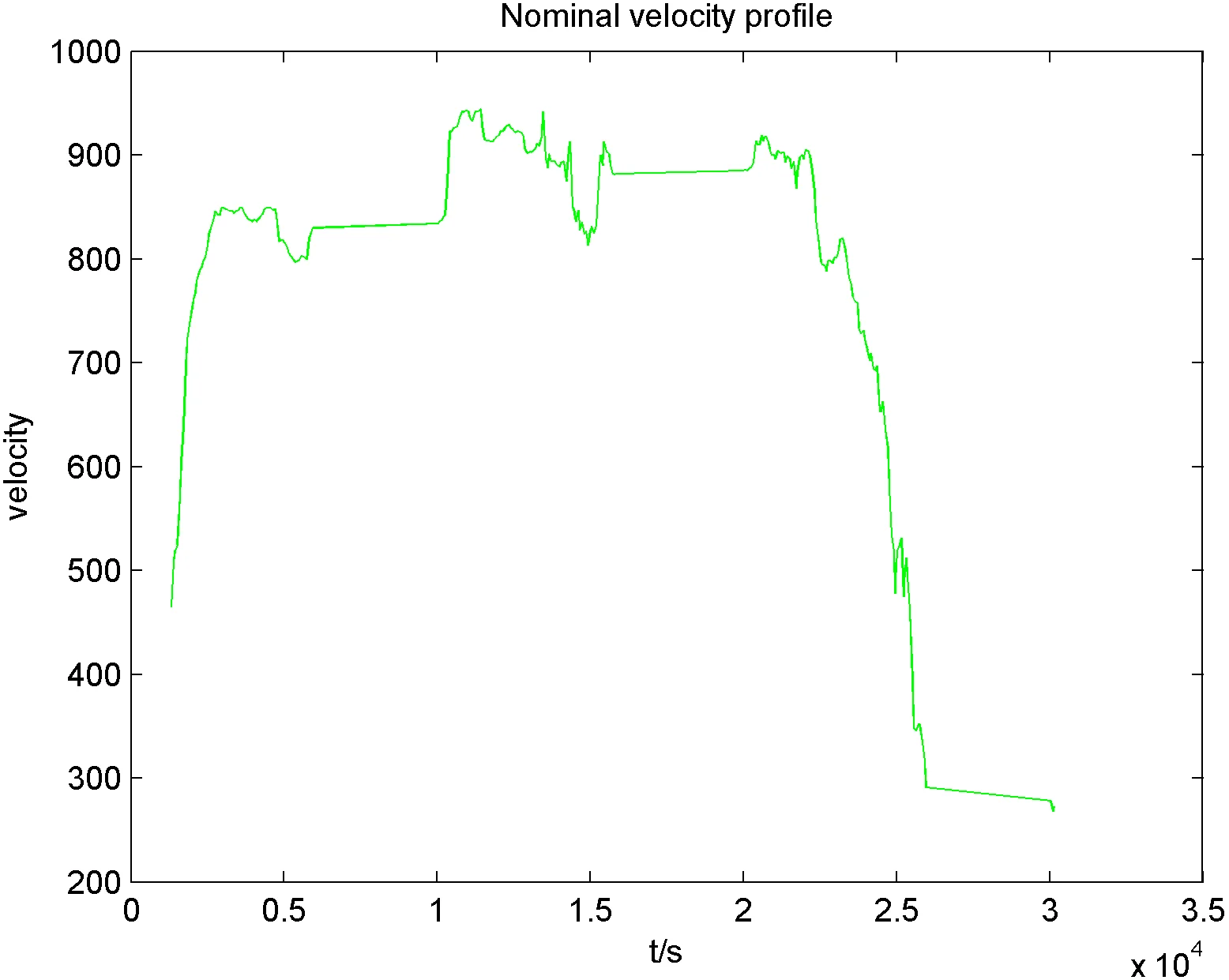
From this, we can see that the sum of the distance between and other tracks is the smallest, then is the nominal velocity profile, as shown in Fig. 6.
Fig. 6Nominal velocity profile
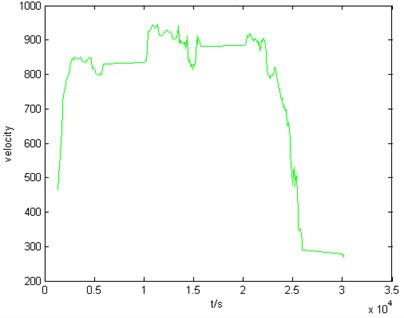
Table 2DTW distance
Distance/km | L1 | L2 | L3 | L4 | L5 | L6 |
L1 | 0 | 10 | 12 | 10 | 8 | 6 |
L2 | 10 | 0 | 5 | 5 | 4 | 5 |
L3 | 12 | 5 | 0 | 4 | 4 | 6 |
L4 | 10 | 5 | 4 | 0 | 4 | 5 |
L5 | 8 | 4 | 4 | 4 | 0 | 4 |
L6 | 6 | 5 | 6 | 5 | 4 | 0 |
4. Conclusions
This paper summarizes and describes the development of track prediction methods, and then introduces the main ideas of current track prediction under the background of the integration of scientific calculation and artificial intelligence. Through the simulation of flight radar data, the nominal flight profile of the aircraft is extracted by DTW algorithm. The application of track prediction determines the selection of track prediction methods. The track prediction method based on particle motion is the most classical and traditional method, and the system is more practical and applicable to a wide range, but it also has many parameters, so the method is applicable to track planning and other aspects. The essence of track prediction method based on hybrid estimation is to solve the problem of SLHS, so this method is suitable for conflict detection. The prediction method based on machine learning has great advantages in dealing with historical data in today’s big data era. It is applied to the mining of the internal relationship of historical flight data, and is more suitable for traffic management.
With the development of aviation industry, the air flow will continue to increase, and the theory and technology of four-dimensional track prediction need to be strengthened. In modern mathematical theory, Cressman interpolation method has been applied to the establishment of route weather model. On this basis, the Shepard interpolation model which can effectively solve the nonlinear problem can be considered for improvement. In the four-dimensional track fitting, the spline function can be considered to improve the continuity and smoothness of the curve. So that the air traffic control technology can complete the perfect transformation from the command based operation to the track based operation.
References
-
Accardo D., Moccia A., Fiorillo L., Leardi A., Maresca G. A trajectory prediction tool to support air traffic management. AIAA Infotech@Aerospace Conference, 2009.
-
Slattery R. A., Yiyuan Zhao En-route descent trajectory synthesis for air traffic control automation. Proceedings of the American Control Conference Washington, 1995, p. 3430-3434.
-
Wang Dahai Ground track counting method of the 4D guidance in terminal area. Flight Dynamics, Vol. 3, 1996, p. 27-33, (in Chinese).
-
Peng Ying, Hu Ming Hua, Zhang Ying Conjecture method of dynamic flying track. Journal of Traffic and Transportation Engineering, Vol. 1, 2005, p. 61-65, (in Chinese).
-
Qu Yingjun, Hu Minghua The improved model of aircraft dynamic trajectory prediction. Proceedings of the 4th China Intelligent Transportation Annual Conference 2008, (in Chinese).
-
Porretta M., Dupuy M. D., Schuster W., et al. Performance evaluation of a novel 4D trajectory prediction model for civil aircraft. Journal of Navigation, Vol. 61, Issue 3, 2008, p. 393-420.
-
Wang Chao, Guo Jiuxia, Shen Zhipeng Prediction of 4D trajectory based on basic flight models. Journal of Southwest Jiaotong University, Vol. 44, Issue 2, 2009, p. 295-300.
-
Soler M., Olivares A., Staffetti E., et al. Framework for aircraft trajectory planning toward an efficient air traffic management. Journal of Aircraft, Vol. 49, Issue 1, 2012, p. 341-348.
-
Kaneshige J., Benavides J., Sharma S., et al. Implementation of a trajectory prediction function for trajectory based operations. Proceedings of the AIAA Atmospheric Flight Mechanics Conference, 2014.
-
Zhang Junfeng, Ge Tengteng, Chen Qiang, Wang Fei 4D trajectory prediction and uncertainty analysis for departure aircraft. Journal of Southwest Jiaotong University, Vol. 51, Issue 4, 2016, p. 800-806, (in Chinese).
-
Xing Jian Air Traffic Guidance Technology Based on 4D Trajectory prediction with High Precision Method. Nanjing University of Aeronautics and Astronautics, 2015, (in Chinese).
-
Tang X. M., Chen P., Zhang Y. 4D trajectory estimation based on nominal flight profile extraction and airway meteorological forecast revision. Aerospace Science and Technology, Vol. 45, 2015, p. 387-397.
-
Kampoom J. W., Okolo W., Erturk S. A., et al. Wind field estimation and its utilization in trajectory prediction. AIAA Atmospheric Flight Mechanics Conference, 2015.
-
Tong L., Paramvir B. Mobility modeling, location tracking, and trajectory prediction in wireless ATM networks. IEEE Selected Areasin Communication, Vol. 16, Issue 6, 1998, p. 922-936.
-
Wang Taobo, Huang Baojun 4D flight trajectory prediction model based on improved Kalman filter. Journal of Computer Applications, Vol. 34, Issue 6, 2014, p. 1812-1815, (in Chinese).
-
Yang Xiaopeng, Ou Yangchao, Yang Zhaoyang, Yao Kun, Ni Juan A fuzzy adaptive algorithm based on current statistical model for track prediction. Journal of Air Force Engineering University (Natural Science Edition), Vol. 16, Issue 2, 2015, p. 1-4, (in Chinese).
-
Li X. R., Jilkov V. P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Transactions on Aerospace and Electronic Systems, Vol. 41, Issue 4, 2005, p. 1255-1321.
-
Hwang I., Seah C. E. An estimation algorithm for stochastic linear hybrid systems with continuous-state-dependent mode transitions. Conference on Decision and Control, 2006, p. 131-136.
-
Yepes J. L., Hwang I., Rotea M. A., et al. New algorithms for aircraft intent inference and trajectory prediction. Journal of Guidance Control and Dynamics, Vol. 30, Issue 2, 2007, p. 370-382.
-
Liu W., Hwang I. Probabilistic trajectory prediction and conflict detection for air traffic control. Journal of Guidance Control and Dynamics, Vol. 34, Issue 6, 2011, p. 1779-1789.
-
Zhang Junfeng, Wu Xiaoguang, Wang Fei Aircraft trajectory prediction based on modified interacting multiple model algorithm. Journal of Donghua University (English Edition), Vol. 32, Issue 2, 2015, p. 180-184.
-
Maeder U., Morari M., Baumgartner T., et al. Trajectory prediction for light aircraft. Journal of Guidance Control and Dynamics, Vol. 34, Issue 4, 2011, p. 1112-1119.
-
Wu Kun, Pan Wei 4D trajectory prediction model based on data mining. Computer Applications, Vol. 11, 2007, p. 2637-2639, (in Chinese).
-
Song Leiliang A 4D trajectory prediction method based on set of historical trajectory. Computer Technology and Development, Vol. 22, Issue 12, 2012, p. 11-14+20, (in Chinese).
-
Leege A., Paassen M., Mulder M. A machine learning approach to trajectory prediction. AIAA Guidance, Navigation, and Control (GNC) Conference, 2013.
-
Tastambekov K., Puechmorel S., Rabut C. Aircraft trajectory forecasting using local functional regression in sobolev space. Transportation Research Part C: Emerging Technologies, Vol. 39, 2014, p. 1-22.
-
Hong S., Lee K. Trajectory prediction for vectored area navigation arrivals. Journal of Aerospace Information Systems, Vol. 12, Issue 7, 2015, p. 490-502.
-
Chen Qiang, Zhang Jun Feng, Wang Fei, Zheng Zhixiang Arrival flight time prediction based on OLS-RBF neural networks. Aeronautical Computing Technique, Vol. 45, Issue 4, 2015, p. 42-45, (in Chinese).
-
Ma Yong Research on Precise Prediction Method of 4D Trajectory Based on Data Mining. Nanjing University of Aeronautics and Astronautics, 2016, (in Chinese).
-
Noboru Takeichi Adaptive prediction of flight time uncertainty for ground-based 4D trajectory management. Transportation Research Part C, Vol. 95, 2018, p. 335-345.
-
Gariel M., Srivastava A. N., Feron E. Trajectory clustering and an application to airspace monitoring. IEEE Transactions on Intelligent ransportation Systems, Vol. 12, Issue 4, 2011, p. 1511-1524.
-
Lu Yiyu Research on the Initial Flight Plan 4D Trajectory Generating and Simulation System. Nanjing University of Aeronautics and Astronautics, 2014, (in Chinese).
Cited by
About this article
The supports from the National Natural Science Foundation of China (Nos. 51674121 and 61702184), the Tangshan Team Project (No. 18130209B) and the Aviation Fund Project (No. 2017ZD41006) are gratefully acknowledged.
