Center trajectory extraction algorithm based on multidimensional hierarchical clustering

1. Introduction

With the increasing scale of China’s civil aviation industry and the gradual application of the digital management system, the operation data related to air traffic management is also increasing [1]. The flight path information of aircraft contains rich application value. The flight trajectory data scanned by radar are sorted according to the time stamp, and the position feature, time feature, and attribute feature are recorded. Therefore, how to make full use of multidimensional feature information from historical trajectory data, output meaningful traffic flow distribution [2, 3], and obtain center trajectory has become one of the research hotspots in the field of air traffic.

The central trajectory is the most representative one with the highest density in the traffic flow. The central trajectory can be applied to aircraft trajectory prediction [4], abnormal trajectory recognition [5], practical analysis of departure procedures [6], and airport noise control [7]. The main technical idea of central trajectory extraction is to measure the similarity between tracks and cluster large-scale track data into traffic flows with large intra-class similarity and small inter-class similarity [8-10]. Furthermore, the overall movement characteristics of traffic flow are found, so that a representative trajectory can be used to represent the group movement pattern of traffic flow [11]. In the aspect of center trajectory extraction, J. W. Han et al. Proposed the classic trajectory generation algorithm TRACLUS based on the idea of trajectory segmentation [12]; L. Zheng et al. Used the improved LR-1 algorithm to calculate the average value of trajectory points with the same serial number to get the center trajectory [13]. Wang Lili uses the LOFC time window segmentation algorithm to take the value of the minimum curvature in each trajectory to fit the center trajectory [14]. The center trajectories obtained by the above methods are all new synthetic trajectories, and there may not be any trajectories with the same path in the traffic flow, which does not conform to the actual operation of terminal area navigation. In addition, the synthesis method is time-consuming, and its computational complexity increases exponentially with the increase of the number of trajectories and sampling points. To solve the above problems, S. Du uses K-means clustering [15], F. Cheng uses density peak clustering [16], and S. R. Li uses spectral clustering [17] to find the trajectory with the highest density as the central trajectory. The above method uses the original trajectory as the center trajectory, but the output trajectory only contains position information. Without considering the influence of multidimensional attributes such as time, speed, heading and climb gradient, it cannot meet the requirements of trajectory prediction and abnormal trajectory recognition.

In this paper, the aircraft trajectory data in the radar terminal area is taken as the research object, and the problem of multidimensional feature center trajectory extraction is studied by using the data mining analysis method. Firstly, aiming at the problem that the existing trajectory clustering methods do not make full use of multidimensional features, on the one hand, the equal arc length interpolation resampling method is used to retain the real trajectory information; On the other hand, effective features are selected to calculate the similarity matrix with greater discrimination. Then the traffic flow distribution in the terminal area is obtained by multidimensional hierarchical clustering, and the center trajectory extraction model is established. Finally, the rationality and effectiveness of the proposed algorithm are verified by comparing with the traditional hierarchical clustering.

2. Data preprocessing

2.2. Resampling of multidimensional features by interpolation of equal arc length

Resampling is one of the core technologies in big data processing, which can effectively reduce the size of data while retaining the characteristics of data. Compared with linear interpolation [19], cubic spline interpolation [18] can better describe the trajectory movement characteristics, so this paper uses equal arc length interpolation resampling based on cubic spline interpolation to resample the trajectory. After defining the cubic spline interpolation function to calculate the original trajectory, the trajectory points are resampled according to the principle of equal arc length. Among them, the time and velocity are resampled in equal proportion according to the change of the value points of equal arc length, the heading is the tangential angle of the horizontal plane of the curve, and the climb gradient is the tangential angle of the vertical direction of the curve.

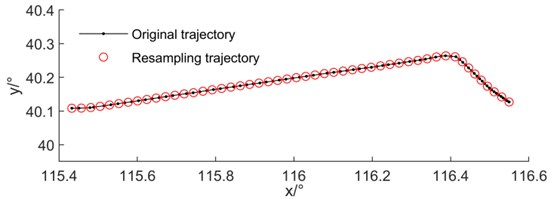
Resampling is shown in Fig. 1. The original position coordinates of the trajectory and the position coordinates after resampling are drawn on the same figure. The original object contains 96 trajectory points. In this paper, according to the idea of literature [20], after many experiments, the final determination of the number of sampling points is 50. Using the method of equal arc length interpolation resampling, the multidimensional characteristics of the trajectory can be accurately described when the sampling amount is 50. At the same time, this method greatly reduces the data scale and improves the running speed of the subsequent center trajectory extraction algorithm.

Fig. 1Schematic diagram of trajectory resampling

3. Center trajectory extraction algorithm

3.1. Similarity calculation based on multidimensional distance

The similarity calculation model of trajectories is the key factor affecting the rationality of clustering results. The traditional trajectory similarity calculation only focuses on the position feature, while the operation feature of space-time trajectory is multidimensional, so only calculating the position will cause large errors in calculation. Therefore, to reduce the error, this paper introduces the heading, climbing gradient and velocity of the real object trajectory. To improve the accuracy of trajectory similarity calculation and increase the differentiation of traffic flow in complex motion scenes. The trajectories $P_A=\left\{p_{A1},p_{A2},\cdot \cdot \cdot ,p_{Ai},\cdot \cdot \cdot ,p_{An}\right\}$ and $P_B=\left\{p_{B1},p_{B2},\cdot \cdot \cdot ,p_{Bi},\cdot \cdot \cdot ,p_{Bn}\right\}$ after resampling with equal arc length interpolation are defined, in which the sampling points of trajectories are equal.

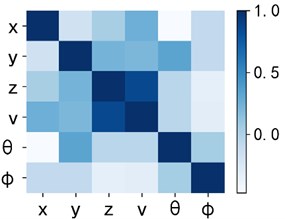
It is necessary to make a correlation analysis of the multidimensional characteristics of flight trajectory to determine their mutual influence relationship. In this paper, the correlation degree of each feature is found by Pearson coefficient correlation analysis. Fig. 2 is a thermal diagram of correlation, and the deeper the blue is, the stronger the correlation is. It can be seen from the figure that the correlation between speed and height is higher, and the correlation between other features is weak. Because the aircraft in the terminal area is in the acceleration stage and the altitude is rising, there is a certain correlation between altitude and speed. Therefore, it is determined that the distance between trajectories is still calculated by using six-dimensional data and the weight of speed is reduced appropriately.

Generally, the similarity between trajectories can be obtained by Euclidean distance [21], LCSS distance [22] and DTW distance [23]. The aircraft in the terminal area has high flight density, and the trajectory recorded by radar has the characteristics of different points, noise and strong maneuverability. Resampling not only unifies the number of tracks, but also reduces the influence of noise, so the Euclidean distance can be used to conveniently calculate the distance between tracks. Based on the six-dimensional characteristics of longitude, latitude, height, speed, direction and climb gradient, this paper uses the feature weighting method to calculate multidimensional distance, named weighted Euclidean distance (WED). The specific calculation formula is as follows:

1

$WED(P_A,P_B)=\sum _{i=1}^n\left[{\omega }_{1}dist\right(p_{Ai},p_{Bi})+{\omega }_{2}dist(v_{Ai},v_{Bi})+{\omega }_{3}dist({\theta }_{Ai},{\theta }_{Bi})+{\omega }_{4}dist({\phi }_{Ai},{\phi }_{Bi})].$

In Eq. (1), $dist(v_{Ai},v_{Bi})$ is the velocity Euclidean distance between trajectory points, $dist({\theta }_{Ai},{\theta }_{Bi})$ is the direction Euclidean distance between trajectory points, and $dist({\phi }_{Ai},{\phi }_{Bi})$ is the climbing gradient Euclidean distance between trajectory points; The weight should meet the following conditions: weight factor ${\omega }_i>0$, $i=\mathrm{1,2},\mathrm{3,4}$ and ${\omega }_1+{\omega }_2+{\omega }_3+{\omega }_4=1$. The weight factor can be adjusted according to the actual application scenarios, ${\omega }_1=$ 0.7, ${\omega }_2=$ 0.05, ${\omega }_3=$ 0.15, ${\omega }_4=$ 0.1.

Fig. 2Correlation thermogram

4. Case analysis

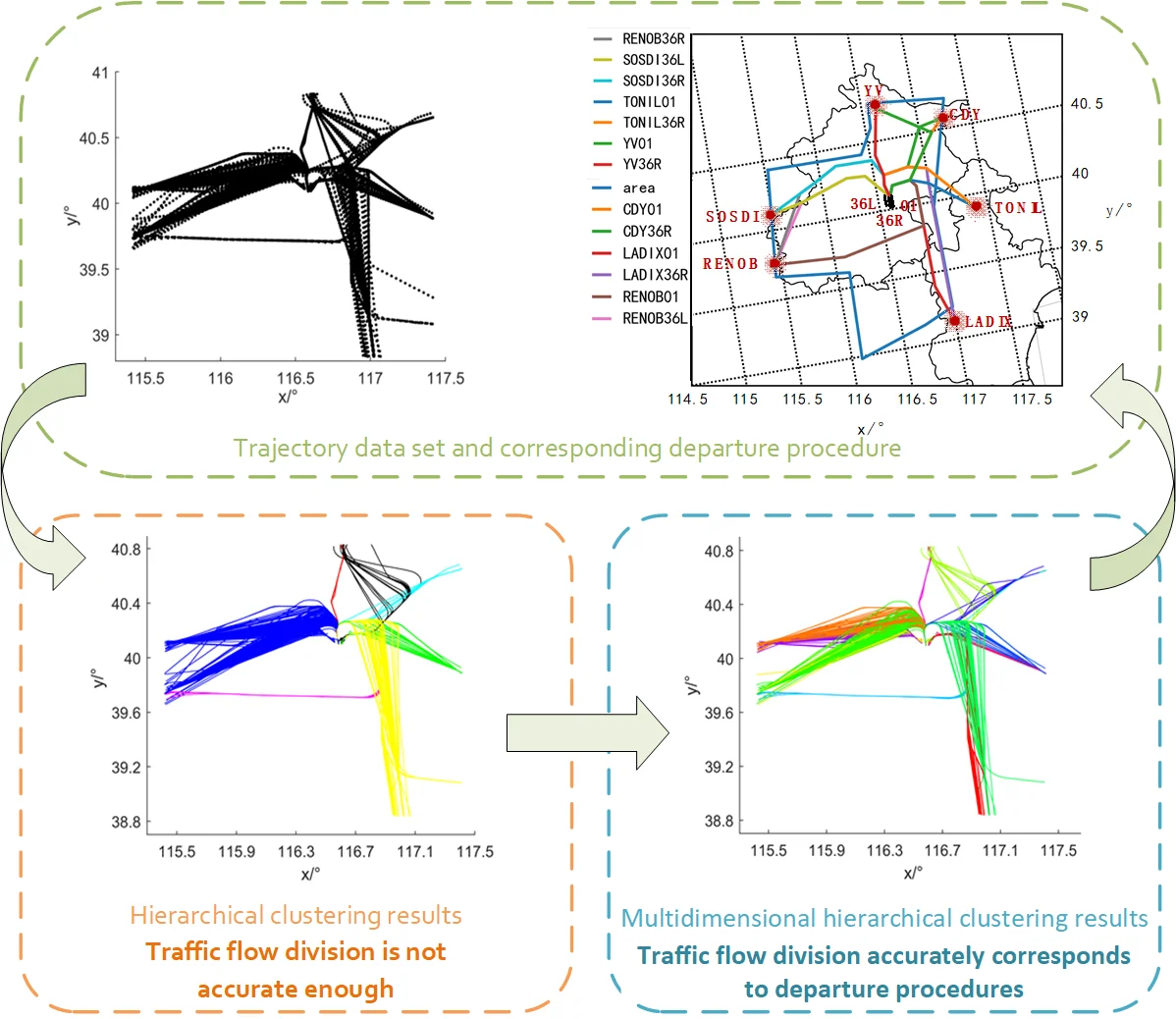
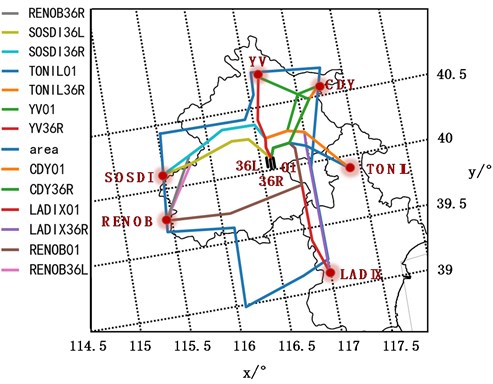
To verify the robustness of the algorithm and the accuracy of the algorithm, 703 radar trajectories, including 69763 data points, are selected as the input of the algorithm. The airport has three runways and six departure corridors. Flights in the terminal area of the airport basically follow regional area navigation (RNAV) procedures and radar guidance for departure flight. The map of 13 departure procedures used on the same day is shown in Fig. 3.

The minimum and maximum data points of a single trajectory in the trajectory set are 64 and 163 respectively. Set the number of resampling points to 50, adopt the method of equal arc length interpolation resampling, retain the first and last trajectory points, resample the trajectory set, and get a new flight trajectory set $G=\{P_1,P_2,\cdot \cdot \cdot ,P_i,\cdot \cdot \cdot ,P_m\}$. The resampling results are shown in Fig. 4. Compared with the off-site RNAV, the trajectory basically conforms to the program. The control points of different departure programs are different, the length of departure trajectory is different, and the time of departure program is also different. The multidimensional characteristics of the trajectory are resampled through the time series equal arc length interpolation, and the trajectory characteristics of different programs are retained. Therefore, it can be used as the input of the trajectory center extraction algorithm.

Fig. 3RNAV departure procedure

Some resampling data are shown in Table 1.

Fig. 5 shows DBI’s evaluation of clustering results with different number of clusters. The best number of clusters is 15, and the corresponding index value is 0.0967.

Fig. 4Terminal area off-site resampling

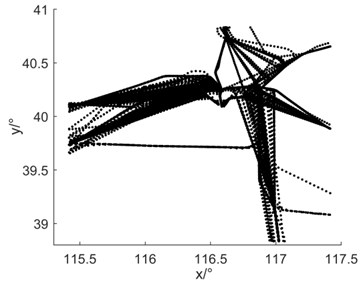
Fig. 5DBI curve

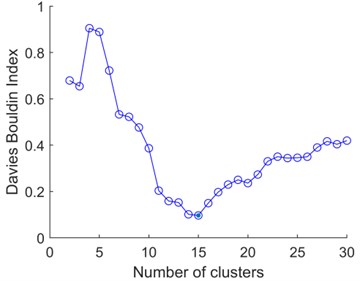
Fig. 6(a) is the experimental control group of traditional hierarchical clustering. The input of traditional hierarchical clustering is the Euclidean distance similarity matrix calculated by trajectory location feature, and the number of clusters needs to be manually specified as 15. Fig. 6(b) is the result of multidimensional hierarchical clustering. The traditional hierarchical clustering divides the 703 tracks into seven categories. The clustering does not distinguish between flights departing from different runways and westbound flights departing from SOSDI and RENOB. Therefore, the results cannot meet the requirements of extracting the center locus. Finally, 13 clusters of traffic flows are obtained by multidimensional hierarchical clustering, and the results can accurately correspond to 13 traffic flows from runway 36L, 36R and 01 to RENOB, SOSDI, YV, CDY, TONIL and LADIX. It is proved that the algorithm has strong robustness to complex operation scenarios.

Fig. 6The clustering results were compared with the 2D graph

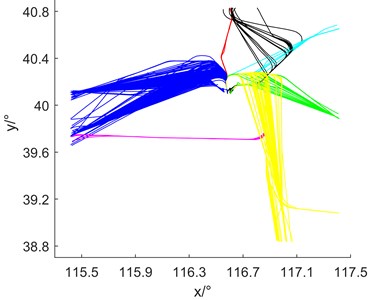
a) Hierarchical clustering results

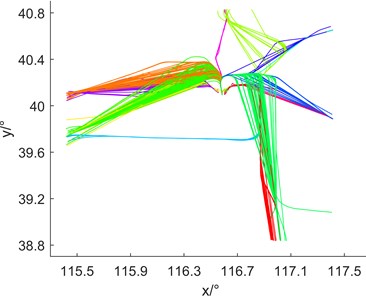
b) Multidimensional hierarchical clustering results

The experimental results were evaluated by using the cluster internal evaluation index, silhouette index (SI) and classification effect evaluation index, such as accuracy rate, recall rate and F1 score. The larger the SI is, the better the clustering result is. The accuracy rate is the proportion of the actual and correct trajectory in the correct classification and prediction of the algorithm; Recall rate is the proportion of the correct trajectories in the trajectory test set which are classified correctly by the algorithm; F1 score is the weighted harmonic average of accuracy and recall.

Table 2 shows the quantitative results of the experimental group and the control group. Compared with the traditional hierarchical clustering algorithm, the multidimensional hierarchical clustering algorithm is more adaptable and robust, because it does not need to specify the number of clusters in the way of manual input. And the application of multidimensional features makes full use of the ability to construct the details of trajectory features. On the one hand, it reduces the distance of trajectories in traffic flow, on the other hand, it increases the distance between traffic flows. It makes the contour coefficient of clustering increase and the F1 score increase.

Fig. 7 shows the results of multidimensional hierarchical clustering and the three-dimensional display of the center trajectory, respectively. the center trajectory is a smooth curve with multidimensional attributes such as time, space and speed, which is consistent with the actual flight. Compared with the clustering results, the trajectories extracted by the algorithm can correspond to the densest part of each traffic flow one by one, which directly proves the effectiveness of the algorithm.

Two departure programs with more trajectories are selected, which are 102 trajectories of SOSDI departure from runway 36R and 86 trajectories of RENOB departure, as shown in Fig. 8. the center trajectory extracted by this algorithm is the red line in the graph, which represents the densest trajectory of traffic flow. the characteristics of center trajectory include time, position, direction, velocity and climb gradient, which can use for abnormal trajectory recognition and initial trajectory input for trajectory prediction.

Fig. 73D diagram of experimental results

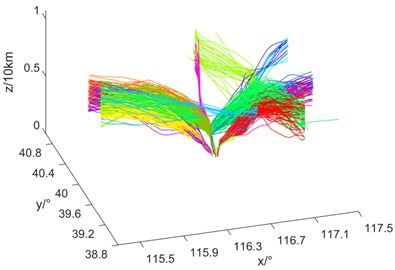
a) Traffic flows distribution

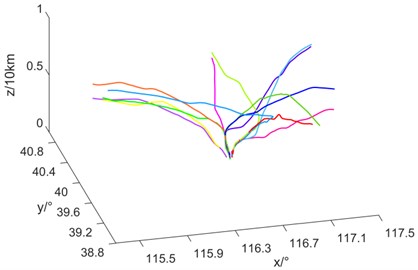
b) Central trajectories

Fig. 8Central trajectory in traffic flow

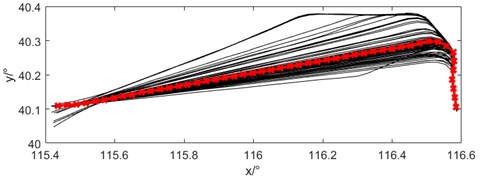
a) SOSDI36R departure

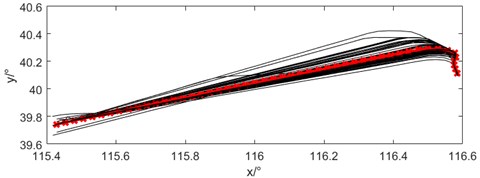
b) RENOB36R departure

5. Conclusions

This paper studies a center locus extraction algorithm based on multidimensional hierarchical clustering. It aims to make full use of the multidimensional features of the trajectory. the resampling of equal arc length interpolation preserves all the spatial and temporal characteristics of the trajectory accurately. Moreover, the weighted Euclidean distance increases the discrimination of traffic flow, making full use of the multidimensional trajectory’s characteristics. in a departure trajectory experiment at a large airport, the results show that the algorithm can obtain the traffic flow distribution and multidimensional feature center trajectory succinctly and efficiently by effectively reducing the data size from the complex operation scene. Thus, it provides a feasible method for aircraft trajectory prediction and a support for dynamic prediction of aircraft trajectory. Future research work includes optimizing multidimensional hierarchical clustering algorithms. and the center trajectory extraction results are compared with the standard departure procedures and quantitatively evaluated.