Abstract
In the coupling state of rotor unbalance fault and bearing defect fault for rotor system, the signals contain multiple fault components, and the fault diagnosis of the rotor system needs to contain comprehensive multidimensional feature quantities. However, irrelevant feature information in the multi-dimensional feature quantities increases the complexity of classification calculation and affects the efficiency and accuracy of diagnosis. In order to eliminate redundant and irrelevant features in the feature information, and achieve the goal of fewer diagnostic features and good diagnostic results, this paper proposes an adaptive feature selection based on the maximum information coefficient FF-FC-MIC (Feature-to-Feature and Feature-to-Category Maximum Information Coefficient) method. Firstly, the sparse representation algorithm is used to reconstruct the original signal to improve the signal-to-noise ratio, and the multi-dimensional feature quantity of the reconstructed signal is calculated; Secondly, calculate the correlation between features and features through MIC to obtain a feature set of weak correlation between features; thirdly, use MIC to calculate the correlation between features and signal categories to obtain a feature set with strong correlation between features and signals; Finally, the FF-FC-MIC feature selection method is used for feature adaptive selection and input into SVM to complete fault diagnosis. The method is analyzed by simulation signals and the real experiment signals. The results show that the method can effectively remove redundant and disclosed features in the coupling fault, reducing the characteristic dimension to reduce the fault classification time, and improve classification accuracy. Different experimental cases and various feature selection comparison methods further verify the accuracy and applicability of the proposed method.
Highlights
- Orthogonal Matching pursuit (OMP) sparse representation algorithm of adaptive Gabor sub-dictionary removes strong noise of coupling faults to highlight features.
- The FF-FC-MIC method innovatively and comprehensively considers the feature-feature correlation and feature-category correlation in fault signals to solve the adaptive selection of multidimensional features.
- FF-FC-MIC removes redundant features in coupling faults, reduces fault classification time and improves fault diagnosis rate.
- Simulation experiment and real experiment combined with SVM classification model are used to verify the superiority of the proposed method for coupling faults.
1. Introduction
Rotating machinery plays an important role in industrial production, and due to the nature of the working environment and full-time operation, its rotor system is a high incidence of mechanical failures. When the rotor system fails, the type of failure is prone to multiple failures and compound failures. For example, when the rotor has an unbalanced failure, the bearing will be damaged due to continuous impact; Similarly, when a bearing fails due to wear, impact, pitting, fatigue stress, etc., the resulting shock and vibration will adversely affect other parts and easily cause other parts to fail. Compared with a single fault signal, the signal of a compound fault is more complex, and the fault characteristics are difficult to extract. Therefore, the coupling fault diagnosis of the rotor system is of great significance [1-4].
Accurate and effective extraction of fault features is the key to fault diagnosis [5]. However, in the actual operation of the equipment, there are two problems in the feature separation and extraction of coupling faults: First, the signal components of coupling faults are more complex, and the signals of different faults affect each other, and the signal-to-noise ratio decreases, resulting in weak fault features being covered by noise components. As a result, it is difficult to extract fault features; The second is that the multi-dimensional feature quantities have feature quantities or redundant features that have nothing to do with the classification target, which affects the efficiency of fault diagnosis and reduces the accuracy of fault classification [6, 7].
The sparse representation method can characterize any signal as a superposition of a high-quality signal with structural features and a random noise signal, and can extract periodic structural features from a strong background noise environment to achieve sparse expression of the signal. For example, literature [8] proposed a latent component decomposition method based on sparse representation to realize the effective identification of weak fault characteristics of bearings and gears under strong noise background. Literature [9] Proposed a novel collaborative sparsity-assisted Fault Diagnosis (CSFD) method improves feature extraction capability and fault classification performance of rotor systems with strong noise. In the literature [10], the periodic weighted kurtosis sparse denoising is used and combined with the periodic filtering method to extract the repetitive pulses in the compound fault, so as to achieve the purpose of denoising and fault separation of the bearing compound fault signal. The sparse representation can be used to reconstruct the superposition of matched atoms into a high-quality signal with periodic structure characteristics in the signal [11]. Therefore, this paper chooses the sparse representation method for signal noise reduction.
Feature selection measures the correlation between features, removes redundant and irrelevant features from the feature set, improves the accuracy of fault diagnosis, and reduces the training time of the model. PCA was first applied to data dimension reduction, but it can only be used for linear relations between features, and is not suitable for complex nonlinear relations [12]. Compared with the traditional correlation coefficients of Pearson, Spearman, Kendall, etc. [13-15], MIC can capture a wide range of relationships when there are enough samples, instead of being limited to specific functional relationships, it has universality and uniformity [16]. Sun et al. [17] proposed a two-stage method of MIC and the approximate Markov blanket to measure the correlation between features and classes, remove redundant features, and select feature subsets. For complex mechanical fault diagnosis, reference [18] proposed a feature selection method that combined Fisher Score and MIC to evaluate the correlation between features to complete feature selection for gearbox faults.
To sum up, this paper proposes an adaptive feature selection method based on maximum information coefficient under sparse representation, which can comprehensively evaluate the correlation of features to features and features to categories. Firstly, in order to solve the empirical selection of parameters in sparse representation, the multi-step grid search method of parameter optimization is used to complete the reconstruction of the signal, and the multi-dimensional feature quantity of the reconstructed signal is calculated; Secondly, the maximum information coefficient MIC is used to calculate the correlation between features and features and between features and signal categories to filter out redundant and irrelevant features; Finally, the FF-FC-MIC adaptive feature selection method is used to complete the feature selection and input to SVM for fault diagnosis.
The main contributions of this paper can be summarized as follows:
1) Orthogonal Matching pursuit (OMP) sparse representation algorithm of adaptive Gabor sub-dictionary removes strong noise of coupling faults to highlight features.
2) The FF-FC-MIC method innovatively and comprehensively considers the feature-feature correlation and feature-category correlation in fault signals to solve the adaptive selection of multidimensional features.
3) FF-FC-MIC removes redundant features in coupling faults, reduces fault classification time and improves fault diagnosis rate.
4) Simulation experiment and real experiment combined with SVM classification model are used to verify the superiority of the proposed method for coupling faults.
Arrangements for other parts of the paper are as follows: Section 2 introduces the theoretical background of the method, including sparse representation and feature selection method based on maximum information coefficient. Section 3 describes the whole diagnostic process of the proposed method for the coupling failure of the rotor system. Section 4 consists of two parts: simulation experiment and real experiment. The feasibility of the method is preliminarily verified by simulation coupling signal, and the actual experiment is verified by three real cases and compared with other methods. Section 5 is the summary of the paper and the prospect of the future work.
2. Methodology
2.1. Sparse representation
Assuming that the signal is and its length is , it can be regarded as a vector of , the redundant dictionary , where , the signal y can be expressed as the computational superposition of the basis function as shown in Eq. (1):
where is the coefficient of the basis function, and is the sparse representation of the signal.
The sparse representation method adopted in this paper is the adaptive Gabor sub-dictionary Orthogonal Matching Pursuit (OMP) algorithm. Gabor atom is a kind of time – frequency atom and has good time-frequency approximation performance. It has a good tracking effect on the stationary components in the signal and can match the cyclic characteristics in the signal. Eq. (2) is the basic definition:
where, is the Gaussian window function; is the atomic parameter; is the scale factor; is the displacement factor; is the frequency factor. Let be the Fourier transform of , then the Fourier transform of Gabor atom can be obtained according to Eq. (1), as shown in Eq. (3):
The calculation process of OMP is to build the over-complete dictionary of Gabor atom through the original signal, and use OMP algorithm to match the original signal, find the best matching atom in the over-complete dictionary and generate the residual signal. A new over-complete dictionary is generated according to the residual signal and the next matching calculation is performed until the residual signal meets the shutdown condition [19].
2.2. MIC
The calculation of MIC is based on the concept of mutual information and meshing method of information theory [20]. Mutual information is used to measure the correlation between two variables. Let , , represent the number of samples, and the mutual information between and is defined as Eq. (4):
where, is the joint probability density of and . and are the edge probability density of and respectively.
When MIC based on the concept of mutual information is calculated, the set of two data points is distributed in two-dimensional space. is defined as grid of size , where the range of is divided into segment and the range of is divided into segment , and the limit of the grid is , . The maximum value of mutual information between variable and variable in different meshes is calculated and called maximum mutual information. Eq. (5-6) are the definition formula and calculation formula of maximum mutual information respectively:
where and are the number of cells divided on the range and , respectively. is the mutual information of variable and variable .
2.3. Adaptive feature selection method based on MIC
Traditional feature selection only relies on calculating the correlation between features to remove redundant features without considering the signal-independent features. MIC can not only measure the correlation between features and features, but also between features and signal categories [21]. In order to reduce the complexity of the classification calculation caused by the irrelevant feature information in the multi-dimensional feature quantity, this paper proposes the FF-FC-MIC method to realize the adaptive feature selection of the coupled fault multi-dimensional information. Firstly, calculate the MIC between the feature and the feature, select the irrelevant feature of the feature and the feature in order to eliminate the redundant features; secondly, calculate the MIC between the feature and the signal category, and get the feature based on the strong correlation between the feature and the signal category. Finally, the features obtained by the two methods are intersected, and the feature intersection is the final feature set for classification.
According to the FF-MIC feature selection method, the correlation between features is calculated and the uncorrelated features are selected. kinds of signals whose signal category is are set. -dimensional features are selected for each type of signals, and the complete set of features is . The maximum information coefficient between a feature of a single signal and other features is calculated as shown in Eq. (7-8), where is the serial number of each feature:
where is the serial number of each feature.
According to Eq. (1) and Eq. (2), the maximum information coefficients between different eigenvalues of signals are calculated and listed as FF-MIC matrix:
Select the minimum value of each column in the FF-MIC matrix, and all the minimum values form the set , and then set the maximum value in this set as the threshold :
The elements in each column of matrix FF-MIC are compared with the threshold value , and the number of elements in each column less than the threshold value is set to to form the set . The more elements in each column are less than the threshold value, the weaker the correlation between the column features and other features is. The average of the number of elements in each column that are below the threshold is calculated, and features that are greater than the average are selected:
where, is the set of elements in each column less than the threshold , and is the average value of elements in each column less than the threshold.
All the selected features are composed into a set , where is the selected feature, is the serial number of each selected feature, is the number of the selected feature, :
Multiple types of signals are classified, the selected feature sets of each type of signals are calculated respectively, and the feature sets obtained by all signals are combined to form the feature matrix , :
Fig. 1Correlation between feature and signal category
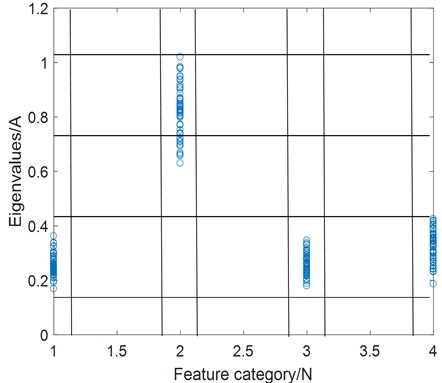
The feature selection method based on FC-MIC selects features with strong correlation between features and signal categories by calculating the correlation between features and signal categories. Establish the feature selection process as shown in Fig. 1, where the -axis represents the fault category (category is represented by a number), and the -axis represents the size of the eigenvalue of all samples if the sample type is the value of the -axis. The maximum system information coefficients between features and signal categories are calculated, and the FC-MIC matrix with size of is obtained:
The average value of all MIC is calculated as the threshold value , and those greater than the average value are strongly correlated features, which are selected. All strongly correlated features are formed into an eigenmatrix , and is the number of selected features, :
where is the number of selected features, .
According to two parallel feature selection methods, eigenmatrices and are obtained. Then find the intersection of and to obtain the feature subset as shown in Eq. (20):
3. The framework of fault diagnosis based on FF-FC-MIC
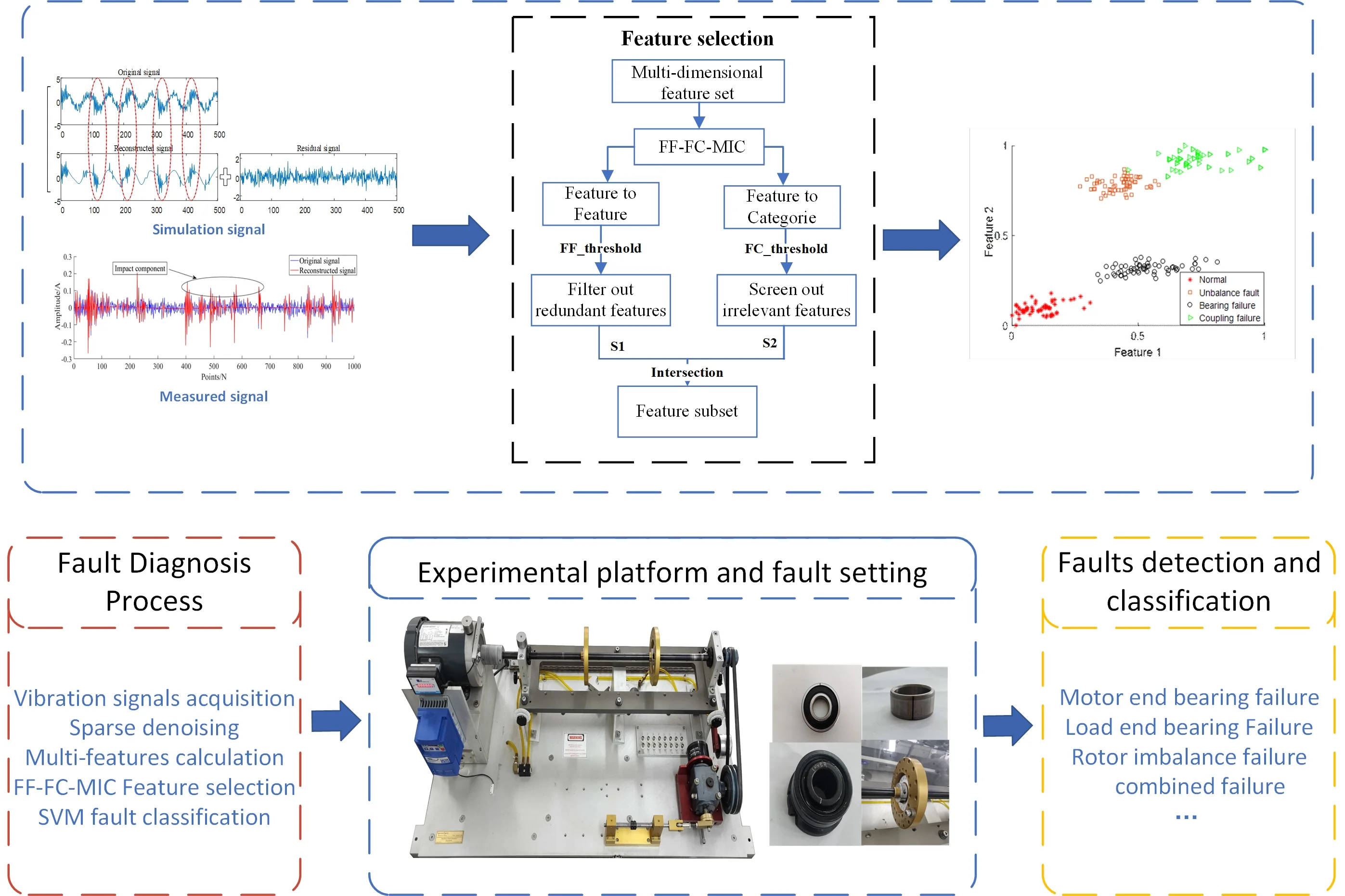
Different fault components in a coupled fault affect each other, a single feature quantity cannot satisfy the diagnosis and recognition of a coupled fault, and the multi-dimensional feature quantity contains irrelevant feature information that will affect the efficiency and accuracy of the diagnosis. To solve the above problems, this paper proposes an adaptive feature selection method based on the maximum information coefficient. The technical route is shown in Fig. 2.
Fig. 2Fault diagnosis process based on FF-FC-MIC feature selection
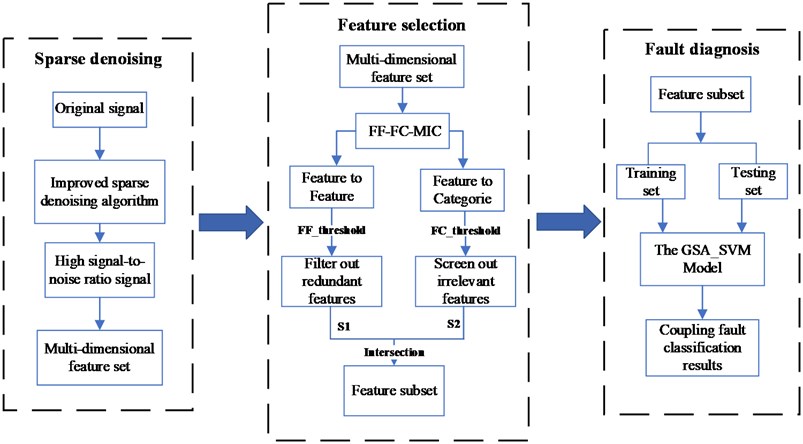
(1) Use the multi-step grid search method to optimize the displacement factor and frequency factor of the Gabor atomic dictionary to improve the noise reduction ability and computing efficiency of the sparse representation algorithm.
(2) Use the sparse representation algorithm of step (1) to decompose and reconstruct the original signal to reduce the noise interference of the coupled fault signal.
(3) Calculate the correlation between features and features through MIC, and obtain a set of weak correlation features between features to eliminate redundant features of multi-dimensional information.
(4) Calculate the correlation between features and signal categories through MIC to obtain a set of strong correlation features between features and signals, and eliminate irrelevant features.
(5) The FF-FC-MIC feature selection method is proposed for feature adaptive selection, and the selected features are input into SVM to complete the classification and identification of coupling faults.
4. Experiment
4.1. Experimental simulation analysis
In this section, the effect of the proposed method is preliminarily verified by constructing simulation signals:
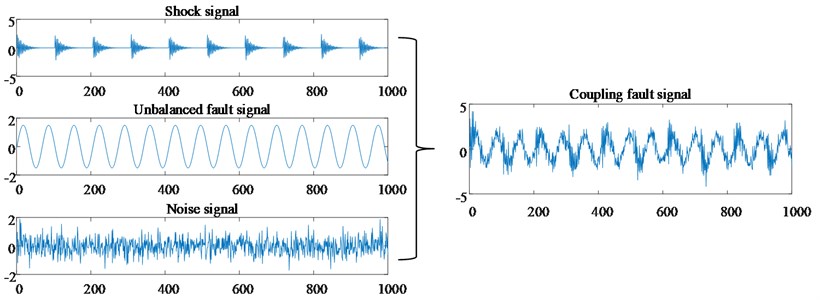
As shown in Eqs. (21-24), bearing normal, single bearing fault, single unbalance fault and unbalanced-bearing coupling fault are simulated respectively, where represents Gaussian white noise signal. Simulate these four kinds of signals each with 60 groups, a total of 240 groups, of which 30 groups of data are selected as training samples for each signal, and 30 groups of data are used as test samples. Fig. 3 shows the imbalance-bearing coupling fault simulation signal and its signal composition. The improved sparse denoising algorithm is used to preprocess the simulated coupling fault signal and obtain the reconstructed signal with high SNR, as shown in Fig. 4.
Fig. 3Simulation signal of coupling fault
Next, Multi-class features of reconstructed signals are required, including 14 dimensional features such as time domain feature, frequency domain feature and entropy value feature. Table 1 describes the detailed information of these features. Finally, use SVM for classification, use radial basis kernel function (RBF) as the kernel function, and optimize the parameters of SVM using grid optimization algorithm. Fig. 5 shows the fault classification under the one-dimensional feature when the feature is the root mean square. Fig. 6 shows the fault classification situation under the two-dimensional feature when the features are the root mean square value and kurtosis.
Fig. 4Coupling fault based on sparse denoising reconstruction signal
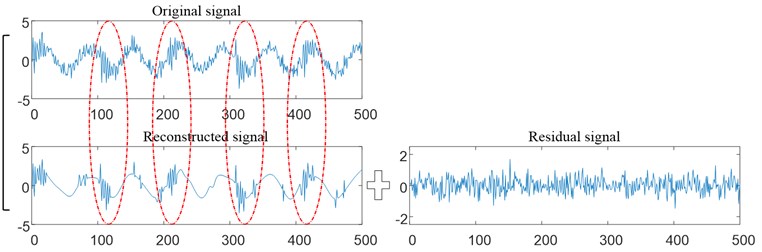
Table 1Types of feature quantities
Features of the type | Features |
Time-domain feature | 1-peak-to-peak index 2-RMS 3-Kurtosis index 4-Peak index 5-Waveform index 6-Impulsion index 7-Tolerance index |
Frequency-domain feature | 8-Center frequency 9-Variance frequency 10-Mean square frequency (MSF) 11-RMS frequency |
Entropy feature | 12-Singular spectrum entropy 13-Power spectral entropy 14-scale entropy |
Fig. 5Fault classification under one-dimensional characteristics of the simulated signal
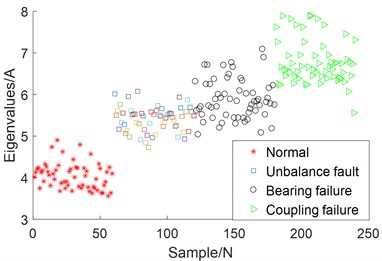
Fig. 6Fault classification under two-dimensional characteristics of the simulated signal
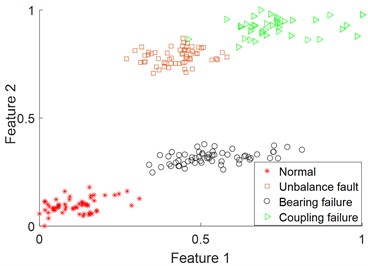
By comparing Fig. 5 and Fig. 6, it can be seen that the effect of fault classification using two-dimensional feature is higher than that using one-dimensional single feature. It shows that the multi-dimensional features of coupling faults express more comprehensive information, so the classification effect is higher than that of single-dimensional features. But which feature vectors to select for fault classification is a problem.
The FF-FC-MIC method proposed in this paper is used to select suitable features. First, feature ordinals with high correlation between feature-feature and feature-category are selected by FF-MIC and FC-MIC methods respectively, and then the intersection of these ordinals is calculated. The result of feature selection is shown in Table 2. Five features are selected using FF-FC-MIC, and the signal features are represented by numbers 1-14.
Table 2Simulation signal feature selection results
Selecting features number | FF-FC-MIC | |
FF-MIC | 1, 2, 4, 5, 6, 7, 8, 9, 12, 13, 14 | 2, 5, 9, 12, 13 |
FC-MIC | 2, 3, 5, 9, 10, 11, 12, 13 |
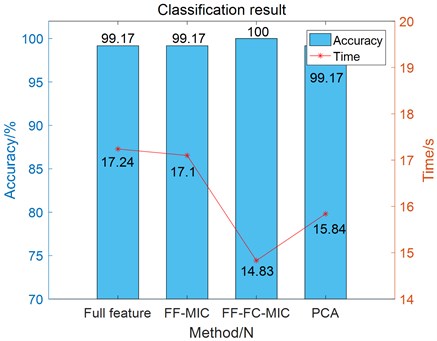
The five types of features selected by FF-FC-MIC are input into SVM for fault diagnosis. At the same time, the effects of FF-MIC method, principal component analysis (PCA) and this method are compared. The results of the full feature classification without feature selection and the classification effects of the three feature selection methods are shown in Fig. 7. It can be seen from Fig. 7 that the classification accuracy of the FF-FC-MIC feature selection method proposed in this paper is up to 100 %, and the shortest time to complete the classification is only 14.83 s. The simulation experiment analysis proves that this method not only improves the accuracy of fault classification, but also reduces the time of fault classification.
Fig. 7Simulation signal classification accuracy
4.2. Real experimental signal analysis
In order to analyze and verify the proposed method, a rotor system was simulated by SQ company's mechanical fault comprehensive test bench. The rotor unbalance fault, load end bearing fault, motor end bearing fault and their coupling faults are simulated respectively by using the test bed. Fig. 8 shows the structure composition and fault setting of the experimental platform. The bearings used in the experiment were load bearing of Type ER-12K and motor bearing of type 6203, and the unbalanced mass was composed of a screw and two gaskets mounted on the wheel. In the experiment, the motor speed was set at 1800 r/min and the sampling frequency was set at 12800 Hz. The vibration signal in this paper was collected by acceleration sensor B.
Fig. 8Test bench structure diagram and faults setting


Table 3Details of the coupling failure set up in the experiment
Case | Coupling fault information of signals |
Case 1 | Unbalance – Inner ring of load bearing (U-IL) Unbalance – Rolling body of load bearing (U-RL) Unbalance – Inner ring of motor bearing (U-IM) Unbalance – Rolling body of motor bearing (U-IM) |
Case 2 | Inner ring of motor bearing – Inner ring of load bearing (IM-IL) Inner ring of motor bearing – Outer ring of load bearing (IM-OL) Outer ring of motor bearing – Inner ring of load bearing (OM-IL) Outer ring of motor bearing – Outer ring of load bearing (OM-OL) |
Case 3 | Unbalance (U) Inner ring of motor bearing (IM) Unbalance – Inner ring of motor bearing (U-IM) Inner ring of motor bearing – Inner ring of load bearing (IM-IL) |
Three experimental cases were used to verify the method proposed in this paper, and each case was composed of signals of four different fault types. The detailed information of signal fault types in the three experimental cases is shown in Table 3. The fault signal types in case 1 are coupling faults between rotor unbalance and bearings; Case 2 is the coupling fault signal between motor bearing and load bearing; Case 3 includes single rotor unbalance fault, single bearing fault, unbalance – bearing coupling fault, and bearing – bearing coupling fault. 240 groups of signals were collected for each experimental case, including 60 groups of each type of fault signal (30 groups of training samples, 30 groups of test samples).
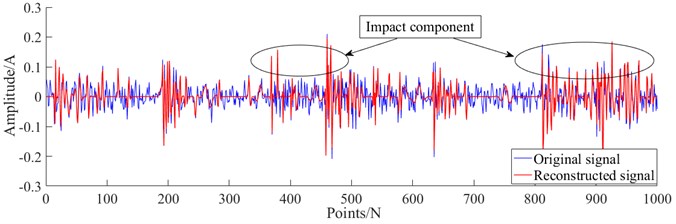
The coupling fault signal in case 1 is analyzed experimentally using the method proposed in this paper. Firstly, denoising preprocessing was performed on the collected multi-type coupling fault signals, using the improved sparse representation algorithm mentioned in this paper. Fig. 9-12 show the reconstructed signals after denoising. It can be seen from Fig. 9-12 that the reconstructed signal ensures the useful impact features in the original signal while removing the useless features in the signal.
Fig. 9The reconstructed signal of coupling fault U-IL
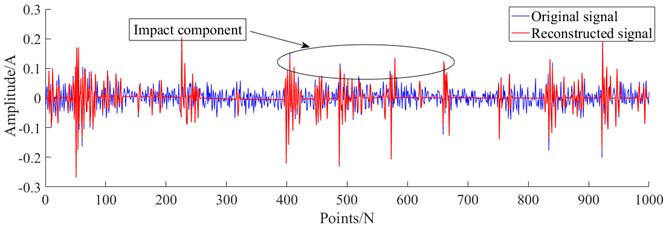
Fig. 10The reconstructed signal of coupling fault U-RL
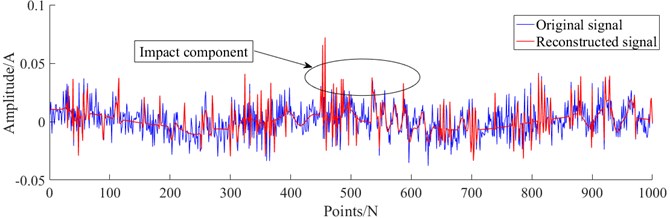
Fig. 11The reconstructed signal of coupling fault U-IM
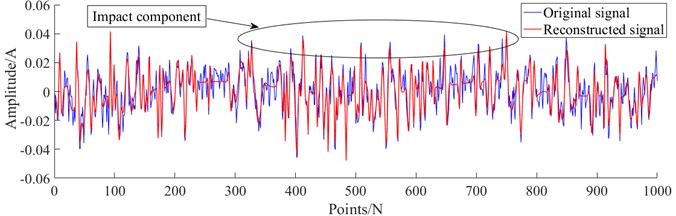
Fig. 12The reconstructed signal of coupling fault IM-IL
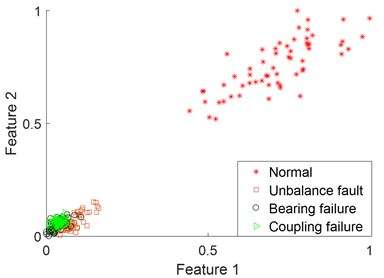
Similarly, 14 feature vectors of 14 dimensions were calculated by using 14 feature indexes mentioned in the simulation experiment, and fault classification was analyzed by combining SVM. Fig. 13 shows the fault classification results under one-dimensional single feature vector, and Fig. 14 shows the fault classification results under two-dimensional feature. As can be seen from Fig. 13 and 14, for complex coupled faults, the fault classification effect of single feature vector and randomly selected low-dimensional feature vector is very poor.
Fig. 13Fault classification under the one-dimensional feature of the actual signals
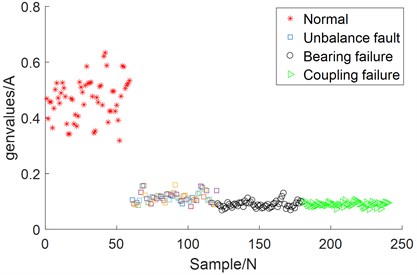
Fig. 14Fault classification under the two-dimensional feature of the actual signals
Furthermore, the FF-FC-MIC method proposed in this paper is used for adaptive feature selection of coupling faults. The results of FF-FC-MIC feature selection for two different experimental cases are shown in Table 4. For the coupling fault signals between unbalance and bearings in case 1, FF-FC-MIC adaptively selects 4 types of features. For coupling fault signals between motor bearings and load bearings in Case 2, FF-FC-MIC selects 8 types of features. And for coupling fault signals and single fault signal in Case 3, FF-FC-MIC selects 6 types of features. Then the selected feature vectors are input into the SVM model for fault classification.
Table 4Coupling fault adaptive feature selection results
Case | Selecting features number | |
Case 1 | FF-FC-MIC | 2, 5, 11, 12 |
Case 2 | FF-FC-MIC | 1, 2, 3, 5, 6, 11, 12, 14 |
Case 3 | FF-FC-MIC | 2, 5, 6, 11, 12, 14 |
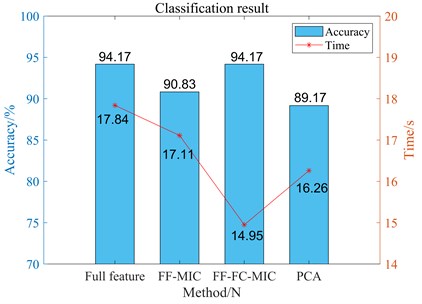
Fig. 15 shows the classification results of unbalanced-bearing coupling fault signals in case1, which are selected by different feature selection methods and then classified by SVM model. It can be seen from Fig. 15 that the classification accuracy of the 4-dimensional features selected by FF-FC-MIC in case 1 is 94.17 %, and the classification time is only 14.95 s. In addition, PCA and FF-MIC feature selection methods as well as full features not selected by feature selection were used for comparative analysis, as shown in Fig. 15. Compared with the full-feature method without feature selection, although the classification accuracy is the same, the classification time of ff-FC-MIC method is significantly reduced due to the removal of useless features after feature selection. And compared with other two feature selection methods, FF-FC-MIC has great advantages in ensuring accuracy and reducing classification time for unbalanced-bearing coupling faults.
Fig. 15Classification effects of different feature selection methods on case1 coupling faults
Case 2 is aimed at the coupling fault of motor bearing-load bearing, and Fig. 16 shows the fault classification results of different feature selection methods. According to the comparison in Fig. 16, while FF-FC-MIC is equal to the other three methods in classification time, it greatly improves the accuracy of SVM classification. Case 3 integrated single fault and coupling fault in rotor system. Fig. 17 is the comparison of classification accuracy and classification time of case 3 using this method and other three methods. It can be seen from Fig. 17 that this method still has obvious advantages in classification accuracy and time in this case.
Fig. 16Classification effects of different feature selection methods on case 2 coupling faults
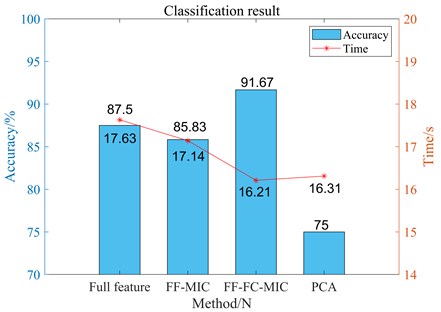
Fig. 17Classification effects of different feature selection methods on case 3
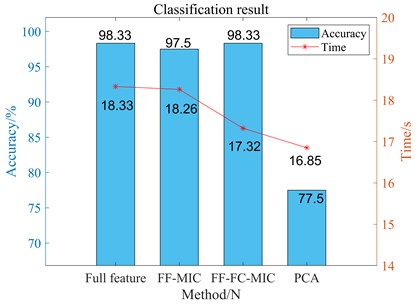
In the above analysis of three real cases of rotor system faults, the method proposed in this paper has excellent classification results compared with other methods. Experimental results show that this method can not only improve the accuracy of fault classification but also reduce the time of fault classification. Case 1 and Case 2 mainly deal with the applicability of this method when complex coupling faults exist in the rotor system. Case 3 includes single faults and coupled faults, but the classification effect still reaches 98.33 %. The three experiments show that the proposed method has excellent performance in fault diagnosis of the rotor system.
5. Conclusion
Aiming at the problem that the features extracted from composite fault signals of bearings contain redundant and irrelevant features, this paper proposes a diagnosis method based on MIC adaptive feature selection. According to the above-mentioned simulation experiment analysis and actual signal experiment analysis, the superiority of the FF-FC-MIC feature selection method proposed in this paper is verified. In the simulation experiment, due to the obvious fault characteristics of the simulation, the use of single or low-dimensional feature quantities can also have a better fault classification effect. However, in the actual measurement of complex coupling fault classification of the signal, due to the mutual interference between the characteristics of the coupling fault, the use of a single feature quantity or random low-dimensional feature quantity cannot achieve a better fault classification effect. Two sets of experiments on measured signals show that the FF-FC-MIC feature selection method can adaptively select multi-dimensional feature quantities, effectively eliminating redundant and irrelevant features. Comparing the method proposed in this paper with other feature selection methods, it is proved that this method improves the classification accuracy of coupled fault diagnosis, reduces the time of fault classification, and verifies the effectiveness and practicability of the method.
1) The proposed method effectively removes redundant features and irrelevant features from the coupled fault feature information, reduces the feature dimension and reduces the time of fault classification.
2) The proposed method improves the accuracy of classification while reducing the feature dimension, which proves the superiority of the algorithm.
In the future, we hope to transfer this adaptive feature selection method to residual life prediction of machinery. It is well known that the selection of suitable features is the premise of life prediction research, but the current research methods are based on experience or complex multiple attempts to select suitable features, and the selection is not necessarily the optimal feature. It is expected to contribute to the research of residual life prediction in the future.
References
-
P. M. Jadhav, S. G. Kumbhar, R. G. Desavale, and S. B. Patil, “Distributed fault diagnosis of rotor-bearing system using dimensional analysis and experimental methods,” Measurement, Vol. 166, p. 108239, Dec. 2020, https://doi.org/10.1016/j.measurement.2020.108239
-
W. Huang et al., “Multi-source fidelity sparse representation via convex optimization for gearbox compound fault diagnosis,” Journal of Sound and Vibration, Vol. 496, p. 115879, Mar. 2021, https://doi.org/10.1016/j.jsv.2020.115879
-
Z. Yi, N. Pan, and Y. Guo, “Mechanical compound faults extraction based on improved frequency domain blind deconvolution algorithm,” Mechanical Systems and Signal Processing, Vol. 113, pp. 180–188, Dec. 2018, https://doi.org/10.1016/j.ymssp.2017.06.028
-
Sun R. B. et al., “Sparse representation based on parametric impulsive dictionary design for bearing fault diagnosis,” Mechanical systems and signal processing, Vol. 122, pp. 737–753, 2019.
-
Y. Du, A. Wang, S. Wang, B. He, and G. Meng, “Fault diagnosis under variable working conditions based on STFT and transfer deep residual network,” Shock and Vibration, Vol. 2020, pp. 1–18, May 2020, https://doi.org/10.1155/2020/1274380
-
L. Wang and Y. Shao, “Fault feature extraction of rotating machinery using a reweighted complete ensemble empirical mode decomposition with adaptive noise and demodulation analysis,” Mechanical Systems and Signal Processing, Vol. 138, p. 106545, Apr. 2020, https://doi.org/10.1016/j.ymssp.2019.106545
-
J. Guo, D. Zhen, H. Li, Z. Shi, F. Gu, and A. D. Ball, “Fault feature extraction for rolling element bearing diagnosis based on a multi-stage noise reduction method,” Measurement, Vol. 139, pp. 226–235, Jun. 2019, https://doi.org/10.1016/j.measurement.2019.02.072
-
H. Tang, J. Chen, and G. Dong, “Sparse representation based latent components analysis for machinery weak fault detection,” Mechanical Systems and Signal Processing, Vol. 46, No. 2, pp. 373–388, Jun. 2014, https://doi.org/10.1016/j.ymssp.2014.01.011
-
Y. Niu and J. Fei, “A Sparsity-assisted fault diagnosis method based on nonconvex sparse regularization,” IEEE Access, Vol. 9, No. 99, pp. 59027–59037, 2021, https://doi.org/10.1109/access.2021.3073072
-
J. Meng, H. Wang, L. Zhao, and R. Yan, “Compound fault diagnosis of rolling bearing using PWK-sparse denoising and periodicity filtering,” Measurement, Vol. 181, p. 109604, Aug. 2021, https://doi.org/10.1016/j.measurement.2021.109604
-
R. G. Baraniuk, E. Candes, M. Elad, and Yi Ma, “Applications of sparse representation and compressive sensing [Scanning the Issue],” Proceedings of the IEEE, Vol. 98, No. 6, pp. 906–909, Jun. 2010, https://doi.org/10.1109/jproc.2010.2047424
-
H. M. Genc, Z. Cataltepe, and T. Pearson, “A new PCA/ICA based feature selection method,” in 2007 15th IEEE Signal Processing and Communications Applications, Jun. 2007, https://doi.org/10.1109/siu.2007.4298772
-
H. Zhou, Z. Deng, Y. Xia, and M. Fu, “A new sampling method in particle filter based on Pearson correlation coefficient,” Neurocomputing, Vol. 216, pp. 208–215, Dec. 2016, https://doi.org/10.1016/j.neucom.2016.07.036
-
M.-T. Puth, M. Neuhäuser, and G. D. Ruxton, “Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits,” Animal Behaviour, Vol. 102, pp. 77–84, Feb. 2017.
-
E. Liebscher, “Kendall regression coefficient,” Computational Statistics and Data Analysis, Vol. 157, p. 107140, May 2021, https://doi.org/10.1016/j.csda.2020.107140
-
S. Zhang, X. Guo, X. Dou, and X. Zhang, “A data-driven coulomb counting method for state of charge calibration and estimation of lithium-ion battery,” Sustainable Energy Technologies and Assessments, Vol. 40, p. 100752, Aug. 2020, https://doi.org/10.1016/j.seta.2020.100752
-
G.-L. Sun, Z.-C. Song, J.-L. Liu, S.-X. Zhu, and Y.-J. He, “Feature selection method based on maximum information coefficient and approximate markov blanket,” Zidonghua Xuebao/Acta Automatica Sinica, Vol. 43, No. 5, pp. 795–805, May 2017, https://doi.org/10.16383/j.aas.2017.c150851
-
Zhao Ling et al., “Fault feature selection method of gearbox based on fisher score and maximum information coefficient,” (in Chinese), Control and Decision, Vol. 36, No. 9, Sep. 2021, https://doi.org/10.13195/j.kzyjc.2019.1770
-
Liu Z. and Wu X. J., “Sparsity augmented discriminative sparse representation for face recognition,” Pattern Analysis and Applications, Vol. 22, No. 4, p. 1527, 2019.
-
S. Wang, Y. Zhao, Y. Shu, H. Yuan, J. Geng, and S. Wang, “Fast search local extremum for maximal information coefficient (MIC),” Journal of Computational and Applied Mathematics, Vol. 327, pp. 372–387, Jan. 2018, https://doi.org/10.1016/j.cam.2017.05.038
-
L. Wang, S. Jiang, and S. Jiang, “A feature selection method via analysis of relevance, redundancy, and interaction,” Expert Systems with Applications, Vol. 183, p. 115365, Nov. 2021, https://doi.org/10.1016/j.eswa.2021.115365
About this article
This work was supported in part by the National Nature Science Foundation of China under Grant U1804141, in part by Foundation for University Key Teacher of Henan Educational Department (No. 2018GGJS091), and in part by Science and Technology Program of Henan, China (No. 222102220081).
