Optimal design parameters of air suspension systems for semi-trailer truck. Part 1: modeling and algorithm

1. Introduction

Vehicle’s air suspension is an important component to reduce the dynamic wheel load acting on the road surface as well as improve the riding comfort. The influences of vehicle parameters as well as operating conditions on the dynamic load of the wheels were considered and analyzed by using the 3D vehicle-pavement coupled model [1]. The effects of vehicle suspension parameters and operating conditions on the safety of vehicle movement and the durability of vehicle parts were analyzed by using the 3D nonlinear dynamic model [2]. To analyze the ride performances of the air or hydro-pneumatic suspension systems, the 3D dynamic model with 14 d.o.f. was developed to compare the ride performance of two suspension systems: the traditional and new air spring of suspension systems for a semi-trailer truck [3], the dynamic model of quarter vehicle with 2 d.o.f. was established to compare the ride performance of two suspension system models: classic air spring and dynamic air spring models [4], and the 3D dynamic model with 15 d.o.f. was used to analyze the ride performance of the hydro-pneumatic suspension system compared to the rubber and air spring suspension systems [5]. To improve the ride performance of the suspension system for vehicle, many optimal techniques have been used in various fields of study to design vehicle passive suspension systems. The parameters of the suspension systems using vehicle dynamic model with 2 d.o.f. are optimized to improve the friendly road surface and vehicle ride comfort [6]. Suspension parameters are optimized by using genetic algorithm (GA) [7, 9], multi-objective genetic algorithm (MOGA) (such as NSGA-II, SPEA2 and PESA-II) [8], multi-objective uniform-diversity genetic algorithm (MUGA) with a diversity preserving mechanism [10]. The goal of this paper is to establish a half-vehicle dynamic model for finding the optimal design parameters of air spring and air suspension. The classical nonlinear dynamic model of an air spring suspension system is established for identifying the parameters of the proposed air spring model. The target function and the constraints are proposed with two optimal cases. The results of Part 1 in this paper provide a theoretical basis for Part 2 as the results and discussion.

2. Vehicle dynamic model

2.1. Half-vehicle dynamic model

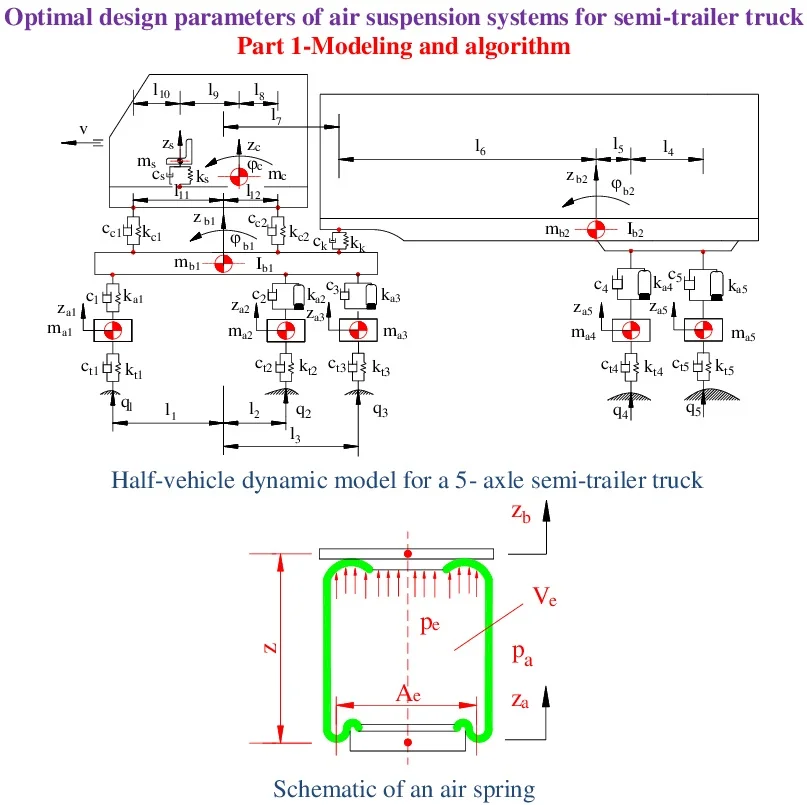
A semi-tractor-trailer truck with a dependent leaf spring of suspension system for the front steer axle and four air spring of suspension systems for the rear axles of tractor and trailer is selected for vehicle dynamic analysis and optimum. A half- vehicle dynamic model for a 5-axle semi-trailer truck [12, 17] was established to search the optimal parameters of air spring of suspension systems and air suspension systems, as shown in Fig. 1.

Fig. 1Half-vehicle dynamic model for a 5-axle semi-trailer truck

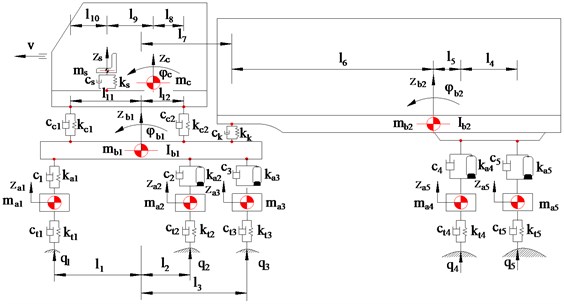
In Fig. 1, $m_{a1}$, $m_{a2}$ and $m_{a3}$ are the wheel masses of the tractor axles, respectively; $m_{a4}$and $m_{a5}$ are the wheel masses of the attached trailer axles; $m_{b1}$, $m_{b2}$, $m_c$ and $m_s$ are the masses of the tractor body, trailer body, cab body, and driver seat, respectively; $I_{b1}$, $I_{b2}$ and $I_c$ are the mass moment of inertia about the pitch axis of the tractor body, trailer body and cab body; $l_k$ are the calculation distances; $k_{t1}$, $k_{t2}$, $k_{t3}$, $k_{t4}$, $k_{t5}$ and $c_{t1}$, $c_{t2}$, $c_{t3}$, $c_{t4}$, $c_{t5}$ are the tire stiffness and damping coefficients, respectively; $k_{a1}$, $k_{a2}$, $k_{a3}$, $k_{a4}$, $k_{a5}$ and $c_1$, $c_2$, $c_3$, $c_4$, $c_5$ are the vehicle suspension stiffness and damping coefficients, respectively; $k_{c1}$, $k_{c2}$ and $c_{c1}$, $c_{c2}$ are the cab suspension stiffness and damping coefficients, respectively; $k_s$ and $c_s$ are the driver seat stiffness and damping coefficients; $z_{a1}$, $z_{a2}$, $z_{a3}$, $z_{a4}$ and $z_{a5}$ are the vertical body displacement of the axles, respectively; $z_{b1}$ an $z_{b2}$ are the vertical body displacement of the tractor and trailer; $z_c$ is the vertical body displacement of cab; $z_s$ is the vertical body displacement of driver seat, respectively;${\phi }_{b1}$ and ${\phi }_{b2}$ are the pitch response of the tractor and trailer; ${\phi }_c$ is the pitch response of cab; v is the vehicle speed ($k=$1-10).

From the half-vehicle dynamic model for a 5-axle semi-trailer truck, as shown in Fig. 1. The differential equations describing the motion of the masses of the axles, tractor body, trailer body, cab body, and driver seat using Lagrange equations of type II are written below:

1

$m_{a1}{\ddot{z}}_{a1}=\left[k_1\left(z_{b1}-l_1{\phi }_{b1}-z_{a1}\right)+c_1\left({\dot{z}}_{b1}-l_1{\dot{\phi }}_{b1}-{\dot{z}}_{a1}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{t1}\left(z_{a1}-q_1\right)+c_{t1}\left({\dot{z}}_{a1}-{\dot{q}}_1\right)\right],$

2

$m_{a2}{\ddot{z}}_{a2}=\left[k_{a2}\left(z_{b1}+l_2{\phi }_{b1}-z_{a2}\right)+c_2\left({\dot{z}}_{b1}+l_2{\dot{\phi }}_{b1}-{\dot{z}}_{a2}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{t2}\left(z_{a2}-q_2\right)+c_{t2}\left({\dot{z}}_{a2}-{\dot{q}}_2\right)\right],$

3

$m_{a3}{\ddot{z}}_{a3}=\left[k_{a3}\left(z_{b1}+l_3{\phi }_{b1}-z_{a3}\right)+c_3\left({\dot{z}}_{b1}+l_3{\dot{\phi }}_{b1}-{\dot{z}}_{a3}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{t3}\left(z_{a3}-q_3\right)+c_{t3}\left({\dot{z}}_{a3}-{\dot{q}}_3\right)\right],$

4

$m_{a4}{\ddot{z}}_{a4}=\left[k_{a4}\left(z_{b2}+l_5{\phi }_{b2}-z_{a4}\right)+c_4\left({\dot{z}}_{b2}+l_5{\dot{\phi }}_{b2}-{\dot{z}}_{a4}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{t4}\left(z_{a4}-q_4\right)+c_{t4}\left({\dot{z}}_{a4}-{\dot{q}}_4\right)\right],$

5

$m_{a5}{\ddot{z}}_{a5}=\left[k_{a5}\left(z_{b2}+l_4{\phi }_{b2}-z_{a5}\right)+c_5\left({\dot{z}}_{b2}+l_4{\dot{\phi }}_{b2}-{\dot{z}}_{a5}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{t5}\left(z_{a5}-q_5\right)+c_{t5}\left({\dot{z}}_{a5}-{\dot{q}}_5\right)\right],$

6

$m_{b1}{\ddot{z}}_{b1}=[k_{c1}\left(z_c-l_9{\phi }_c-l_{10}{\phi }_c-z_{b1}+l_{11}{\phi }_{b1}\right)$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+c_{c1}\left({\dot{z}}_c-l_9{\dot{\phi }}_c-l_{10}{\dot{\phi }}_c-{\dot{z}}_{b1}+l_{11}{\dot{\phi }}_{b1}\right)]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\left[k_{c2}\left(z_c+l_8{\phi }_c-z_{b1}-l_{12}{\phi }_{b1}\right)+c_{c2}\left({\dot{z}}_c+l_8{\dot{\phi }}_c-{\dot{z}}_{b1}-l_{12}{\dot{\phi }}_{b1}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\left[k_k\left(z_{b2}-l_6{\phi }_{b2}-z_{b1}-l_7{\phi }_{b1}\right)+c_k\left({\dot{z}}_{b2}-l_6{\dot{\phi }}_{b2}-{\dot{z}}_{b1}-l_7{\dot{\phi }}_{b1}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_1\left(z_{b1}-l_1{\phi }_{b1}-z_{a1}\right)+c_1\left({\dot{z}}_{b1}-l_1{\dot{\phi }}_{b1}-{\dot{z}}_{a1}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a2}\left(z_{b1}+l_2{\phi }_{b1}-z_{a2}\right)+c_2\left({\dot{z}}_{b1}+l_2{\dot{\phi }}_{b1}-{\dot{z}}_{a2}\right)\right]$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a3}\left(z_{b1}+l_3{\phi }_{b1}-z_{a3}\right)+c_3\left({\dot{z}}_{b1}+l_3{\dot{\phi }}_{b1}-{\dot{z}}_{a3}\right)\right],$

7

$\begin{array}{l}{I}_{b1}{\ddot{\phi }}_{b1}=\left[k_1\left(z_{b1}-l_1{\phi }_{b1}-z_{a1}\right)+c_1\left({\dot{z}}_{b1}-l_1{\dot{\phi }}_{b1}-{\dot{z}}_{a1}\right)\right]l_1\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+\left[k_{c2}\left(z_c+l_8{\phi }_c-z_{b1}-l_{12}{\phi }_{b1}\right)+c_{c2}\left({\dot{z}}_c+l_8{\dot{\phi }}_c-{\dot{z}}_{b1}-l_{12}{\dot{\phi }}_{b1}\right)\right]l_{12}\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a2}\left(z_{b1}+l_2{\phi }_{b1}-z_{a2}\right)+c_2\left({\dot{z}}_{b1}+l_2{\dot{\phi }}_{b1}-{\dot{z}}_{a2}\right)\right]l_2\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a3}\left(z_{b1}+l_3{\phi }_{b1}-z_{a3}\right)+c_3\left({\dot{z}}_{b1}+l_3{\dot{\phi }}_{b1}-{\dot{z}}_{a3}\right)\right]l_3\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{c1}\left(z_c-l_9{\phi }_c-l_{10}{\phi }_c-z_{b1}+l_{11}{\phi }_{b1}\right)+c_{c1}\left({\dot{z}}_c-l_9{\dot{\phi }}_c-l_{10}{\dot{\phi }}_c-{\dot{z}}_{b1}+l_{11}{\dot{\phi }}_{b1}\right)\right]l_{11}\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_k\left(z_{b2}-l_6{\phi }_{b2}-z_{b1}-l_7{\phi }_{b1}\right)+c_k\left({\dot{z}}_{b2}-l_6{\dot{\phi }}_{b2}-{\dot{z}}_{b1}-l_7{\dot{\phi }}_{b1}\right)\right]l_7,\end{array}$

8

$\begin{array}{l}{m}_{b2}{\ddot{z}}_{b2}=-\left[k_k\left(z_{b2}-l_6{\phi }_{b2}-z_{b1}-l_7{\phi }_{b1}\right)+c_k\left({\dot{z}}_{b2}-l_6{\dot{\phi }}_{b2}-{\dot{z}}_{b1}-l_7{\dot{\phi }}_{b1}\right)\right]\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a4}\left(z_{b2}+l_5{\phi }_{b2}-z_{a4}\right)+c_4\left({\dot{z}}_{b2}+l_5{\dot{\phi }}_{b2}-{\dot{z}}_{a4}\right)\right]\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a5}\left(z_{b2}+l_4{\phi }_{b2}-z_{a5}\right)+c_5\left({\dot{z}}_{b2}+l_4{\dot{\phi }}_{b2}-{\dot{z}}_{a5}\right)\right],\end{array}$

9

$\begin{array}{l}{I}_{b2}{\ddot{\phi }}_{b2}=\left[k_k\left(z_{b2}-l_6{\phi }_{b2}-z_{b1}-l_7{\phi }_{b1}\right)+c_k\left({\dot{z}}_{b2}-l_6{\dot{\phi }}_{b2}-{\dot{z}}_{b1}-l_7{\dot{\phi }}_{b1}\right)\right]l_7\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a4}\left(z_{b2}+l_5{\phi }_{b2}-z_{a4}\right)+c_4\left({\dot{z}}_{b2}+l_5{\dot{\phi }}_{b2}-{\dot{z}}_{a4}\right)\right]l_5\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{a5}\left(z_{b2}+l_4{\phi }_{b2}-z_{a5}\right)+c_5\left({\dot{z}}_{b2}+l_4{\dot{\phi }}_{b2}-{\dot{z}}_{a5}\right)\right]l_4,\end{array}$

10

$\begin{array}{l}{m}_c{\ddot{z}}_c=\left[k_s\left(z_c-l_9{\phi }_c-z_s\right)+c_s\left({\dot{z}}_c-l_9{\dot{\phi }}_c-{\dot{z}}_s\right)\right]\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{c1}\left(z_c-l_9{\phi }_c-l_{10}{\phi }_c-z_{b1}+l_{11}{\phi }_{b1}\right)+c_{c1}\left({\dot{z}}_c-l_9{\dot{\phi }}_c-l_{10}{\dot{\phi }}_c-{\dot{z}}_{b1}+l_{11}{\dot{\phi }}_{b1}\right)\right]\\ \mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{c2}\left(z_c+l_8{\phi }_c-z_{b1}-l_{12}{\phi }_{b1}\right)+c_{c2}\left({\dot{z}}_c+l_8{\dot{\phi }}_c-{\dot{z}}_{b1}-l_{12}{\dot{\phi }}_{b1}\right)\right],\end{array}$

11

$I_c\ddot{\phi }=[k_{c1}\left(z_c-l_9{\phi }_c-l_{10}{\phi }_c-z_{b1}+l_{11}{\phi }_{b1}\right)$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}+c_{c1}\left({\dot{z}}_c-l_9{\dot{\phi }}_c-l_{10}{\dot{\phi }}_c-{\dot{z}}_{b1}+l_{11}{\dot{\phi }}_{b1}\right)]\left(l_9+l_{10}\right)$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_{c2}\left(z_c+l_8{\phi }_c-z_{b1}-l_{12}{\phi }_{b1}\right)+c_{c2}\left({\dot{z}}_c+l_8{\dot{\phi }}_c-{\dot{z}}_{b1}-l_{12}{\dot{\phi }}_{b1}\right)\right]l_8$
$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}-\left[k_s\left(z_c-l_9{\phi }_c-z_s\right)+c_s\left({\dot{z}}_c-l_9{\dot{\phi }}_c-{\dot{z}}_s\right)\right]l_9,$

12

$m_s{\ddot{z}}_s=-\left[k_s\left(z_c-l_9{\phi }_c-z_s\right)+c_s\left({\dot{z}}_c-l_9{\dot{\phi }}_c-{\dot{z}}_s\right)\right].$

2.2. Suspension dynamic model

Air springs for the rear axles of tractor and trailer: Schematic of an air spring is shown in Fig. 2(a). The air spring dynamic model for the air spring suspension systems is selected in this paper, as shown in Fig. 2(b). The dynamic model of the leaf spring suspension system is shown in Fig. 2(c).

In Fig. 2, $p_e$ is the absolute pressure in the air chamber (Pa), $p_a$ is the atmospheric pressure (Pa), and $A_e$ is the effective area (m²), $V_e$ is the effective volume; $z_a$ and $z_b$ are the displacements of axle and vehicle body, $k_a$ and k are stiffness coefficients of air and leaf spring suspensions, $c$ is damping coefficients.

Based on the references [3, 4], the equivalent stiffness can be given as follows:

13

$k_a=n\left(p_g+p_a\right)\frac{A_e^2}{V_e}+p_g\frac{d{A}_e}{dz}=n\left[p_a+\left(p_0+p_a\right){\left(\frac{V_0}{V_e}\right)}^n-p_a\right]\frac{A_e^2}{V_e}+\frac{d{A}_e}{dz}\left[\left(p_0+p_a\right){\left(\frac{V_0}{V_e}\right)}^n-p_a\right].$

The air-spring suspension vertical force (see Fig. 2(b)) is defined as:

14

$F=k_a\left(z_b-z_a\right)+c\left({\dot{z}}_b-{\dot{z}}_a\right).$

The leaf-spring suspension vertical dynamic force (see Fig. 2(c)) is defined as:

15

$F=k\left(z_b-z_a\right)-c\left({\dot{z}}_b-{\dot{z}}_a\right).$

Fig. 2Suspension dynamic model

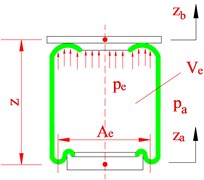
a) Schematic of an air spring

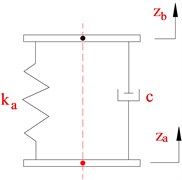
b) Air spring suspension

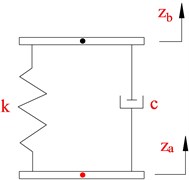
c) Leaf spring suspension

3. Optimization via genetic algorithm

There are many optimal algorithms used to find out the optimal parameters of the suspension to improve vehicle ride comfort as well as reduce the dynamic wheel load acting on road surface such as Genetic algorithm (GA) [6, 7, 9], NSGA-II, SPEA2, PESA-II [8], and MUGA [10]. Genetic algorithm (GA) is used to search the optimal design parameters for air suspension systems. In the genetic algorithm process is as follows[18]: [Start] Generate random population of $N$ individuals, i.e. suitable solutions for the problem; [Fitness] Evaluate the fitness of each individual in the population; [New population] Create a new population by repeating following steps until the New population is complete: Selection, Crossover, Mutation and Accepting; [Replace] Use new generated population for a further run of the algorithm; [Test] If the end condition is satisfied, stop, and return the best solution in current population; and [Loop] Go to the second step for fitness evaluation. Dynamic load coefficient (DLC) defined as a ratio of the root mean square (r.m.s) of the vertical dynamic wheel force over static wheel load [1, 3, 11, 12, 16] as follows:

where, $F_{T,rms}$ is the r.m.s of the vertical dynamic and $F_S$ is the static wheel force.

To minimize negative impacts of the dynamic wheel forces on road surfaces, the dynamic wheel forces the variance of the dynamic load should be minimized:

Case 1: Optimal design of geometrical parameters of air spring suspension systems:

where: $F\left(X\right)$ are functions of the r.m.s of the vertical dynamic wheel forces at 1st, 2nd, 3rd, 4th, and 5th axles; $w_n$ ($n=$1-5) are the weighting coefficients, respectively $\sum _{n=1}^5{w}_n=1$ ($w_1=$0.2, $w_2=$0.2, $w_3=$0.2, $w_4=$0.2, and $w_5=$0.2); $X$ is the geometric design parameter vector of the air spring suspension systems; $∆z_j$ are the relative vertical displacement between the axles and the semi-vehicle bodies ($∆z_{jmax}=$0.127 m [15]). $k_j^{low}$ and $k_j^{up}$are the respective lower and upper bounds for each stiffness coefficients of the air spring suspension systems.

Case 2: Optimal design of parameters of air suspension systems:

where, $k_j^{low}$, $c_j^{low}$ and $k_j^{up}$, $c_j^{up}$ are the respective lower and upper bounds for each stiffness and damping coefficients of the air suspension systems.

Fig. 3Road roughness random excitation according to the standard ISO 8068

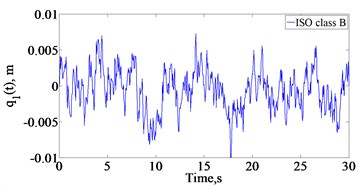
a) ISO 8068 class B

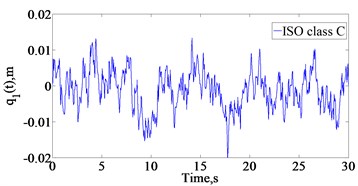
b) ISO 8068 class C

4. Conclusions

A half-vehicle dynamic model of a semi-trailer truck is established for searching the optimal design parameters of vehicle air suspensions using genetic algorithm (GA). The objective functions and boundary conditions are established in two optimal conditions: Optimal design of geometrical parameters of air spring suspension systems and optimal design of parameters of air suspension systems. The results of Part 1 in this paper provide the theoretical basis for simulation, optimization and discussion in Part 2 as the results and discussion.