Identification of loose particles using deep learning convolutional network

1. Introduction

The existence of loose particles is one of the main threats to the reliability of aerospace components, which can lead to fatal accidents. For example, a small piece of iron sheet can move to bared wires and cause short circuits. Loose particles can be brought in while producing the components and it’s hard to clear them out absolutely.

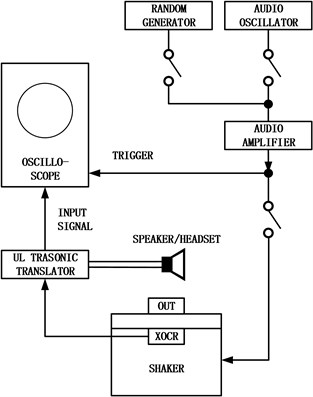
Detecting the loose particles before the components are put into use is one way to improve. Particle impact noise detection (PIND) test is a major method for detecting the presence of loose particles left inside components. Following MIL-STD-202G standard [1], the structure of PIND test is as shown in Fig. 1. Its process can be described as follows:

1) Put the component to be tested on the shaker or turntable, and attach the acoustic sensor on it.

2) The shaker produces impact and vibration, which makes loose particles inside the component free and impact with the component.

3) The impact produces acoustic signal, which is collected by the acoustic sensor. The sensor can converts the acousitc signal to electrical signal, and then output it to oscilloscope and speaker.

4) The oscilloscope can show visible waveform and the speaker can provide audible sound. The operator can use this information to determine the presence and classification of loose particles.

Besides detecting the presence of loose particles, identifying the material is also necessary. It can help find the source of loose particles and can be helpful for reducing their generation. Material identification is actually a classification problem. Traditional methods usually use machine learning to solve the problem, the usual process is extracting features from acoustic signals firstly and training classifiers then. Shujuan Wang [2] proposed a LVQ (Learning Vector Quantization)-based method which uses energy distribution vectors in wavelet domain. Long Zhang [3] compared the wavelet Fisher discriminant with AR model and LVQ neural networks and proves that the wavelet Fisher discriminant is better than others. JinBao Chen [4] uses MFCC (Mel Frequency Cepstrum Coefficient) feature to train HMM (Hidden Markov Model), achieving 91 % accuracy on 4 types of material. Meng [5] combines MFCC with other features in time and frequency domain to train SVM (Support Vector Machine) model, achieving 98 % on 3 types of material. For these methods, the performance of identification is determined by whether the features can represent information of material completely and whether the classifier can map features to classes accurately. However, the hand-craft features may be hard to characterize the material information of original signals accurately, especially for complex signals with noisy signals.

Fig. 1The structure of PIND test

In order to overcome the disadvantages of hand-craft features, we need an end-to-end algorithm which can gives the identification result directly, which means both features extraction and classification are finished by it. Recent work on speech recognition has shown good performance [6, 7]. Cummins N’s work [6] on speech emotion recognition has shown that using pre-trained CNN (convolutional neural network) to extract features from spectrograms is robust for noisy signals. Li P. [7] proposed an attention pooling based CNN which also receives a spectrogram as input, having shown excellent performance. As deep learning has not been applied on the problem of loose particles’ material identification, motivated by these works, a method using spectrogram and CNN is proposed. In this way, extracting features manually can be avoided. Instead, the network searches appropriate features from the spectrogram automatically. Experiments prove that deep learning method outperforms existing methods.

2. Method

2.2. Identification based on CNN

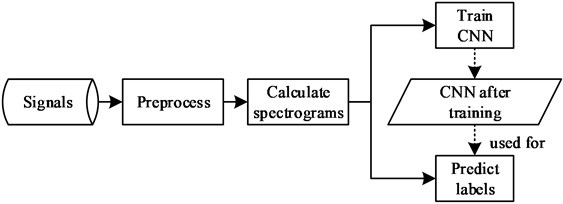
The process of material identification using deep learning includes follows: 1) Preprocess original signals to reduce noises. 2) Calculate spectrograms of denoised signals. 3) Input spectrograms with their material labels to an end-to-end CNN to train the model. 4) Use the trained model to predict test signals’ material types. It can be shown as Fig. 2.

Fig. 2Process of proposed material identification method

2.2.1. Spectrograms calculation

Before calculating spectrograms, DB4 wavelet denoising is applied on signals as preprocessing. Related work in paper [8] has proved its effectiveness. As a CNN receives images as input, spectrograms are firstly calculated.

Firstly, the signal is divided into several frames with the same length, and then a sequence of hamming windows are applied to these frames. Hamming window can be calculated as Eq. (1):

1

$W\left(l\right)=0.54-0.46\mathrm{c}\mathrm{o}\mathrm{s}\frac{2\pi l}{L-1},\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}0\le l\le L-1,$

where $L$ refers to the length of windows and should be same with frame length. Dot the signal by window to acquire the output.

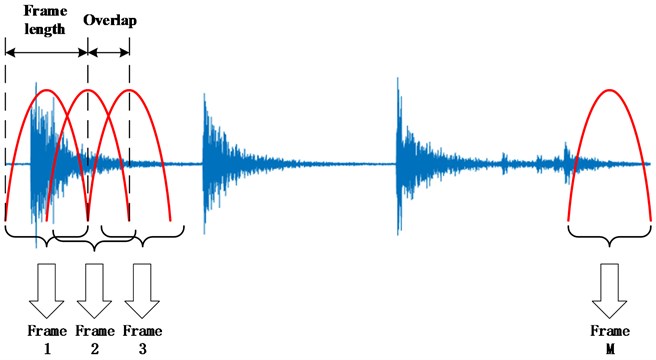
To avoid information missing at both ends of hamming window, there exists overlap between neighboring frames. Usually overlap is set to 1/3-1/2 of frame length and here we use half (0.5 ms). The process of applying windows is shown in Fig. 3.

Fig. 3Divide frames and apply hamming windows

For each frame ${\mathbf{x}}_i$ with length of $N$, we calculate the DFT (discrete Fourier transform) result as Eq. (2):

2

${\mathbf{X}}_i\left(k\right)=\sum _{n=0}^{N-1}{\mathbf{x}}_i\left(n\right)e^{-j\frac{2\pi }{N}kn}，k=\mathrm{0,1},2,...,N-1.$

Assuming that the number of frames in one signal is $M$, then we concate all the DFT results (each is a $N\times 1$ vector) and get a $M\times N$ matrix as Eq. (3):

3

$\mathbf{S}=\left({\mathbf{X}}_1,{\mathbf{X}}_2,\cdots ,{\mathbf{X}}_M\right).$

In ways similar to pseudo-color processing, the matrix can be mapped to an colored image. Thus, a spectrogram is calculated.

2.2.2. Spectrograms of loose particle signals

An example of loose particle signal with its spectrogram is shown as Fig. 4. As is shown in Fig. 4(b), the pulse signals around 0-20 ms, 45-60 ms, 65-80 ms, 85-95 ms have common features that the power around 50 kHz is especially high, and their shapes are also similar.

Fig. 4An example of loose particle signal with its spectrogram

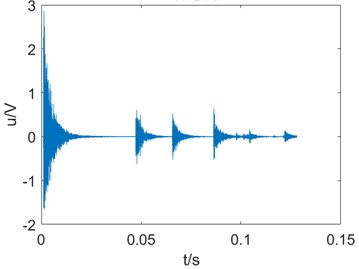
a) Signal

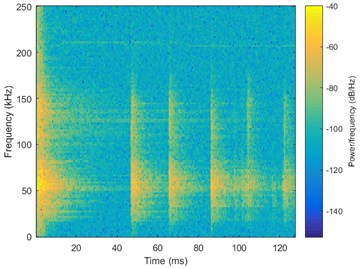
b) Spectrogram

Fig. 5 shows 2 spectrograms of different material’s loose particle signals. Epoxy’s frequency mainly focus on 50 kHz, while wire’s frequency has a higher range. On the one hand, there exists difference among spectrogram of different material’s loose particle signals. On the other hand, pulses in the same spectrogram are similar in peak position and envelope. So spectrograms are able to represent the information of material, and using spectrograms as the input of CNN is a available way to achieve automatic identification.

Fig. 5Spectrograms of different material’s PIND signals

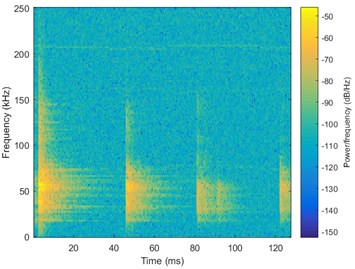
a) Epoxy

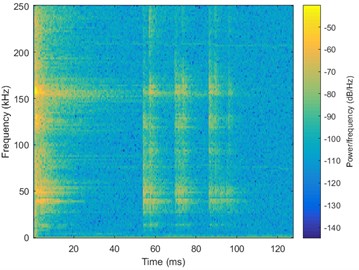
b) Wire

2.2.3. CNN architecture

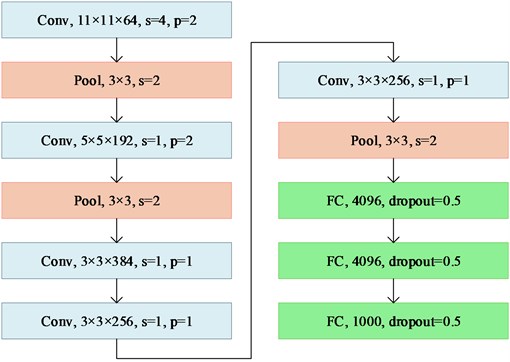
Based on AlexNet [9], a similar CNN architecture is used for classifying the spectrograms. The architecture is shown as Fig. 6. For convolution layer, 11×11×64 denotes height × width × channel of kernels. For pooling layer, 3×3 denotes height × width of kernels. Stride and padding size is denoted by s and p (where $p=$ 0 is omitted). Number in fully connected layer shows the number of nodes, and dropout percentage is also given. Besides, in order to accelerate the training process, a pre-trained model trained on Image Net database is used. Though there are 1000 class in this model, it can still be applied on 5-class problem in later experiments.

Fig. 6Network architecture

3. Experiments

For experiments, a dataset of loose particle signals are collected, including 4794 sample signals. There are 5 different types of loose particles, including tin, epoxy, tinsel, aluminum and wire. Considering mass of loose particles are usually not stable, loose particles range from 0.1 mg-4 mg are used. The dataset is divided into 2 part, 1/4 is randomly chosen for testing and others are for training. For spectrograms calculation, frame length is 1 ms and DFT length is 256.

4. Conclusions

Automatic material identification of loose particles has vital research value for improving the reliability and stability of components. Related researches before mostly used hand-craft and machine learning methods. As deep learning and spectrograms are widely used in speech recognition domain, this paper proposes to apply CNN with spectrograms on the loose particles’ material identification task. Experiments prove that the proposed method achieves higher accuracy and it is useful in practical production. The network structure used in this paper still need to be improved, and learning features from the signal directly is also an important trend in future research.