On using escort distributions in digital image analysis

2.1. Rényi spectrum

Consider a set $M\subset R^n$, and a partition on $N\left(\epsilon \right)$ boxes with box size $\epsilon$. Define a probability measure ${p\left(\epsilon \right)=\{p}_i\left(\epsilon \right)\}$, $i=1,\dots ,N\left(\epsilon \right)$, $\sum _{i=1}^{N\left(\epsilon \right)}{p}_i\left(\epsilon \right)=1.$

Consider also the generalized statistical sum (sum of moments of measure):

where $q\in R.$

For $q\in R^{+}$ introduce the function:

which specifies a class of Rényi entropies. When $q=1$ we have Shannon’s entropy:

Generalized Rényi dimensions (or Rényi spectrum) may be defined as:

But it is more common to assume that $q\in R$ and define Rényi dimensions by using Eq. (1):

It is easy to check that $D_q$ is a nonincreasing function of $q$.

In multifractal techniques, it is assumed that for a box of size $\epsilon$$p_i\left(\epsilon \right)$ satisfies the relation:

It is also assumed that:

where $\tau \left(q\right)$ is $C^1$ function.

Here and throughout the symbol $~$ indicates the asymptotic relation, namely Eq. (5) and Eq. (6) should read:

Taking into account the assumptions made we may write Eq. (4) in the form:

Note that as a rule we choose a partition of the set considered so that $p_i\left(\epsilon \right)\le {\epsilon }^{{\alpha }_i}$, but some authors consider the partition with boxes of size $\epsilon$ such that $p_i\left(\epsilon \right)\ge {\epsilon }^{{\alpha }_i}$ and assume that $S(q,\epsilon )~{\epsilon }^{-\tau \left(q\right)}$ [9]. In this case we have:

Rényi dimensions for $q=$ 0, 1, 2 are respectively capacity, information and correlation dimensions. In this work we use information dimension:

Rényi spectrum $\left\{D_q\right\}$ may be successfully applied as a classifying sign in image analysis. In [10] generalized dimensions were used to define the degree of destruction of metal; in [11] the authors analyzed and classified images of petroglyphs of Karelia. The papers [12, 13] are devoted to the application of Rényi spectra to the analysis of images of biomedical preparations.

2.2. Direct multifractal transformation and escort distribution

Consider an initial measure $\left\{p_i\right(\epsilon \left)\right\}$ and the measure $\left\{{\mu }_i\left(q,\epsilon \right)\right\}$ obtained by the following transformation:

This formula defines a sequence of renormalization of initial distribution, and the transformation is called direct multifractal transformation. If $p_i\left(\epsilon \right)=const$ (and hence $=1/N\left(\epsilon \right))$ then ${\mu }_i\left(q,\epsilon \right)=p_i\left(\epsilon \right)$ for any $q$. Because of this, it is natural to interpret the transformation as a method to reveal a degree of nonuniformity of the initial measure. The transformations form a group: there are unity and inverse elements for $q\ne 0,$ and for $q=0$ the uniform distribution is the fixed point of the transformation. With respect to the transformation the set of all probability measures is divided into nonintersecting equivalence classes. It means that when changing $\epsilon$we come to different initial measures $p_i\left(\epsilon \right)$, and different sequences of measures given by Eq. (9). The set of generated measures gives a multifractal description of an image (object).

It is interesting to note the connection of the sequence Eq. (9) with a class of optimization problems (conditional extremum task). Let $p=\left\{p_i\right\}$, $i=1,\dots ,N$, $\sum _{i=1}^N{p}_i=1$ be a probability measure defined on a partition with a given box size. Find the distribution $\left\{{\mu }_i\right\}$ maximizing Shannon's entropy $-{\sum }_{i=1}^N{\mu }_i\ln {\mu }_i$ subject to the conditions that:

The solution of the problem is so called escort distribution:

where $\beta$ – the Lagrange multiplier. It is defined from the conditions Eq. (9a). The distribution Eq. (10) is a particular case of Eq. (9), where the Lagrange multiplier is considered as a parameter.

Thus distribution Eq. (9) may be interpreted as a parametrized set of solutions for a sequence of optimization problems of the given class. In other words, for any initial probability distribution $p=\left\{p_i\right\}$ there is the distribution of the form Eq. (10) that maximizes Shannon entropy under the conditions Eq. (9a). And vice versa, there is $\beta$ such that the distribution Eq. (10) solves the optimization problem described.

2.3. From Rényi spectrum to the multifractal one. Legendre transformation

Rényi spectrum describes the changing of an initial measure by the use of its moments. Multifractal spectrum shows the distribution of the measure in accordance with singularity components ${\alpha }_i$, namely consists of fractal dimensions of subsets which are unions of boxes having close values of exponents. In literature it is also known as scaling spectrum.

A natural method accepted in multifractal formalism to connect Rényi spectrum (defined by parameter$q)$ and multifractal spectra (defined by scaling exponents) is to assume that the number of boxes with exponent $\alpha$ is distributed with a probability density.

Denote by $n\left(\alpha \right)$ the number of boxes with exponents ${\alpha }_i$, such that ${\alpha }_i\in \left[\alpha ,\alpha +d\alpha \right].$ Then the probability that ${\alpha }_i$ belongs to this interval is ${\int }_{\alpha }^{\alpha +d\alpha }n\left(z\right)dz\approx n\left(\alpha \right)d\alpha$. It is also assumed that $n\left(\alpha \right)~{\epsilon }^{-f\left(\alpha \right)}$, where $f\left(\alpha \right)$ is a differentiable function. It is the fractal dimension of the set of boxes with exponent $\alpha$. In such a manner we model a distribution of the measure on nonintersecting subsets having different fractal dimensions.

In terms of the probability density generalized statistical sum may be written as:

To take all the boxes with a given exponent $\alpha$ we have to find $\alpha$ for which the integrand function has maximum. Clearly this value depends on $q$.

As $\epsilon$ is small enough the integrand is maximal when $q\alpha -f\left(\alpha \right)$ is minimal. The conditions of extremum existence is $\frac{d}{d\alpha }(q\alpha -f\left(\alpha \right){|}_{\alpha =\alpha \left(q\right)}=0\mathrm{}$, and we obtain:

The value of the integral in Eq. (11) is proportional to the value of the integrand in the extremum point $\alpha =\alpha \left(q\right)\text{,}$ and substituting this value in Eq. (11) we have $S(q,\epsilon )\approx {\epsilon }^{q\alpha \left(q\right)-f\left(\alpha \left(q\right)\right)}$. Thus, for any $q$ we find the fractal dimension of the set consisting from the boxes with exponent $\alpha =\alpha \left(q\right).$

According to Eq. (6) we obtain the relation between $\tau \left(q\right)$ and $f\left(\alpha \right)$:

Note that:

Using Eq. (7) we obtain $D_q=\frac{1}{q-1}(q\alpha \left(q\right)-f\left(\alpha \left(q\right)\right).$

The transfer from variables $\left\{q,\tau \left(q\right)\right\}$ to $\left\{\alpha ,f\left(\alpha \right)\right\}$ is given by formulas Eq. (13) and Eq. (14) and is called the Legendre transformation. Inverse transformation from $\left\{\alpha ,f\left(\alpha \right)\right\}$ to $\left\{q,\tau \left(q\right)\right\}$ is performed by using Eq. (12) and $\tau \left(q\right)=\alpha \frac{df\left(\alpha \right)}{d\alpha }-f\left(\alpha \right).$ It is useful to note that Eq. (13) leads to the calculation of $\tau \left(q\right)$ via $\alpha \left(q\right)$ and $f\left(\alpha \left(q\right)\right)$, and $D_q$.

The detailed description of the Legendre transformation is given in [15, 16].

2.4. From multifractal spectrum to Rényi

The main approach to calculation of the Rényi spectra was initially based on Eq. (4) and Eq. (7), where for finding $\tau \left(q\right)=\underset{\epsilon \to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\ln \mathrm{}S(q,\epsilon )}{\ln \epsilon }$ the approximation by linear regression method is used. It has been noted by many researchers that this way may lead to large calculation errors.

In [17] a more sophisticated method was proposed, which allows us to find $\tau \left(q\right)$ more accurately, namely by using relation Eq. (13) and special sequences $\alpha \left(q\right)$ and $f\left(\alpha \left(q\right)\right)$. The author considered escort distributions defined by Eq. (9). For these measures in view of assumptions Eq. (5) and Eq. (6) we have ${\mu }_i\left(q,\epsilon \right)~{\epsilon }^{{q\alpha }_i-\tau \left(q\right)}~{\epsilon }^{f\left({\alpha }_i\right)}$. These distributions form an ensemble of measure theoretic supports, and the support of $\mu \left(q,\epsilon \right)$ consists of boxes having singularity exponent ${q\alpha }_i-\tau \left(q\right).$ The main idea of the method is to calculate a spectrum of singularity exponents and fractal dimensions of obtained measure theoretic supports (information dimensions) as the functions of parameter $q.$ Excluding $q$ we obtain $f\left(\alpha \right)$. When dealing with such a sequence of measures the spectrum of singularity exponents seems to be a set of derivatives of $\tau \left(q\right)$ with respect to $q$, and the Legendre transformation holds. Hence, we may find the Rényi spectrum via parametrized spectra by using Eq. (4). Thus, in image analysis it may be sufficient to use only the spectra $\alpha \left(q\right)$ and $f\left(\alpha \left(q\right)\right)$. In [18] parametrized spectra were successfully applied to analyze images of biological preparations obtained by the method of crystallization with additives.

Consider a set $M$ in phase space and its partition $\left\{M_i\right\}$ on $N\left(\epsilon \right)$ boxes of size $\epsilon$. Let $\left\{p_i\right(\epsilon \left)\right\}$ – a normed measure defined on $\left\{M_i\right\}.$ Construct a sequence of measures $\mu \left(q,\epsilon \right)=\left\{{\mu }_i\left(q,\epsilon \right)\right\}$ by using direct multifractal transformation Eq. (9). Calculate averages of exponents${\alpha }_i$ over $\mu \left(q,\epsilon \right)$:

and the limit of $\alpha \left(q,\epsilon \right)$ when $\epsilon$ tends to zero:

For each measure $\mu \left(q,\epsilon \right)\mu (q,l)$ calculate the information dimensions $f\left(q\right)$ of its support:

Thus, we obtain two spectra: information dimensions of supports of the measures from a given sequence, and the set of averaged exponents calculated with respect to the measures as the functions of $q$. To calculate $f\left(q\right)$ ($\alpha \left(q\right)$ respectively) one should for every $q$ take several values of $\epsilon$, calculate points $\left(\ln \epsilon ,f\left(q,\epsilon \right)\right)$ (or $(\ln \epsilon ,\alpha (q,\epsilon \left)\right)$) and by applying the least square method obtain approximate values for $f\left(q\right)$ ($\alpha \left(q\right)).$

Now we can find the derivative of $\tau \left(q\right)$ with respect to $q$. We have:

Besides that:

This is the Legendre transformation and:

2.5. Rényi divergences

For given distributions $p=\left\{p_i\right\}$ and $v=\left\{v_i\right\}$ Rényi (or $\alpha$-) divergences for $\alpha >0$, $\alpha \ne 1$ are defined by the formula:

It is easy to check that $D_{\alpha }(p,v)$ is nonnegative and decreases as a function of $\alpha$. For $\alpha =1$ this divergence is defined as:

and called the Kullback-Leibler divergence.

For image analysis we propose to calculate Rényi divergences on the sequence of escort distributions. As mentioned above, the supports of these measures are nonintersecting subsets of a given multifractal set. When comparing images we use a vector of divergences instead of one value. The main sign of the closeness of images is the rate of the growth of the vector: for images with similar texture the vector grows more slowly than for images from different cl asses.

2.6. The estimation of the rate of the growth for the divergence vector

For given distributions $p=\left\{p_i\right\}$ and $v=\left\{v_i\right\}$ introduce the notations ${\mu }_i\left(k\right)=\frac{p_i^k}{{\sum }_{i=1}^n{p}_i^k}$ and ${\nu }_i\left(k\right)=\frac{v_i^k}{{\sum }_{i=1}^n{v}_i^k}$. Estimate the 1-divergencies between the members of corresponding sequences of measures $\mu$and $\nu ,$ constructed for initial measures $p$ and $v$:

Let:

Then:

Hence ${\sum }_i\frac{p_i^k}{{\sum }_i{p}_i^k}\ln {\sum }_i{v}_i^k/{\sum }_i{p}_i^k\le nk\ln (r/u)$ and:

For $\alpha \ne 1$:

Assume that:

Then we have:

Denote by $u_p=p_{max}/p_{min}$, $u_v=v_{max}/v_{min}$.

Then:

The obtained estimations show that the rate of the growth of the vector of divergences depends on the power of multifractal transformation $k$, parameter $\alpha$ and a characteristic of the nonuniformity of the distributions $p$ and $v$, which is estimated by $u_p$, $u_v$.

The complexity (both in time and from memory) of the implemented algorithm is $О\left(kL\right)$, where $L$ – the number of pixels in an image.

3.1. Pharmaceutical solutions with silver nanoparticles

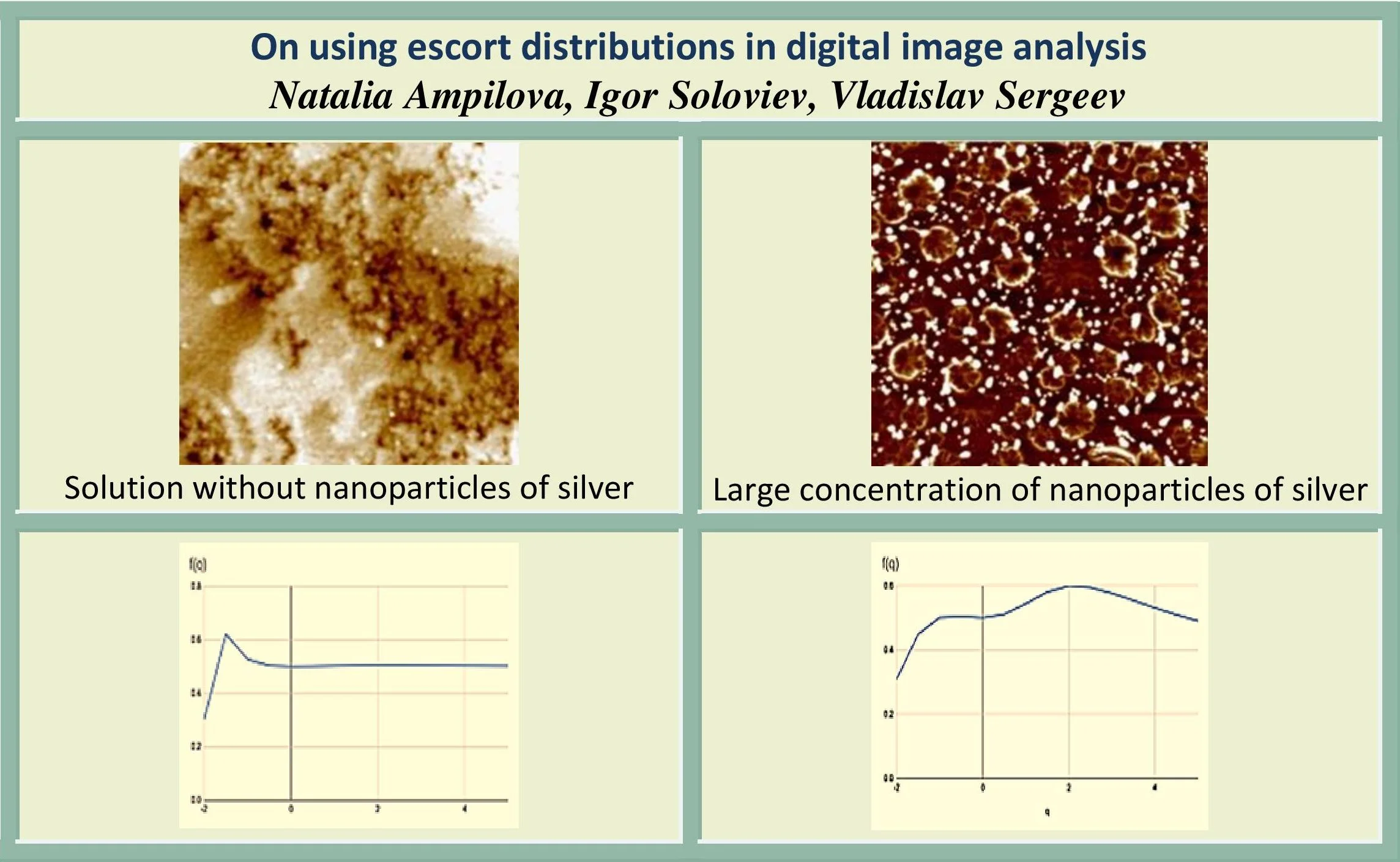
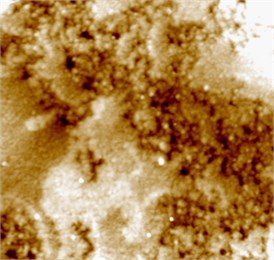
We consider images of pharmaceutical solutions in which silver nanoparticles in small and large concentrations were added. The solidified solutions without silver do not contain any organized structures. The structures appear when nanoparticles are added. All the images were obtained by using an atomic-force microscope on NTEGRA platform and have the size 658×636. The images are obtained in monochrome representation.

Fig. 1a) Solution without nanoparticles, b) small concentration of nanoparticles, c) large concentration of nanoparticles

a)

b)

c)

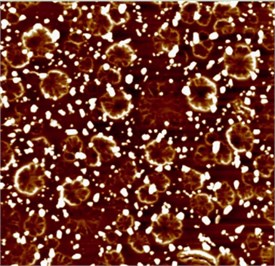
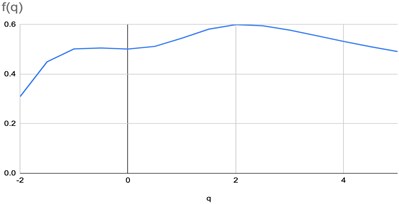
Fig. 2The graphs of parametrized spectra for the image of pharmaceutical solution without silver nanoparticles

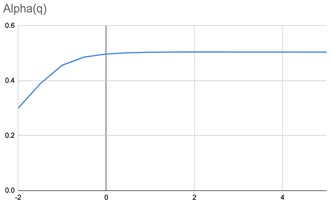
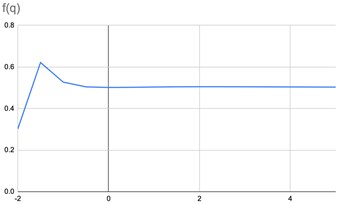
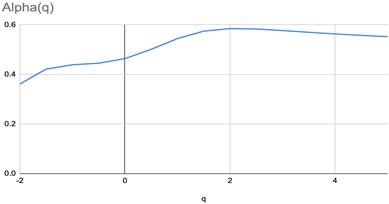
All the calculations were performed in greyscale palette, the measure of the box was taken as the normed sum of pixel intensities. The graphs of parametrized spectra for images Fig. 1(a)-(c) are shown below. The parameter $q$ changes in the interval [–2, 5] with step 0.5.

Fig. 3The graphs of parametrized spectra for the image of pharmaceutical solution with small concentration of silver nanoparticles

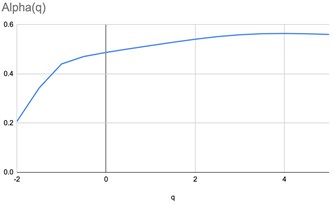
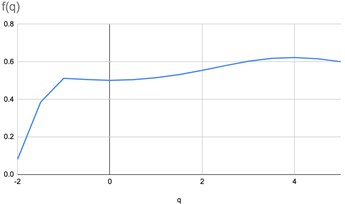
Fig. 4The graphs of parametrized spectra for the image of pharmaceutical solution with large concentration of silver nanoparticles

The results of calculations of the divergence vectors for $\alpha =$ 0.5, 1, 2 are given below. In Fig. 5 the result of comparison of Fig. 1(a) and Fig. 1(b) (zero-small) is shown. Fig. 6 demonstrates the difference in structures between Fig. 1(a) and Fig. 1(c) (zero-large).

Fig. 5Vectors of divergences obtained when comparing images Fig. 1(a) and Fig. 1(b) (zero-small)

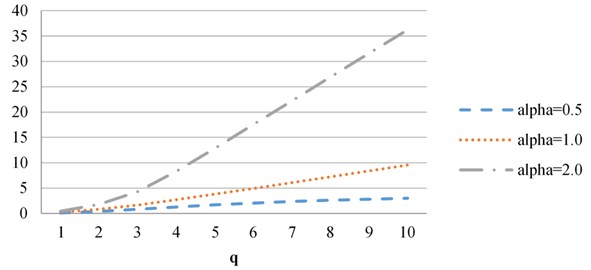
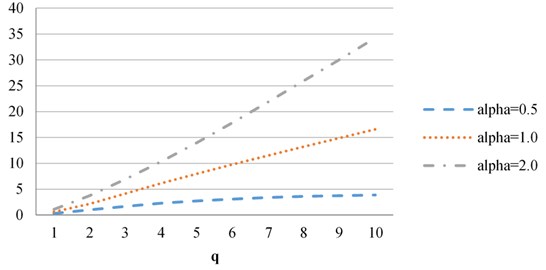
We see that the difference between images with zero and small concentration is smaller than between zero and large. Graphs of divergence vectors lend credence to the estimations on the rate of the growth of the vectors depending on $k$ and $\alpha$.

Fig. 6Vectors of divergences obtained when comparing images (a) and (c) (zero-large)

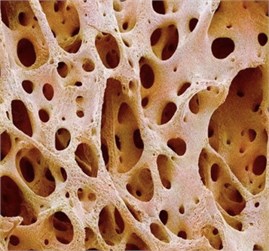
3.2. Images of bone tissue

Consider the images of healthy tissue Fig. 7(a) and bone tissue with osteoporosis Fig. 7(b). The size is 412×400. Calculations were also performed in greyscale palette; the measure of the box is the normed sum of pixel intensities. The parameter $q$ changes in the interval [–5, 5] with step 0.5.

Fig. 7a) Healthy bone, b) osteoporosis

a)

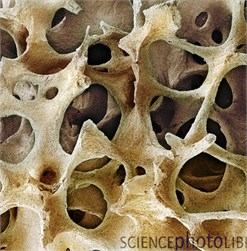
b)

Fig. 8Graphs of parametrized spectra for the image of healthy bone (а)

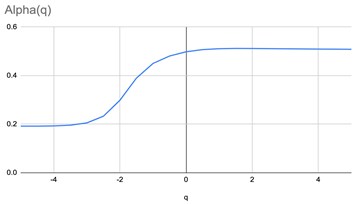
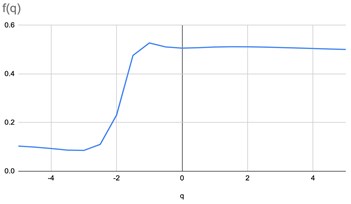
Fig. 9Graphs of parametrized spectra for the image of bone with osteoporosis (b)

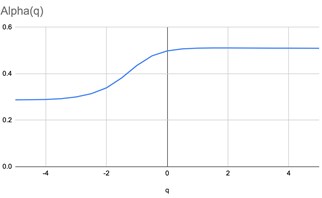
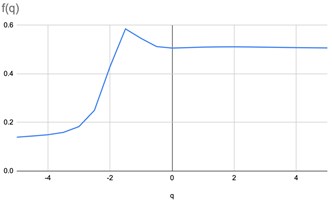
Fig. 10Vectors of Rényi divergences when comparing healthy bone and bone with osteoporosis

In this case vectors of divergences grow more slowly than in the previous example. This reflects a visual similarity of images in spite of the fact that they are in different classes. But a combination of the two methods makes it possible to distinguish between images.