Multi-objectives robust optimization based on Grey-Taguchi method for the electric vehicle frame collision

1. Introduction

Energy conservation, environmental protection, and safety is an important theme in the development of automobile technology in this century. The energy conservation and environmental protection of electric vehicles have been widely recognized by the government, automobile manufacturers, and consumers. The driving safety of electric vehicles in various situations is becoming research focuses, when the endurance mileage of electric vehicles is being gradually enhanced, with the development of power battery technology in the past few years.

Passive safety technology is still concerned by scholars and engineers, especially the crashworthiness and lightweight design of electric vehicles [1].

The contradiction between lightweight design and crashworthiness design is a typical multi-objective optimization problem. Some scholars can well solve the multi-objective optimization problem of the vehicle collision with the intelligent optimization and surrogate model technology [2]. However, it is generally known that surrogate model techniques were found difficult to deal with high-dimension and high nonlinear problems [3]. There are many design variables involve in the design of the vehicle crashworthiness and lightweight. This makes it difficult for the surrogate model technology to meet the precision requirements.

In addition, these design variables are also uncertain and the discrete parameters exist in the products. Therefore, vehicle collision design is a multi-objective robust design problem with discrete variables, and there are few reports on this kind of problem [4].

Taguchi method is a robust optimization design that implemented the signal-to-noise ratio (SNR) and orthogonal table to optimization. To complete the experimental design, parameters must be discretized. Therefore, the robust design method of Taguchi provides the possibility to solve the above problems. But the Taguchi method has its own problems. To eliminate the shortcomings of the Taguchi, the grey relation analysis (GRA) is utilized herein to convert multiple objectives to a single grey relation grade (GRG) sequence by the linear weighted sum method. In recent years, the implementation of GRA for robust design has received attention [5]. Sun et al. [3] and Xie et al. [6] further extended the Grey-Taguchi method to the multi-objective robust optimization design.

However, with the increase of the number of control variables and discrete levels, the experiment was designed so many times that it could not be done.

The purpose of this paper is to use the Grey-Taguchi robust optimization design method that found and iterated the optimal combination with the minimum experimental design table in order to solve the multi-objective robust optimization problem for an electric vehicle collision with discrete variables.

2. Problem description for the frame collision

2.1. The simulation model of the frame collision

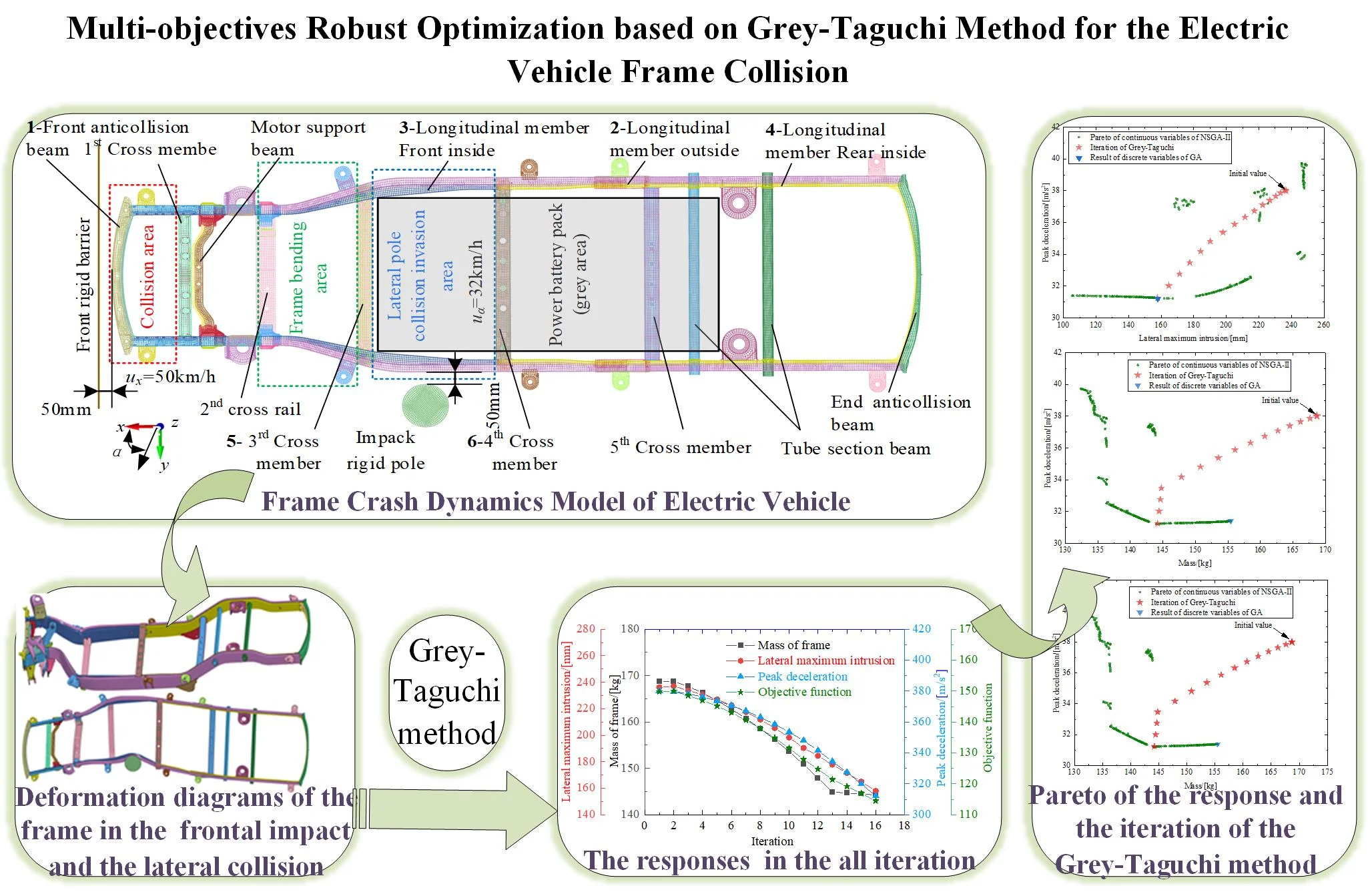
This paper studies the kick-up frame structure, which is used for electric SUV vehicles. The two sides of the frame are longitudinal members, front and end of the frame have anti-collision beams and there are 5 cross members in the middle, a motor support beam is between the first and second cross member, and two tube section beams are between the fifth cross member and the end anti-collision beams, as shown in Fig. 1. The collision area is set with the front anti-collision beam and the longitudinal member in front of the first member. The battery pack is installed between the 3rd cross member and the front tube section beam.

Fig. 1The Kick-up frame construction and part number

The collision finite element model for the frame was established by the software of HyperWorks/LS-DYNA, and the shell element size is 10 mm. There are 79,537 elements and 84,89 nodes of the frame.

For the collision of electric vehicles, we should not only consider the safety of occupants in the collision process but also consider that the power battery pack is not invaded by objects. Therefore, we simulate the two working conditions of a frontal collision and lateral collision. The rigid barrier is set at the front of the frame and the lateral pole is shown on the left side of the frame in Fig. 1, the simulation parameters are listed in Table 1.

Table 1The simulation parameters for working conditions

Working conditions	Speed / (km/h)	Direction of frame movement	Standard
Frontal collision with full overlap against a rigid barrier	50	$x$ direction	GB 11551-2014
The lateral pole collision	32	Rotates 75° in the $x$ direction	GB/T 37337-2019

3. Robust optimization procedure of Grey-Taguchi for discrete variables

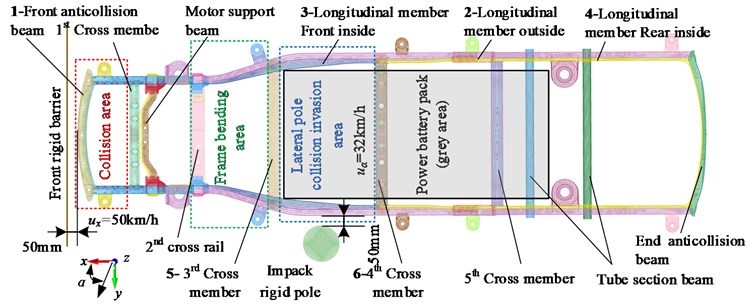
The flowchart of implementing the proposed Grey-Taguchi method is illustrated in Fig. 2. The detailed steps of the method are depicted as follows:

Step 1: Definition of the optimization problem. Set up the mathematical model of the multi-objective discrete robust optimization problem in terms of the objective functions, constraints, design variables, and noise factors.

Step 2: The procedural details of a Taguchi parameter design can be summarized as follows:

(1) Determine the control factors (the design variables such as the thickness of the members) and noise factors. In this paper, the noise factor is the elasticity modulus of the material.

(2) Construct an experimental design table, where the control factors and the noise factors that are sampled through an orthogonal design are arranged in a form of inner and outer tables, respectively. In this paper, there are only 3 levels for the control factors, the initial values or the optimal value of previous cycle assigned to the second layer. The smaller discrete values and the larger discrete values were set as the first and third levels at an interval of 0.1. The minimum orthogonal array L₂₇(3⁶) was adopted for the inner table. The noise factors have two levels: the normal and the lowest limit of the elastic modulus of the material. The noise factors were set in an external array.

(3) Run the simulation model and extract the functional responses from the simulation results.

Step 3: Choose the preference function. In this paper, we minimize all the response, so we choose the lower-the-better criterion as the preference function, as Eq. (2):

where $x_i\left(k\right)$ (the components of $\mathbf{x}$) are normalized value; $i$ is the design candidate, $i=\mathrm{1,2}$, $k=\mathrm{1,2},\cdots ,N$, $N$ are the numbers of the response function.

Fig. 2The flowchart of the proposed Grey-Taguchi method

Step 4: Calculate the GRG by the GRA method.

First, the grey relational coefficient (GRC) ${\gamma }_{0i}$ can be determined as Eq. (3):

where $x_0\left(k\right)$ is the reference sequence that is the ideal normalized for the $j$th performance characteristic. $\xi$ is the identification or distinguishing coefficient (0 $\le \xi \le$1), which is typically taken as 0.5. For our study, the value of $\xi$ was also set to be 0.5. $i=\mathrm{1,2}$ and $k=\mathrm{1,2},\cdots ,N$, $N$ is the number of quality characteristics.

Then, a weighted-sum of the GRC is implemented to calculate the grey relational grade (GRG) $\mathbf{r}=[r_1,r_2,\cdots ,r_N{]}^T$ by using Eq. (4). The essence of this step is to transform the multi-objective optimization problem into a single-objective optimization problem:

where ${\omega }_i$ is the weight coefficient. The weight of frame mass, maximum lateral intrusion, and maximum acceleration were 0.4, 0.3, and 0.3 respectively.

Step 5: Determine the optimal combination of variables by the analysis of mean (ANOM). When the grey relational grade is obtained, the ANOM is used to determine the optimal levels of design variables. Based on the GRG values, the ANOM is conducted to determine the optimal combination of variables. Regardless of the category of the preference function, a higher GRG corresponds to a better optimal result.

Step 6: Stopping Criterion. In this study, the successive procedure is terminated if the number of iterations over which the GRG of new levels is no longer improved over two iterations, or if the number of iteration ANOVAs reaches the predefined maximum; otherwise the design process returns to Step 2. In this step, the new levels from Step 5 are set to be the second levels until one of the convergence criteria is satisfied. The better variables are set to be the second levels for the next iteration until one of the convergence criteria is satisfied.

4. Results and discussions

4.1. Frame collision simulation results and test verification

The frontal collision test for the whole vehicle was tested in the safety laboratory of the National Automobile Quality Supervision and Inspection Center (Xiangyang) on May 9, 2016.

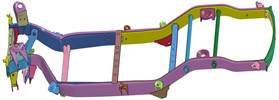
The collision deformation diagrams of the frame with the equivalent mass in the frontal collision and the lateral pole collision are shown in Fig. 3(a) and Fig. 3(b), respectively.

The deformation mode of the frame is consistent when comparison of the simulation model and the real vehicle crash test. For example, the bending deformation of the front anti-collision beams, multi-layer wrinkled deformation of the energy-absorbing box, and the bending deformation at the bending area of the kick-up frame, etc. The deformation form of the lateral pole collision is also consistent with the actual situation.

Fig. 3Deformation diagram of the frame with equivalent mass, a) the frontal impact deformation diagram; b) the lateral collision deformation diagram

a)

b)

4.2. Results of robust optimization

In this paper, the Grey-Taguchi method was used for the robust multi-optimization design of the frame crashworthiness with the discrete variables in the frame collision model.

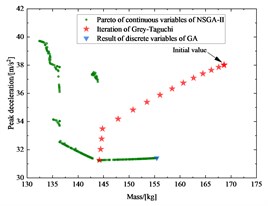
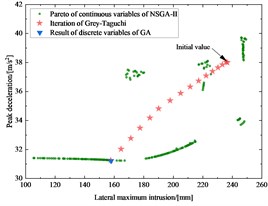
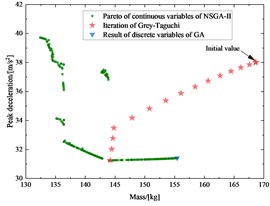
The optimization process was terminated after 16 iterations and the convergence history of the response and GRG were plotted in Fig. 4. To further justify the validity of the results, the multi-objective discrete optimization without considering the fluctuation and the multi-objective Pareto front was also performed, as shown in Fig. 5. The above multi-objective Pareto front was solved by constructing a polynomial model and using the NSGA-II algorithm.

Fig. 4The responses and GRG in the all iteration

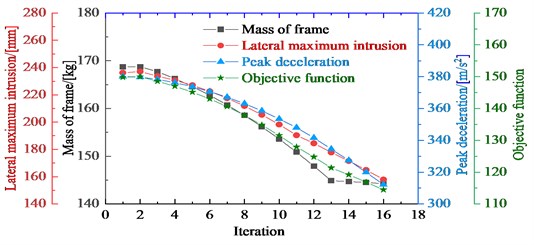
Fig. 5 shows that both the Grey-Taguchi method and the multi-objective discrete optimization without considering fluctuations can converge to the Pareto frontier, but their optimal solutions are different. The multi-objective discrete optimization has the better lateral maximum intrusion and peak deceleration, but it does not achieve a lightweight design.

The mass of frame, maximum lateral intrusion, and peak deceleration after the optimization were decreased by 14.5 %, 32.3 %, and 17.8 %, respectively with the Grey-Taguchi method. The Grey-Taguchi method achieves both lightweight design and crashworthiness. Compared with the initial design, it can be noted that the Grey-Taguchi method was not only capable of improving the performance but also enhancing the robustness of optimal designs.

More importantly, the robust optimization of the Grey-Taguchi method can be directly applied in practical applications with the simple DOE and does not require the use of the surrogate model as other robust optimization approaches do.

Fig. 5Pareto of the mass of frame, maximum lateral intrusion and peak deceleration, and the iteration of the Grey-Taguchi method

a)

b)

c)

5. Conclusions

In this paper, a robust frame crashworthiness problem with multiple objectives and discrete design variables was designed using the Grey-Taguchi method, based on validated frame frontal and side-impact dynamics models.

For the vehicle crashworthiness problem, the Grey-Taguchi method can converge to the Pareto front with several iterations. The mass of frame, maximum lateral intrusion, and peak deceleration after the optimization were decreased by 14.5 %, 32.3 %, and 17.8 %, respectively.

The Gray-Taguchi method can not only enhance the robustness of the optimization design but also improve the lightweight design performance and crashworthiness.