Analyzing the compacting energy and force distribution during the tamper-asphalt mixture interaction

2.1. The dynamics model of the tamper-asphalt mixture interaction

The paving layer of asphalt material was created based on the compacting method. under impacting of the compacting mechanisms during periodic compaction of the tamper-asphalt mixture interaction, the hot mix asphalt was then added and compacted to a fixed volume. After several compression cycles, the air and moisture in the hot mix asphalt could be completely discharged, and the density of the asphalt layer could be increased [8, 16]. Based on the dynamics model of the vibration screed system in Ref. [5], as shown in Fig. 1(a), a dynamics model describing the interaction process between the compacting mechanism and the hot mix asphalt is then established in Fig. 1(b).

Fig. 1(b), $v$ is the moving speed of the asphalt paver, $F$ is the compacting force of the compacting mechanism, $x$ is the translational displacement of the compacting mechanism after each compaction cycle, $h$ is the stroke of the vibration tamper, $c$ is the compensation of the thickness of the hot mix asphalt, and $H$ is the thickness of the compressed asphalt layer.

As described in Fig. 1, the compaction process of the hot mix asphalt is divided into two stages including (1) the compacting mechanism falls from the top position of $a$ down to the lowest position of $b$ with the stroke of the vibration tamper $h$ to compact the hot mix asphalt (first compacting time), then, (2) the compacting mechanism moves from the lowest position of $b$ up to the top position of $a$ and creases a gap between the compacting mechanism and the hot mix asphalt. Under the impact of the vibration screed and the gravity of the hot mix asphalt, the hot mix asphalt in the vibration screed system is then added in the gap below the compacting mechanism, the compacting mechanism continues to fall back down to compress the added hot mix asphalt (second compacting time) to increase density and compactness of the asphalt pavement.

Fig. 1The dynamic model of the vibration screed system and tamper-asphalt interaction

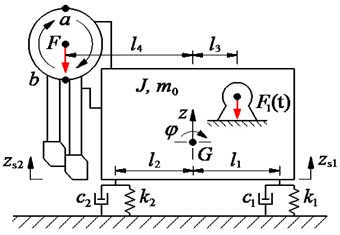
a) Vibration screed system model

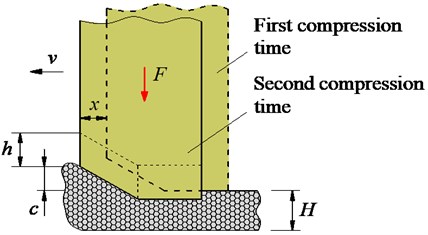
b) Tamper-asphalt mixture interaction model

Fig. 2Structure and model of the tamper-asphalt mixture interaction

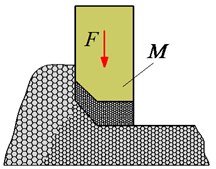
a) Practical compaction structure

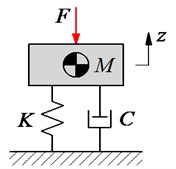
b) Equivalent compaction model

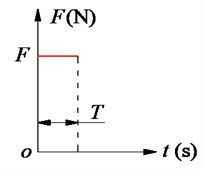
c) Compaction impulse

Due to the final density of the compacted hot mix asphalt being affected by the gradation of the asphalt material and its internal friction coefficient, therefore, the density of the asphalt mixture after compaction ${\rho }_a$ is indicated by [16, 17]:

where $\rho$ is the density of the hot mix asphalt, $\alpha$ is the loss coefficient of compactness.

Additionally, during the paving process of the asphalt paver, the traveling speed of the paver is constant while the motion of the compacting mechanism is cyclic in the vertical direction. Thus, the compacting process of the asphalt pavement is actually a combination of horizontal and vertical movements, $x$ and $z$. Therefore, the compacting force of the paver-asphalt mixture interaction and the paving quality are affected by both the traveling speed of the pave and the excitation frequency of the compacting mechanism. To elucidate the compacting energy and force distribution of the tamper mechanism on the hot mix asphalt during the tamper-asphalt mixture interaction in Fig. 2(a), a vibration model of the tamper-asphalt mixture interaction is then established Fig. 2(b). Based on the working principle of the compacting mechanism, the impacting force of the compacting mechanism on the asphalt pavement received by a rectangular pulse, as described in Fig. 2(c) [12-13, 18], is used as the excitation force to calculate the compacting force impulse of the tamper-asphalt mixture interaction. Fig. 2, $M$ is the mass of the tamper-asphalt mixture interaction determined the asphalt mixture after compaction ${\rho }_a$, parameters of $c$, $h$, and $H$, and mass of the compacting mechanisms. $K$ and $C$ are the stiffness and damping coefficients. $F$ is the excitation force of the compacting mechanism described by a rectangular pulse with unit pulse $F$ (N) and excitation time $T$ (s).

Based on the dynamic model in Fig. 2(b) and application of Newton’s second law, the dynamic differential equation of the tamper-asphalt mixture interaction is given by:

Due to the vibration excitation force $F$ of the system being a constant in excitation time $T$ (s), therefore, the solution of Eq. (2) is obtained as follows [19]:

where ${\omega }_n=\sqrt{K/M}$ is the natural frequency of the system, ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$is the damping natural frequency, and $\zeta =C/2M{\omega }_n$ is the damping ratio of the asphalt material.

At the initial time $z_0=$ 0 before the unit pulse is applied, the state of the tamper-asphalt mixture interaction is a static state. According to the momentum theorem, the momentum $F$ is determined by $F=1=M{\dot{z}}_0$. Therefore, the unit impulse response of the asphalt layer is:

2.2. Numerical simulation results

Based on the actual structure of the vibration screed system and the dynamic parameter of the tamper-asphalt mixture interaction listed in Table 1 [17], the natural frequency of the system, the damping ratio of the asphalt material, and the damping natural frequency in Eq. (3) are determined by:

Thus, the unit impulse response of $F/M{\omega }_d$ calculated in Eq. (4) is simulated and plotted in Fig. (3). Observing the result in Fig. (3), we can see that the unit impulse response of the asphalt material in the tamper-asphalt mixture interaction condition is an attenuation signal with a decay cycle of $T=1/f=2\pi /{\omega }_d=$ 2×3.14/29.5 ≈ 0.2 (s). Due to the vibration frequency of the compacting mechanism could being changed from 0 to 22 Hz [5-6], thus, the minimum/ maximum vibration time of a cycle of the compacting mechanism is $T_{min}=1/f_{max}=$ 1/22 ≈ 0.045 (s) and its $T_{max}=$ ∞. Because the energy ($E=(F{e}^{-\zeta {\omega }_{n}t}/M{\omega }_d{)}^2$) of the tamper-asphalt mixture interaction in one decay cycle is strongly reduced by 91.1 %, as shown in Fig. 3. Therefore, the compacting mechanism needs to ensure that it retains the previous vibration energy before the next vibration pulse occurs. To satisfy this requirement, the maximum vibration time of a cycle of the compacting mechanism $T_{max}$ should be smaller than the decay cycle $T=$ 0.2 (s) of the tamper-asphalt mixture interaction in Fig. 3, which means the vibration frequency of the compacting mechanism must be greater than 5 Hz ($f\ge 1/T=$ 1/0.2 = 5 Hz).

Additionally, the compacting energy of a single vibration cycle is quickly reduced up to 91.1 %, thus, it is necessary to perform multiple vibrations of the compacting mechanism on the same compaction cycle of the tamper-asphalt mixture interaction. With the width $d$, moving speed $v$, and frequency $f_c$ of multiple vibrations of the compacting force $F$ of the compacting mechanism at the same position, the number of vibrations of the compacting mechanism at the same position is defined as follows:

where the result of $N$ is 1, 2, 3, 4, 5, ..., or $n$, and $N$ depends on the ratio of $f_c/v$.

Fig. 3The excitation impulse of a single shock

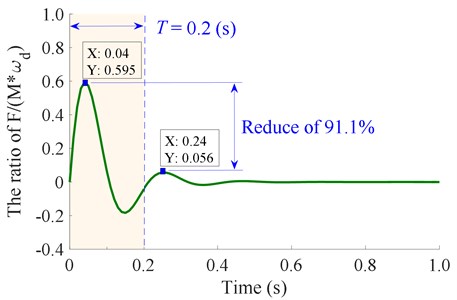
Therefore, the compacting force $F$ of the compacting mechanism at the same position should be added by multiple vibrations $f_c=Nv/d\text{,}$ and the equation of $F$ is described by $F=F_0\mathrm{s}\mathrm{i}\mathrm{n}2\pi f_{c}t$ [5]. Thereby, Eq. (4) is rewritten by:

With the $d$ is constant, the ratio of $f_c/v$ should be chosen to satisfy the condition of $N=$ 1, 2, 3, 4, 5, ..., $n$ to ensure the paving quality (because frequency and speed affect the paving quality) and retain the previous vibration energy before the next vibration pulse occurs. Based on the working parameters of the asphalt paver listed in Table 1, the maximum value of $N$ is determined by $N_{max}=d\times f_{max}/v=$ 25×10^-3×22/0.1 = 5.5, therefore, $N=$ 1, 2, 3, 4, 5 is chosen to simulate and evaluate the compacting performance and vibration energy of the compacting mechanism during the tamper-asphalt mixture interaction under the different frequencies of the compacting mechanism 5, 10, 14, 18, 22, and 26 Hz. The simulation results are shown in Fig. 4.

Observing the results in Fig. 4(a) and 4(b), we can see that when the vibration frequency $f_c$ is from 5 to 10 Hz under different vibration times of $N=$ 1, 2, 3, 4, or 5, the remaining energy in the time of 0 to 0.2 (s) of a vibration cycle is too small. This is the reason that the achieved compression efficiency of the asphalt paver in Refs. [5, 6] is very low. When the vibration frequency $f_c$ is from 14 to 18 Hz under different vibration times of $N=$ 1, 2, 3, 4, or 5, the results in Fig. 4(c) and 4(d) show that the remaining energy in the time of 0 to 0.2 (s) of a vibration cycle is significantly increased, especially at $N=$ 4 and 5. This means that the density of the compacted hot mix asphalt is increased, thus, the compaction performance of the asphalt pavement is improved. Similarly, with the vibration frequency $f_c$ from 22 to 26 Hz and under different vibration times of $N$, the results in Fig. 4(e) and 4(f) indicate that the compacting energy of the compacting mechanism is increased while its remaining energy at 0.2 (s) in a vibration cycle before the next vibration pulse occurs is quite high, particularly at $N=$ 5. Thus, the asphalt density and compression efficiency of the asphalt paver are remarkably improved under these vibration frequencies. These simulation results are similar to the experimental results of Ref. [17]. However, the existing researches have not clearly explained the compaction energy and compaction characteristic in the tamper-asphalt mixture interaction.

Fig. 4The stimulating impulse response of the tamper-asphalt mixture interaction under the different excitations of the compacting mechanism

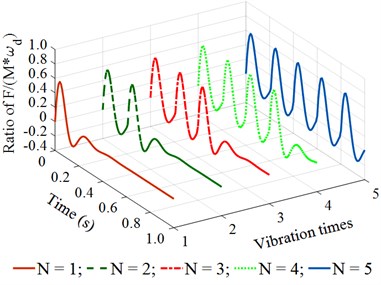
a) At an excitation frequency of 5 Hz

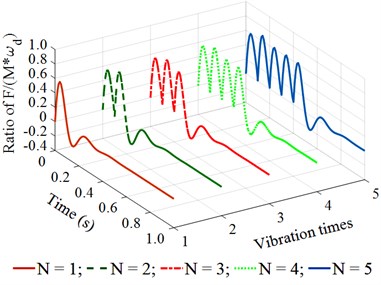
b) At an excitation frequency of 10 Hz

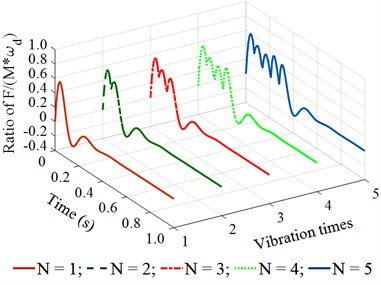
c) At an excitation frequency of 14 Hz

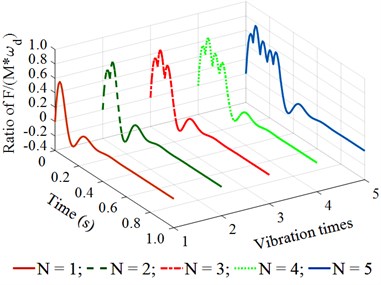
d) At an excitation frequency of 18 Hz

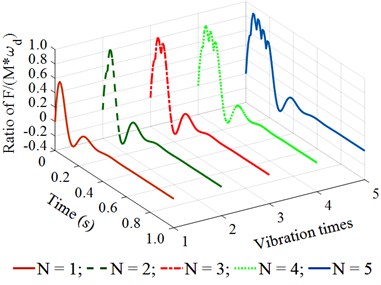
e) At an excitation frequency of 22 Hz

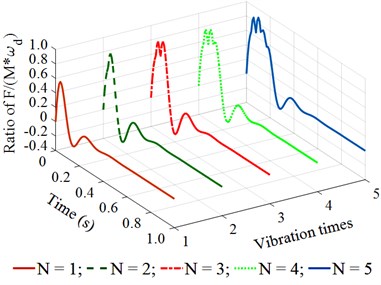
f) At an excitation frequency of 26 Hz

With $N=$ 5, the comparison results in Fig. 5 show that the remaining energy at 0.2 (s) of $f_c=$ 5, 10, and 14 Hz is quite low while both the compacting energy and the remaining energy at 0.2 (s) of $f_c=$ 18, 22, and 26 Hz are quite high. Therefore, based on the operating parameters of the asphalt pavers as the speed and vibration frequency, $N=$ 5 and $f_c=$ 18 to 22 Hz should be used to improve the compacting performance and the asphalt pavement density. To verify the numerical simulation results, the experimental study of the tamper-asphalt mixture interaction is performed as below.

Fig. 5The stimulating impulse response of the tamper-asphalt mixture interaction at N= 5 under the different excitations of the compacting mechanism

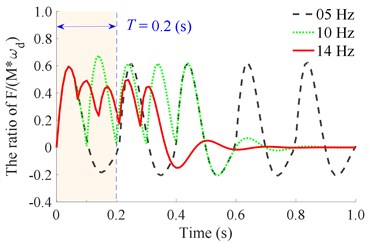
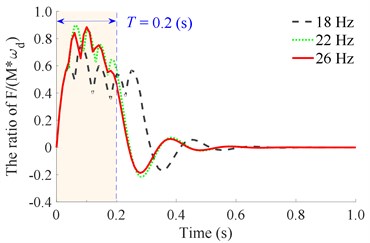
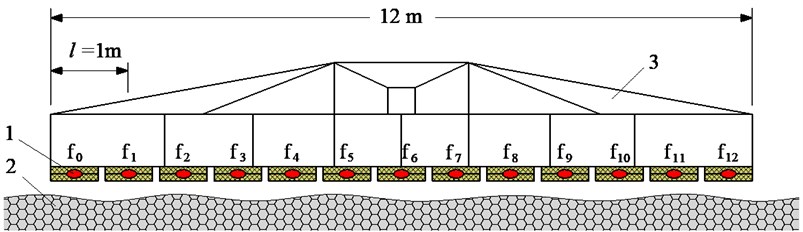
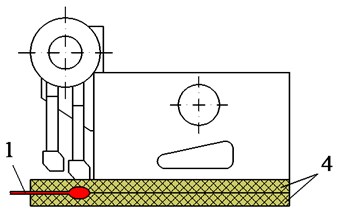
Fig. 6The experimental model of the tamper-asphalt mixture interaction: 1 – force sensor, 2 – asphalt pavement, 3 – compacting mechanism, 4 – two planks of hard rubber material

a) Front view of the compacting mechanism

b) Side view of the compacting mechanism

c) Model of force sensor setup

3.1. Experimental setup process

It is very difficult to measure the compressive force response of the tamper-asphalt mixture interaction in the actual condition due to the difficulty in determining the pressure and the compressive density of the compacted hot mix asphalt. To solve this issue, 13 pairs of hard rubber material sheets with their properties that are equivalent to that of hot mix asphalt are used to measure the compressive pressure and density of the tamper-asphalt mixture interaction, as shown in Figs. 6(a) and 7(a). At each pair of hard rubber material sheets installed below the compacting mechanism, a force sensor is installed in between two rubber plates, as plotted in Figs. 6(b), 6(c), and 7(b). The measured results are then computed and analyzed via the analysis system of Belgium LMS, as provided in Fig. 7(c).

Fig. 7The actual structure of the asphalt paver and its experimental setup process

a) Experimental setup of the compacting mechanism

b) Force sensor

c) Signal processor and display the results

Under the impact of the compacting force of the compacting mechanism in the vertical direction, the pressure $P$ distributed evenly on the upper surface of the rubber pad, accordingly, the displacements in the $x$ and $y$ directions of the pair of rubber pads are $u_x=u_y=$ 0 meanwhile the vertical displacements at upper and lower rubber pads are $u_z=h$ and $u_z=$ 0, as described in Fig. 6(c). Therefore, the displacement $W_z$ and stress ${\sigma }_z$ in the vertical direction at depth $z$ of the rubber pads are determined by [20]:

where $\nu$, $\rho$, and $E$ are e Poisson’s coefficient, density, and Young modulus of the rubber material, respectively.

At the installation position of the force sensor, the compressive stress of the rubber material has a linear relationship with the pressure $P$. Therefore, the pressure of the asphalt layer can be determined through the pressure in the rubber pads. The measurement process is then performed as below.

3.2. Discussion of the measured results

The measurement process is performed with $N=$ 5 under the different excitation frequencies of the compacting mechanisms $f_c=$ {5, 10, 18, and 22} Hz corresponding to two different excitation frequencies of the vibration screed $f_{screed}=$ {0 and 22.5} Hz. The experimental results of the stimulating impulse response and the compacting force distribution of compacting mechanisms on the asphalt pavement during the tamper-asphalt mixture interaction are plotted in Figs. 8 and 9, respectively.

Observing the comparison results between the measurement and simulation at the excitation frequencies of $f_c=$ 10 and 22 Hz with $N=$ 5 in Fig. 8(a) and 8(b), we can see that the curves of the stimulating impulse response between the measured and simulation results are similar. Therefore, the mathematical model and the numerical simulation result of the tamper-asphalt mixture interaction could be reliable.

Fig. 8The experimentation and simulation results of the stimulating impulse response of the tamper-asphalt mixture interaction at N= 5

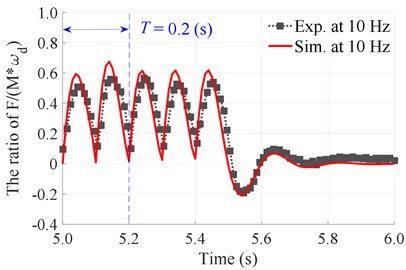
a) At an excitation frequency of 10 Hz

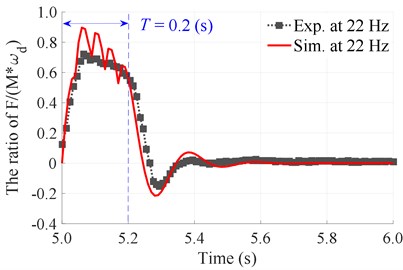
b) At an excitation frequency of 22 Hz

Fig. 9The experimental result of the compacting force distribution of compacting mechanisms during the tamper-asphalt mixture interaction

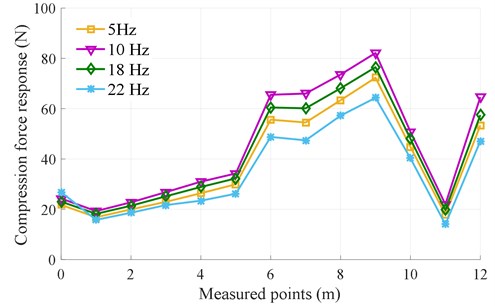
a) Without the excitation frequency of the screed, $f_{screed}=$ 0.0 Hz

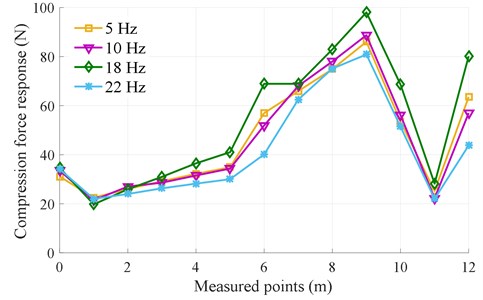
b) With 50 % of the excitation frequency of the screed, $f_{screed}=$ 22.5 Hz

Additionally, the results of the compacting force distribution of compacting mechanisms on the asphalt pavement in Fig. 9(a) without the excitation of the screed and Fig. 9(b) with using 50 % of the excitation of the screed show that the excitation frequency $f_c$ substantially affect the compacting force of the compacting mechanisms. In the case of ignoring the excitation of the screed ($f_{screed}=$ 0.0 Hz), the measured result in Fig. 9(a) indicates that the compacting force is increased with the increase of $f_c$ from 5 to 10 Hz, the compacting force is then reduced with the increase of $f_c$ from 18 to 22 Hz, and the maximum compacting force is obtained at $f_c=$ 10 Hz. Especially, the average value of the compacting force at $f_c=$ 10 Hz is increased by 22.54 % in comparison with that of $f_c=$ 22 Hz, as listed in Table 2.

In the case of the compacting mechanisms using 50 % of the excitation of the screed ($f_{screed}=$ 22.5 Hz), the measured result in Fig. 9(b) also is similar to that without the excitation of the screed in Fig. 9(a). However, the maximum compacting force is obtained at $f_c=$ 18 Hz. Particularly, the average value of the compacting force at $f_c=$ 18 Hz is increased by 21.05 % in comparison with that of $f_c=$ 22 Hz, as listed in the same Table 2. Besides, under the effect of the excitation frequency of the screed $f_{screed}$, the average values of the compacting force with using $f_{screed}=$ 22.5 Hz are higher than that without the excitation frequency of the screed. Especially, the maximum average value of the compacting force with using 50 % of the excitation of the screed is significantly increased by 21.19 % compared to that of without the excitation of the screed. This could be due to the influence of the vibration excitation of the screed. The maximum compacting force at $f_c=$ 18 Hz implies that the compression efficiency and asphalt density achieved are maximum. These measured results are similar to the results in Ref. [5]. Besides, the measured results in both Figs. 9(a) and 9(b) show that the compaction force responses at the measured points are remarkably skewed and asymmetrical, so the vibration screed system works are unstable and the paving quality is low. To solve this issue, the design parameters of the vibration screed system should be optimized to improve the paving performance of pavers.