Response spectrum method for spatial seismic ground motion

1. Introduction

The data from seismic arrays can show significant spatial variability of the seismic ground motion within small sites [1, 2]. The spatial variability can be considered in the earthquake-resistant design on the base of differential models of ground motion, with estimating seismic loads and obtaining seismic response by Response Spectrum Method (RSM) [3-6].

This paper presents a new modal approach to the seismic analysis of extended structures, when the spatial nature of the seismic excitation is taken into account. It includes a description of spatial differential motion for structural seismic analysis and calculation of seismic response of a structure using the RSM.

2. Differential seismic excitation

The differential seismic excitation is transferred to a structure as kinematic excitation of the ground base. The ground motion at the support points can be described three translational displacements. For structure with $p$ support points the ground motion at the $i$th point $\left(x_{1i},x_{2i},x_{3i}\right)$ is described by the vectors of absolute translational displacements, velocities, and acceleration ${\mathbf{X}}_i^{}\left(t,x_{1i},x_{2i},x_{3i}\right)={\left(\begin{array}{lll}{X}_{1i}^{}& X_{2i}^{}& X_{3i}^{}\end{array}\right)}^T\text{,}$${\dot{\mathbf{X}}}_i^{}\left(t,x_{1i},x_{2i},x_{3i}\right)={\left(\begin{array}{lll}{\dot{X}}_{1i}^{}& {\dot{X}}_{2i}^{}& {\dot{X}}_{3i}^{}\end{array}\right)}^T\text{,}$${\ddot{\mathbf{X}}}_i^{}\left(t,x_{1i},x_{2i},x_{3i}\right)={\left(\begin{array}{lll}{\ddot{X}}_{1i}^{}& {\ddot{X}}_{2i}^{}& {\ddot{X}}_{3i}^{}\end{array}\right)}^T$, $i=1,...,p$. The vector of translational accelerations at the $i$th point is equal to:

where $\left|{\ddot{\mathbf{X}}}_i^{}\right|=\sqrt{{\left({\ddot{X}}_{1i}^{}\right)}^2+{\left({\ddot{X}}_{2i}^{}\right)}^2+{\left({\ddot{X}}_{3i}^{}\right)}^2}$ – its magnitude, ${\mathbf{\nu }}_i^{}\left(t\right)={\left(\begin{array}{lll}{\nu }_{1i}^{}& {\nu }_{2i}^{}& {\nu }_{3i}^{}\end{array}\right)}^T$ – the vector of the directional cosines ${\nu }_{1i}^{}={\ddot{X}}_{1i}^{}/\left|{\ddot{\mathbf{X}}}_i^{}\right|$, ${\nu }_{2i}^{}={\ddot{X}}_{2i}^{}/\left|{\ddot{\mathbf{X}}}_i^{}\right|$, ${\nu }_{3i}^{}={\ddot{X}}_{3i}^{}/\left|{\ddot{\mathbf{X}}}_i^{}\right|.$

Peak translational accelerations at the $i$th point are equal to $I_i^{}=\mathrm{m}\mathrm{a}\mathrm{x}\left|{\ddot{\mathbf{X}}}_i^{}\right|$. For the modal RSM the vector ${\ddot{\mathbf{X}}}_i^{}$ and directional cosines of the seismic excitation are considered as constant:

The directions ${\mathbf{\nu }}_i^{}$ are found from maximum of the dynamic structural response and known as critical directions of the seismic excitation. The directions of the seismic loads applied to the structure are determined solely from its dynamic properties.

Spatial kinematic parameters at the different points is expressed in terms of the same parameters at the anchor point, for example, at the first point with displacements ${\mathbf{X}}_1^{}$ and accelerations ${\ddot{\mathbf{X}}}_1^{}$. According to Eq. (2), at the first point the accelerations are expressed in terms of the peak translational acceleration $I=I_1^{}$ and directional cosines ${\mathbf{\nu }}_1$: ${\ddot{\mathbf{X}}}_1^{}\left(x_1,x_2,x_3\right)=I{\mathbf{\nu }}_1$.

For the spatial kinematic field of accelerations, scalar matrix functions of coordinates are introduced. At the $i$th point with coordinates ${\mathbf{r}}_i=\left(x_{1i},x_{2i},x_{3i}\right)$:

Then three-dimensional vector of accelerations at the $i$th support point is written via peak acceleration at the anchor point (with regard to ${\ddot{\mathbf{X}}}_i^{}=I_i^{}\cdot {\mathbf{\nu }}_i^{}$) ${\ddot{\mathbf{X}}}_i^{}={\mathbf{{\rm T}}}_i^{}{\ddot{\mathbf{X}}}_1^{}=I{\mathbf{{\rm T}}}_i^{}{\mathbf{\nu }}_1$.

The $3p$ dimensional vector of accelerations $\ddot{\mathbf{X}}$ is equal to:

Amplification factors (AFs) can be different at different points of the spatial kinematic field. The ground motion at the $i$th support point is described by three-dimensional vector of spectral AFs ${\mathbf{\beta }}_i^{}\left(\mathrm{\Omega }\right)={\left(\begin{array}{lll}{\beta }_{1i}& {\beta }_{2i}& {\beta }_{3i}\end{array}\right)}^T$. At the anchor point ${\mathbf{\beta }}_1^{}\left(\mathrm{\Omega }\right)={\left(\begin{array}{lll}{\beta }_1& {\beta }_2& {\beta }_3\end{array}\right)}^T$, where $\mathrm{\Omega }$ is the natural frequency.

Functions ${\mathrm{\Theta }}_{ji}$ are introduced for describing of spatial spectral variation of seismic excitation ($j$ – the number of the accelerations vector component ${\ddot{\mathbf{X}}}_i^{}$, $j=\mathrm{1,2},3$; $i$ – the number of the support point, $i=1,...,p$). At the $i$th -support point with ${\mathbf{r}}_i=\left(x_{1i},x_{2i},x_{3i}\right)$ the AFs are equal:

or in matrix form ${\mathbf{\beta }}_i^{}\left(\mathrm{\Omega },{\mathbf{r}}_i\right)={\mathbf{\Theta }}_i\left(\mathrm{\Omega },{\mathbf{r}}_i\right){\mathbf{\beta }}_1^{}\left(\mathrm{\Omega }\right)$, where ${\mathbf{\Theta }}_i^{\left[3\times 3\right]}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\mathrm{\Theta }}_{1i},{\mathrm{\Theta }}_{2i},{\mathrm{\Theta }}_{3i}\right)$ – the matrix of spatial spectral functions relatively to the anchor point. All AFs at all support points are given by the vector $\mathbf{\beta }$: ${\mathbf{\beta }}^{\left[3p\right]}=\mathbf{\beta }\left(\mathrm{\Omega }\right)={\left(\begin{array}{lll}{\mathbf{\beta }}_1^{}& ...& {\mathbf{\beta }}_p^{}\end{array}\right)}^T$. Introduce the matrix of the spatial spectral functions ${\mathbf{\Theta }}^{\left[3p\times 3\right]}={\left({\mathbf{\Theta }}_1,{\mathbf{\Theta }}_2,...,{\mathbf{\Theta }}_p\right)}^T$, then the AFs at all support points are expressed about the anchor point ${\mathbf{\beta }}_1^{\left[3\right]}$: $\mathbf{\beta }=\mathbf{\Theta }{\mathbf{\beta }}_1^{}$.

3. Equations of motion

Consider a structure with $n$ degrees of freedom under multidimensional kinematic excitation transferred to the structure through $p$ support points. Denote ${\mathbf{q}}_{abs}^{\left[n\right]}$ – the vector of absolute generalized displacements, ${\mathbf{q}}^{\left[n\right]}$ – the vector of relative generalized displacements, ${\mathbf{q}}_{tr}^{\left[n\right]}$ – the vector of transport motion and:

The transport motion ${\mathbf{q}}_{tr}^{}$ is defined as displacements caused by the displacements $\mathbf{X}$ of all support points. Equations of absolute motion of the structure are:

where ${\mathbf{M}}_{}^{\left[n\times n\right]}$, ${\mathbf{B}}^{\left[n\times n\right]}$ and ${\mathbf{K}}^{\left[n\times n\right]}$ – the mass, damping and stiffness matrices, ${\mathbf{K}}_s^{\left[n\times 3p\right]}$, ${\mathbf{B}}_s^{\left[n\times 3p\right]}$– the stiffness and damping matrices of support elements, ${\mathbf{X}}_{}^{\left[3p\right]}$ and ${\dot{\mathbf{X}}}_{}^{\left[3p\right]}$ – the vectors of displacements and velocities of the ground at support points. From the equilibrium of the structure at the support points (${\dot{\mathbf{q}}}_{tr}^{\left[n\right]}$ – the vector of transport velocities):

Substituting Eq. (4) in Eq. (5) and considering Eq. (6) we get the equation of the relative motion:

For the case of small damping $\mathbf{K}{\mathbf{q}}_{tr}+{\mathbf{K}}_s\mathbf{X}\gg \mathbf{B}{\dot{\mathbf{q}}}_{tr}+{\mathbf{B}}_s\dot{\mathbf{X}}$, therefore from Eq. (6) $\mathbf{K}{\mathbf{q}}_{tr}+{\mathbf{K}}_s\mathbf{X}=0$. Denote the flexibility matrix $\mathbf{F}={\mathbf{K}}^{-1}$, then the transport motion vector is ${\mathbf{q}}_{tr}=-\mathbf{F}{\mathbf{K}}_s^{}\mathbf{X}$, and the equation of relative motion Eq. (7) has the form:

Denote the matrix of the transport inertial coefficients ${\mathbf{M}}_s^{\left[n\times 3p\right]}=-\mathbf{M}\mathbf{F}{\mathbf{K}}_s$, then Eq. (6) takes the ordinary form of the relative motion equation:

4. Structural seismic response

For solution of Eq. (8) is used modal analysis with orthogonal transformation $\mathbf{q}=\mathbf{V}\mathbf{u}$, where $\mathbf{u}$ – the vector of normal coordinates, $\mathbf{V}$ – the matrix of modes ${\mathbf{v}}_k$, $k=\mathrm{1,2},...,n$. Eq. (8) about normal coordinates is:

where ${\mathbf{\Omega }}_{}^2$ is the matrix of squares of natural frequencies, $\mathbf{Q}=-{\mathbf{M}}_{\mathrm{m}\mathrm{o}\mathrm{d}}^{-1}{\mathbf{V}}^T{\mathbf{M}}_{\mathbf{s}}\ddot{\mathbf{X}}$ – the vector of transport seismic forces. Considering Eq. (3), $\mathbf{Q}=-I{\mathbf{M}}_{\mathrm{m}\mathrm{o}\mathrm{d}}^{-1}{\mathbf{V}}^T{\mathbf{M}}_{\mathbf{s}}\mathbf{{\rm T}}\mathbf{\nu }$, ${\mathbf{M}}_{\mathrm{m}\mathrm{o}\mathrm{d}}={\mathbf{V}}^T\mathbf{M}\mathbf{V}$.

From Eq. (9) static modal displacement is $u_k^{st}=-\frac{I}{M_{\mathrm{m}\mathrm{o}\mathrm{d},k}{\mathrm{\Omega }}_k^2}{\mathbf{v}}_k^T{\mathbf{M}}_{\mathbf{s}}\mathbf{T}{\mathbf{\nu }}_k$, where ${\mathbf{\nu }}_k$ – the vector of critical directions of seismic excitation for the $k$th mode, $M_{\mathrm{m}\mathrm{o}\mathrm{d},k}={\mathbf{v}}_k^T\mathbf{M}{\mathbf{v}}_k^{}$ – the modal mass for the $k$th mode. Dynamic modal displacements for the $k$th mode is obtained as a product of $u_k^{st}$ and ${\beta }_k$: $u_k^{}=-\frac{{\beta }_{k}I}{M_{\mathrm{m}\mathrm{o}\mathrm{d},k}{\mathrm{\Omega }}_k^2}{\mathbf{v}}_k^T{\mathbf{M}}_{\mathbf{s}}\mathbf{T}{\mathbf{\nu }}_k$.

Structural seismic response $\mathbf{S}$ can be decompose by the sum of modal responses ${\mathbf{S}}_k$:

$\mathbf{S}=\mathbf{K}\mathbf{q}=\sum _{k=1}^n{u}_k\mathbf{K}{\mathbf{v}}_k=\sum _{k=1}^n{u}_k{\mathrm{\Omega }}_k^2\mathbf{M}{\mathbf{v}}_k=\sum _{k=1}^n{\mathbf{S}}_k$, where ${\mathbf{S}}_k=u_k{\mathrm{\Omega }}_k^2\mathbf{M}{\mathbf{v}}_k$ – the vector of modal response corresponding to the $k$th mode. If ${\mathbf{m}}_i^{\left[n\right]}$$\left(i=1,...,n\right)$ is the $i$th row of the mass matrix $\mathbf{M}$, and $i$th element of ${\mathbf{S}}_k$ is $S_{ik}={\beta }_{k}I{\mathbf{m}}_i\frac{{\mathbf{v}}_k{\mathbf{v}}_k^T{\mathbf{M}}_{\mathbf{s}}}{M_{\mathrm{m}\mathrm{o}\mathrm{d},k}}\mathbf{T}{\mathbf{\nu }}_k$.

5. Research and testing

To test the method, we perform calculations of many types of structures, both very simple [4, 5] and real complex models of structures under various types of earthquakes.

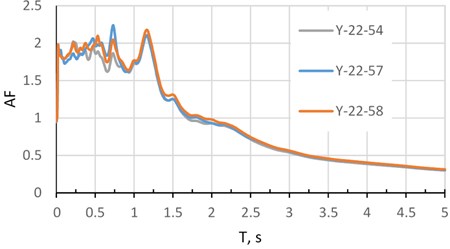
A good example for studying the effect of spatial seismic variability on the dynamic response is a stadium cover model in Fig. 1, which has 8 main supports arranged in a circle with a diameter of 250 m. The range of natural frequencies taken for seismic analysis is 0.13-1.45 Hz, in natural periods 0.7-7.7 s. The ground accelerations at each support are different. To determine the differential ground motion, we have records of two weak natural earthquakes recorded at one of industrial sites [7] at points with distances between them of 150-200 m. A soil is composed of sand and clay layers. A shear waves velocity at near-surface is 230-300 m/s. A seismic event No. 10 is local, short and more high-frequency; an event No. 22 is regional, long and more low-frequency. In Fig. 2 and 3 are shown the amplification factors (AF) of both earthquakes depending on natural periods $T$ for one of horizontal components (direction $Y$).

Fig. 1Finite element model of the stadium cover

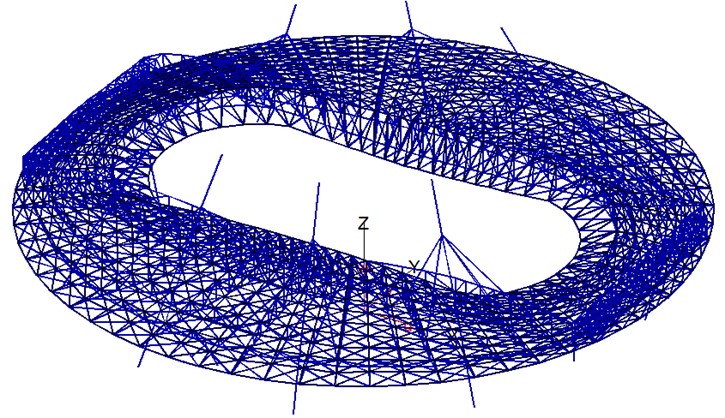
Table 1 shows the standard deviations (SD) of accelerations for both events for each of the three directions at points 54, 57, and 58. These points are located on a flat site at the vertices of an almost equilateral triangle with sides of about 175 m.

Both events demonstrate a significant variability of the acceleration field, more expected for a short-wave event No. 10. In Table 1 the difference between the maximum and minimum SD reaches almost 27 % for event No. 10 and almost 32 % for event No. 22; it indicates the need to apply seismic analysis based on a differential model of ground motion.

Usually, an earthquake engineering of many wide structures is assumed identical ground motion at all support points and using only one accelerogram. Comparing the seismic loads calculated in the traditional way with the loads obtained by the proposed method, we can make brief conclusions: spatial seismic impact leads to a different distribution of seismic loads and internal forces, to a significant increase of seismic loads on some structural elements, to other mechanisms of damage accumulation and destruction.

Fig. 2Amplification factors. Earthquake 10 at points 54, 57, 58, direction Y

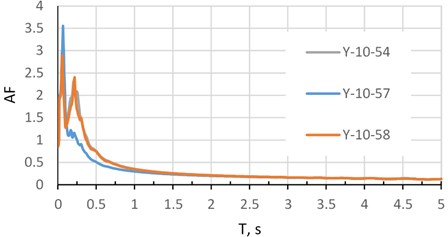
Fig. 3Amplification factors. Earthquake 22 at points 54, 57, 58, direction Y

6. Conclusions

The paper presents modified RSM that is applied for differential seismic analysis of structures. This method works reliably for random unpredictable wave processes at the base, considering the worst possible situations, for example, the motion of different supports in opposite phases.

Currently, the proposed method is being tested on real large complex objects, a dependence between structural response and variability of spatial seismic ground motion is investigated, new software is developed and put into practice.

The results of this work can be applied in new seismic standards.