Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries

Tang, Zhiyin; Zou, Hailong; Shen, Huijie; Wu, Shasha

doi:10.21595/vp.2021.22229

Vibroengineering Procedia

Browse Procedia

Published: 02 December 2021

Check for updates

Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries

Zhiyin Tang¹

Hailong Zou²

Huijie Shen³

Shasha Wu⁴

^{1, 2, 3}College of Power Engineering, Naval University of Engineering, Wuhan, Hubei, 430033, China

⁴Zhongnan University of Economics and Law, Wuhan, Hubei, 430073, China

Corresponding Author:

Huijie Shen

Cite the article Download PDF

Downloads 571

Abstract

The concept of underwater vehicle auxiliary machineries acoustic fault was proposed. The underwater vehicle auxiliary machineries acoustic fault diagnosis in concealed conditions was studied. Firstly, the accelerometers were used to measure the vehicle shell surface vibration, and the vehicle radiation noise was calculated using a rapid engineering estimation method. Then, the vibration energy of each frequency band in the radiation noise analysis frequency was extracted as feature vector. Finally, an improved Fuzzy Support Vector Machine (FSVM) method was used to identify the classification, and acoustic fault diagnoses of auxiliary machineries for underwater vehicle was given. The method of acoustic fault diagnosis proved a theoretical basis for the use of underwater vehicle auxiliary machineries under the concealment.

Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries

Highlights

The concept of underwater vehicle auxiliary machineries acoustic fault has been proposed.
The vehicle radiation noise was calculated using a rapid engineering estimation method.
An improved Fuzzy Support Vector Machine (FSVM) method was used to identify the classification, and acoustic fault diagnoses of auxiliary machineries for underwater vehicle was given.

1. Introduction

The stealth property of underwater vehicle in sea battlefield is the most basic technical performance, where acoustic stealth performance is the most important factor in determining its stealth. The s acoustic stealth performance of underwater vehicle has always been considered to be the most important issue [1]-[4].

The radiation noise of underwater vehicle can be divided into three kinds: machineries noise, propeller noise, hydrodynamic noise [5]. When the underwater vehicle is sailing, the propeller noise and the hydrodynamic noise occupy the main part. But when it is in concealed conditions such as “position for ambush”, “regional hunting” and so on, underwater vehicle should be in hover condition. And in these time, the host and propeller are both stopped. The propeller noise and the hydrodynamic noise disappear, and the radiation noise of the vehicle is only the mechanical noise. At these times, the main noise sources are auxiliary machineries, which mainly includes various types of pumps, air conditioners, refrigeration, hydraulic devices and so on. Now if the radiation noise is abnormal due to the incorrect use of auxiliary machineries, the acoustic stealth performance of the vehicle is changed, and its security is destroyed. This is called the acoustic fault of auxiliary machineries.

Define “underwater vehicle auxiliary machineries acoustic fault” as: in sea battlefield, when underwater vehicle auxiliary machineries vibration or noise changes due to improper use or state change, resulting in changing vehicle stealth properties. It should be noted that the auxiliary mechanical acoustic fault does not mean that the auxiliary machineries has a mechanical fault and needs to be repaired.

“Underwater auxiliary mechanical acoustic fault diagnosis” is: when the underwater vehicle auxiliary machineries are mainly used, the current acoustic stealth state elements are perceived and extracted, and they map them into existing state spaces, get some kind the matching of known states, and determines its acoustic fault state. The state here can be quantized indicators (like 60 points, 90 points, etc.), or may be a hierarchical evaluation (like no acoustic fault, slight acoustic fault, severe acoustic fault, etc.).

It should be noted that underwater vehicle auxiliary mechanical acoustic fault diagnosis is mainly carried out under hover condition or slow sailing. Because in these time vehicle has higher requirements for stealth, and machineries noise is the main part of radiation noise. When the vehicle is at a high speed, the maneuverability requirement is higher than stealth. In these time, the propeller noise and hydrodynamic noise are much louder than machineries noise, so the auxiliary mechanical acoustic fault diagnosis is not necessary.

2. Rapid calculation method of underwater vehicle radiation noise in concealed conditions

The first step in the diagnosis is to quickly calculate the radiation noise, which is made by auxiliary machineries, by using the vibration measured by the sensors on the vehicle. An engineering estimation method of rapid calculating underwater vehicle radiation noise in concealed conditions has been proposed [6], [7]. The radiation noise is [7]:

1

P = \frac{ρ_{0} c_{0} ⟨\bar{V}⟩}{2 R} \sqrt{\frac{ε S}{π}} = \frac{ρ_{0} c_{0} ⟨\bar{ζ}⟩}{2 ω R} \sqrt{\frac{ε S}{π}},

where, $P$ is the sound pressure of radiation noise at a distance of $R$ from the vehicle; $ρ_{0}$ , $c_{0}$ are the density and sound speed of water; $⟨\bar{V}⟩$ is the average vibration speed of the vehicle surface; $⟨\bar{ζ}⟩$ is the average vibration acceleration of the vehicle surface; $S$ is the acoustic radiation surface area of the vehicle; $ε$ is the radiation efficiency of the vehicle:

2

10 l g ε = \{\begin{array}{l} 40 (l g f - l g f_{m}), f \leq f_{1}, \\ 20 (1 + K) l g f + 20 (1 - K) l g f_{1} - 40 l g f_{m}, f_{1} < f < f_{c}, \\ 0, f \geq f_{c}, \end{array}

where, $f$ is a calculation frequency; $K = \frac{l g (f_{m}^{2}) / (f_{c} f_{1})}{l g (f_{c} f_{1})}$ ; $f_{1}$ is the first order of vibration modal frequency of the cylindrical vehicle:

3

f_{1} = \{\begin{array}{l} 2.66 f_{r} β, {(\frac{d}{l})}^{2} \geq 0.6 (\frac{h}{d}), \\ \frac{π d f_{r}}{2 l} \sqrt{{(\frac{π d}{2 l})}^{2} + 2 β^{2}}, {(\frac{d}{l})}^{2} < 0.6 (\frac{h}{d}) . \end{array}

Critical frequency $f_{c}$ is:

4

f_{c} = \frac{{c_{0}}^{2}}{2 π h} \sqrt[]{\frac{12 ρ (1 - σ^{2})}{E}} = \frac{2 \sqrt{3} R_{c p}}{h} {(\frac{c_{0}}{c_{l}})}^{2} f_{r} .

In the real underwater vehicle radiation noise calculation, lots of accelerometers are arranged on the surface of the vehicle. The sound pressure of each cabin is considered independent. The length of $i$ -th cabin is $l_{i}$ , and the equivalent radius is $r_{i}$ . It can be obtained from Eqs. (1-4) that the total sound pressure, which is made by the underwater vehicle multi-cabin vibration, at a distance of $R$ from the vehicle is $P_{\sum} = \sum_{i} \frac{ρ_{0} c_{0} ⟨\bar{ζ}⟩}{ω R} \sqrt{\frac{ε_{i} r_{i} l_{i}}{2}}$ .

Translates to the total sound pressure at a distance of 1m from the vehicle is:

5

P_{\sum} = \sum_{i} \frac{ρ_{0} c_{0} ⟨\bar{ζ}⟩}{ω} \sqrt{\frac{ε_{i} r_{i} l_{i}}{2}} .

If the energy of radiation noise is mostly concentrated from $f_{d o w n}$ to $f_{u p}$ frequency range, each 1/3Oct sound pressure levels of the frequency range can be arranged to the feature vectors.

Using this underwater vehicle radiation feature vectors, the pattern recognition can be performed by the fuzzy support vector machine (FSVM) to make the auxiliary mechanical acoustic fault diagnosis.

3. FSVM for diagnosis of two modes

If the auxiliary machine acoustic fault category is simple to be two: occurring and not occurring, the acoustic fault diagnosis problem is an identification issue of two model classes. Under the conditions of complete linearity, ordinary linear support vector machines (SVM) are suitable for this problem [8]. However, in actual underwater vehicle auxiliary machineries acoustic fault diagnosis, the sample is almost not completely linear, so the nonlinear SVM must be used. And sometimes, not all training samples are valid. Some the validity of samples may be weakened or even be corrupted in actual underwater vehicle auxiliary machineries acoustic fault diagnosis. For such problems, the FSVM method has been proposed [9], [10].

3.1. Linear FSVM for diagnosis of two patterns

In order to solve non-separable data, a set of new non-negative scalar variables $ξ_{i} (i = 1,2, \dots, l)$ are introduced to the definition of the separation super plane:

6

y_{i} (w^{T} x_{i} + b) \geq 1 - ξ_{i}, i = 1,2, \dots, l,

where, $ξ_{i}$ is a relaxation variable, which measures the data deviation degree of the ideal condition of separable pattern. Support vector is the special data that exactly satisfied Eq. (6). For linear classification problems, the problem of searching for the optimal classification super plane can be transform to solve the Eq. (7):

7

\{\begin{array}{l} m i n i m i z e \frac{1}{2} {‖w‖}^{2} + C \sum_{i = 1}^{l} s_{i} ξ_{i}, \\ s u b j e c t t o \begin{array}{l} y_{i} (w^{T} x_{i} + b) \geq 1 - ξ_{i}, i = 1,2, \dots l, \\ ξ_{i} \geq 0, i = 1,2, \dots l . \end{array} \end{array}

That is, a fault classification support vector with a smaller degree of fuzzy membership is considered less important in the classification problem. The Lagrange multiplier method can be used to solve this optimization problem. Constructing the Lagrange function as:

8

L (w, b, ξ, α, β) = \frac{1}{2} {‖w‖}^{2} + C \sum_{i = 1}^{l} s_{i} ξ_{i} - \sum_{i = 1}^{l} α_{i} (y_{i} (w^{T} x_{i} + b) - 1 + ξ_{i}) - \sum_{i = 1}^{l} β_{i} ξ_{i} .

The solution to the optimization problem is determined by the saddle points of the Lagrange function. When the cost function $\frac{1}{2} {‖w‖}^{2} + C \sum_{i = 1}^{l} s_{i} ξ_{i}$ takes the extreme value, by Karush-Kuhn-Thcker condition. The dual programming of the quadratic programming Eq. (7) can be converted to solving for the minimum as:

9

\{\begin{array}{l} \underset{α}{m i n i m i z e} \frac{1}{2} \sum_{i = 1}^{l} \sum_{j = 1}^{l} y_{i} y_{j} α_{i} α_{j} ({x_{i}}^{T} x_{j}) - \sum_{i = 1}^{l} α_{i}, \\ s u b j e c t t o \begin{array}{l} \sum_{i = 1}^{l} y_{i} α_{i} = 0, \\ 0 \leq α_{i} \leq s_{i} C, i = 1,2, \dots l . \end{array} \end{array}

The optimal solution of $w$ and $b$ are:

10

w^{*} = \sum_{i = 1}^{l} α_{_{i}}^{*} y_{i} x_{i},

11

b^{*} = y_{i} - \sum_{j = 1}^{l} y_{j} α_{j} ({x_{j}}^{T} x_{i}), i \in \{i |0 < α_{i}^{*} < s_{i} C|\} .

The fuzzy optimal classification function is:

12

g (x) = s g n \{f (x)\} = s g n \{(w^{* T} x) + b^{*}\}, x \in R^{n} .

3.2. Nonlinear FSVM for diagnosis of two patterns

For nonlinear classification issues, it is usually used by nonlinear mapping from low dimensional spaces to high dimension $φ (\cdot) : R^{d} \to R^{d h}$ , and transforms nonlinear problems in low dimensional spaces into linear problems in high dimensional spaces. Inner product operation in high dimensional space is defined as $K (x_{i}, x_{j}) = φ {(x_{i})}^{T} φ (x_{j})$ , and it is called kernel function [11]. So the issues of seeking the optimal classification hyperplane can be transformed to solving the quadratic programming. The solution process is the same as in Section 2.1, and the following dual planning can be obtained:

13

\{\begin{array}{l} \underset{α}{m i n i m i z e} \frac{1}{2} \sum_{i = 1}^{l} \sum_{j = 1}^{l} y_{i} y_{j} α_{i} α_{j} K (x_{i}, x_{j}) - \sum_{i = 1}^{l} α_{i}, \\ s u b j e c t t o \begin{array}{l} \sum_{i = 1}^{l} y_{i} α_{i} = 0, \\ 0 \leq α_{i} \leq s_{i} C, i = 1,2, \dots l . \end{array} \end{array}

Similarly, the optimal solution is $α^{*} = {(α_{1}^{*}, α_{2}^{*}, \dots, α_{l}^{*})}^{T}$ , and the fuzzy optimal classification function is:

14

g (x) = s g n \{f (x)\} = s g n \{\sum_{j = 1}^{l} α_{_{j}}^{*} y_{j} K (x, x_{j}) + b^{*}\}, x \in R^{n} .

where $b^{*} = y_{i} - \sum_{j = 1}^{l} y_{j} α_{j} K (x_{j}, x_{i})$ , $i \in \{i |0 < α_{i}^{*} < s_{i} C|\}$ .

Polynomial function, radial basis function, sigmoid function are often used as kernel functions. To a specific problem, how to choose the optimal kernel function and the corresponding parameters are a complex problem to FSVM. Although the choice of kernel functions can lead to different performances, the choice of parameters is more important than the choice of kernel functions. In many cases, the choice of the kernel function parameters is decisive to the result [11].

4. FSVM for diagnosis of multi-patterns

In the actual underwater vehicle auxiliary machineries acoustic fault diagnosis, the acoustic fault patterns are usually more than two. So underwater vehicle auxiliary machineries acoustic fault diagnosis is a multi-pattern classification problem. For more than two patterns ( $n > 2$ ), it can be constructed as a combination of multiple two-pattern classification issues [12]-[13].

Using two patterns classification methods, $n$ -pattern classifier can be constructed as follow:

1. Construct $n$ two-pattern classification rules, where the rule $f_{k} (x)$ , $k = 1, \dots, n$ separates the training samples of the $k_{t h}$ -pattern from other training samples. (If the vector $x_{i}$ belongs to the $k_{t h}$ -pattern, $g_{k} (x_{i}) = s g n \{f_{k} (x_{i})\} = 1$ ; otherwise $g_{k} (x) = s g n \{f_{k} (x_{i})\} = - 1$ ).

2. If the patterns satisfy $g_{k} (x) = s g n \{f_{k} (x)\} = 1$ are more than one, $x$ becomes the pattern $m = a r g m a x \{f_{1} (x), \dots f_{k} (x)\}$ that is corresponding to the maximum value of the function $f_{k} (x), k = 1, \dots, n$ . If all the patterns satisfy $g_{k} (x) = s g n \{f_{k} (x)\} = - 1$ , $x$ becomes the pattern $m = a r g m i n \{f_{1} (x), \dots f_{k} (x)\}$ that is corresponding to the minimum value of the function $f_{k} (x), k = 1, \dots, n$ .

5. Test verification

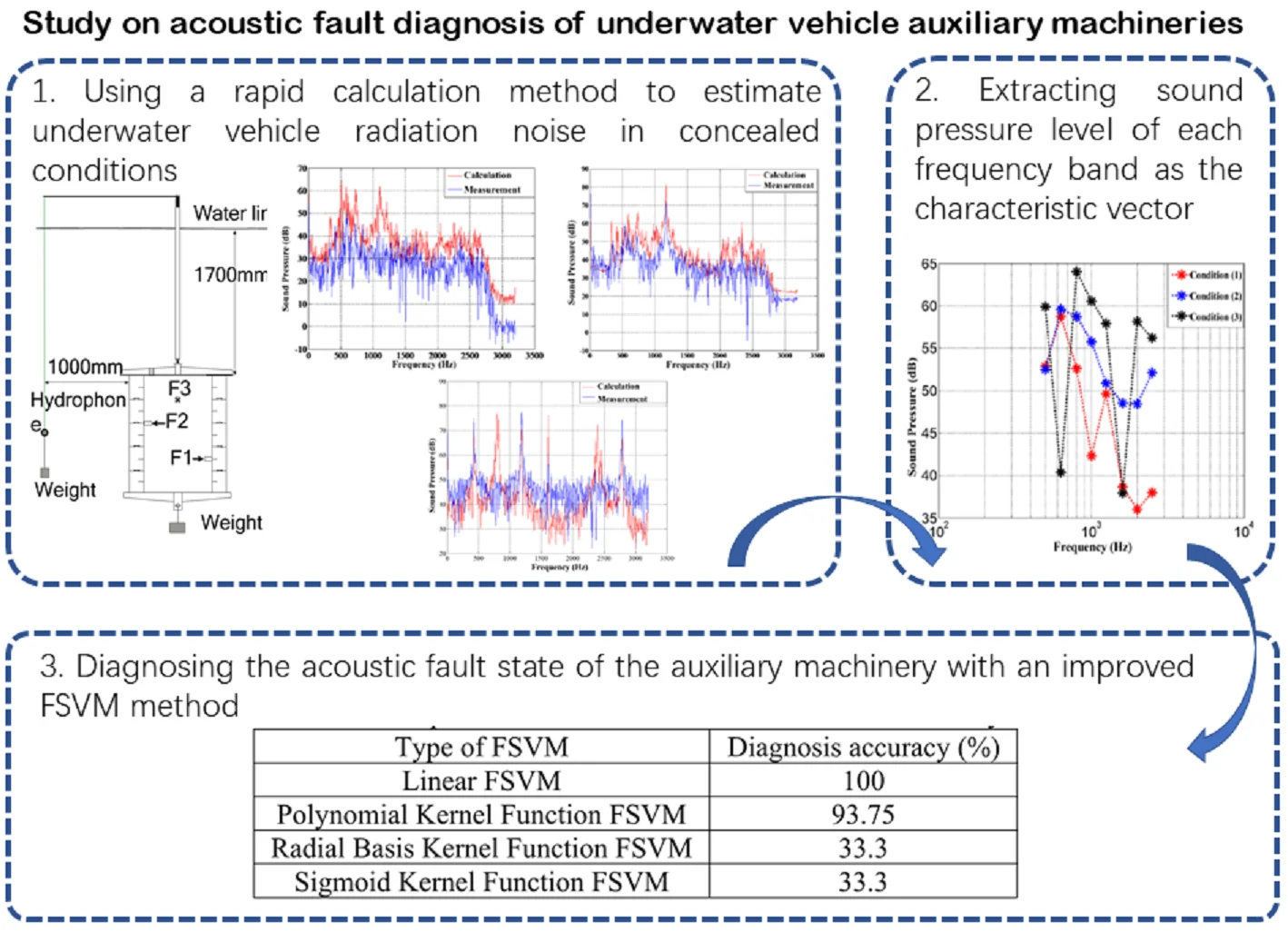
In order to verify the FSVM diagnosis method, underwater acoustic tests are performed using a double-shell iron cylinder to simulate underwater vehicle under hover condition. The outer diameter of the cylinder is 560 mm, the inner diameter is 400 mm, and the height is 600 mm. Three exciters are mounted inside the housing to simulate the excitation of the auxiliary mechanicals, and 15 accelerometers are arranged on the surface of the cylinder, as shown in Fig. 1. A hydrophone suspended in the water is 1m from the cylinder, as shown in Fig. 2.

Fig. 1Iron cylinder with covers and accelerometers, F1, F2, F3 are the excitation points of exciters

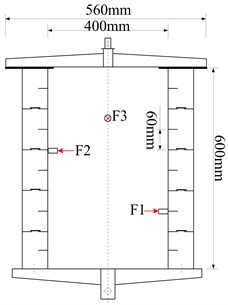
Fig. 2Underwater acoustic test

Without loss of generality, the auxiliary mechanical acoustic fault states can be classified into three patterns for diagnosis, namely: safety, normal fault, critical fault. They correspond to three conditions in the test: Condition (1) turn on No. 1 exciters, Condition (2) turn on No. 1 and 2 exciters, Condition (3) turn on all the three exciters.

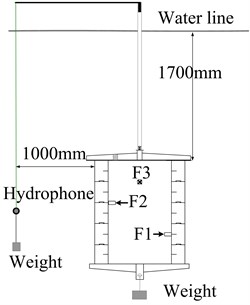
To verify the correctness of the algorithm in Chapter 1, a random set of data is selected for calculation in each condition. And calculation results are compared with the hydrophone measurement, as shown in Fig. 3-5.

As Table 1 shows, for our test linear FSVM and polynomial kernel function FSVM gets high accuracy in acoustic fault diagnosis. This is because the system is largely linear. However, the actual underwater vehicle has so many different kinds of auxiliary machineries, and underwater environment is so complicated, that the system cannot be considered as linear. So it is impossible to predict which type of FSVM will give better diagnosis results.

Fig. 3Comparison in Condition (1)

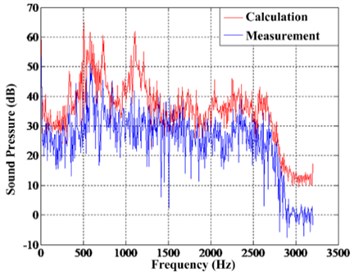
Fig. 4Comparison in Condition (2)

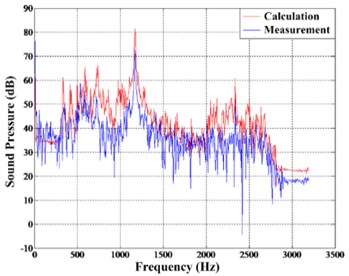
Fig. 5Comparison in Condition (3)

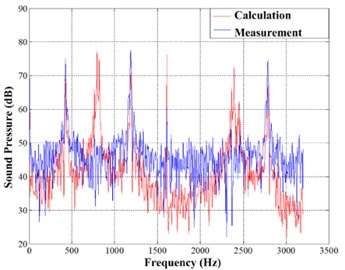
Fig. 6Each band sound pressure in three conditions

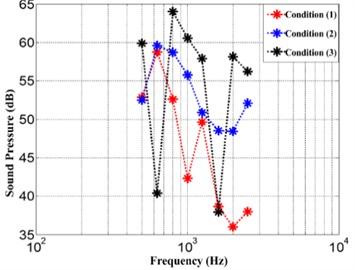
Table 1Comparison of different FSVM classification accuracy

Type of FSVM	Diagnosis accuracy (%)
Linear FSVM	100
Polynomial Kernel Function FSVM	93.75
Radial Basis Kernel Function FSVM	33.3
Sigmoid Kernel Function FSVM	33.3

6. Conclusions

In the paper the concept of underwater vehicle auxiliary machineries acoustic fault has been proposed, and the auxiliary machineries acoustic fault diagnosis in sea battlefield has been studied. It should be noticed that: (1) for different underwater vehicle structures, the FSVM classifier needs to be trained with historical data; (2) in actual underwater vehicle auxiliary machineries acoustic fault diagnosis, the selection of FSVM classifier kernel function should be according to the situation; (3) as the auxiliary machineries acoustic fault patterns increase, the amount of FSVM calculation will increase rapidly, which increases the diagnosis time; (4) the noise prediction accuracy of the underwater vehicle radiation noise engineering estimation algorithm needs to be improved in individual frequency bands.

References

He Lin, “Development of submarine acoustic stealth technology,” Ship Science and Technology, Vol. 28, pp. 9–17, 2006.

Search CrossRef
Sun Weihong and Yan Xin, “Some progress of the research of vibration and noise control technology for submarine,” Noise and Vibration Control, Vol. 5, pp. 6–10, 2012.

Search CrossRef
Su Qiang, Wang Guibo, and Zhu Pengfei, “Summarize of foreign submarine acoustic stealth frontier technologies development,” Ship Science and Technology, Vol. 36, No. 1, pp. 1–9, 2014.

Search CrossRef
Chen Zhijian, Xia Qiqiang, and Ai Haifeng, “Review of vibro-acoustic characteristics of submarine and advances in acoustic design,” Noise and Vibration Control, Vol. 2, pp. 1–6, 2012.

Search CrossRef
Robert J. Urick, Principles of Underwater sound. New York: McGraw Hill Inc., 1983.

Search CrossRef
He Ynanan and Yang Desen., “Experiment study of predicting method for radiating noise by submerged vibrating structure,” Journal of Ship Mechanics, Vol. 3, No. 2, pp. 58–62, 1999.

Search CrossRef
Shi Shengguo, Yang Desen, and He Yuanan., “Engineering estimation of noises from submerged structures,” Journal of Harbin Engineering University, Vol. 23, No. 1, pp. 91–94, 2002.

Search CrossRef
Ding Shifei, Qi Bingjuan, and Tan Hongyan, “An overview on theory and algorithm of support vector machines,” Journal of University of Electronic Science and Technology of China, Vol. 40, No. 1, pp. 2–10, 2011.

Search CrossRef
Chun-Fu Lin and Sheng-De Wang, “Fuzzy support vector machines,” IEEE Transactions on Neural Networks, Vol. 13, No. 2, pp. 464–471, Mar. 2002, https://doi.org/10.1109/72.991432

Publisher
Shigeo Abe and Takuya Inoue, “Fuzzy support vector machines for multiclass problems,” in ESANN 2002, 10th Eurorean Symposium on Artificial Neural Networks, Bruges, Belgium, April 24-26, 2002, Proceedings, pp. 113–118, Jan. 2002.

Search CrossRef
Feng Guohe, “Parameter optimizing for support vector machines classification,” Computer Engineering and Applications, Vol. 47, No. 3, pp. 123–128, 2011.

Search CrossRef
Andrew R. Webb and Keith D. Copsey, Statistical Pattern Recognition. Southern Gate: John Wiley & Sons Ltd., 2011.

Search CrossRef
Vladimir N. Vapnik, Statistical Learning Theory. Beijing: Publishing House of Electronics Industry, 2004.

Search CrossRef

About this article

Received

29 September 2021

Accepted

20 October 2021

Published

02 December 2021

SUBJECTS

Acoustics, noise control and engineering applications

DOI

https://doi.org/10.21595/vp.2021.22229

Keywords

underwater vehicle auxiliary machineries

acoustic fault diagnosis

FSVM

Acknowledgements

This research was funded by the Foundation of National Key Laboratory of Science and Technology (Grant No. 6142217200505), the Independent Research Foundation of Naval University of Engineering (Grant No. 20200290).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 08 06

Study on wake field and noise of underwater solid rocket engine

Xiaohui He, Zhongle Liu, Zhiyong Yuan, Xianyong Wang

Research article

2018 10 19

The influence of large foundation arrangement on underwater radiated noise of underwater vehicle engine compartment

Xu Zhiyun, Liu Chaojun, Peng Weicai

Research article

2018 09 24

Position error estimation of the underwater coordinate measurement machine using artificial neural network

Soji Shimono, Yuki Hagino, Uichi Nishizawa, Shigeki Toyama

Research article

2017 10 21

Fault diagnosis of electro-mechanical actuator based on WPD-STFT time-frequency entropy and PNN

Jiayao Jing, Hongmei Liu, Chen Lu

Z. Tang, H. Zou, H. Shen, and S. Wu, “Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries,” Vibroengineering PROCEDIA, Vol. 39, pp. 94–100, Dec. 2021, https://doi.org/10.21595/vp.2021.22229

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2021.22229
UR  - https://doi.org/10.21595/vp.2021.22229
TI  - Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries
T2  - Vibroengineering PROCEDIA
AU  - Shen, Huijie
AU  - Tang, Zhiyin
AU  - Zou, Hailong
AU  - Wu, Shasha
PY  - 2021
DA  - 2021/12/02
PB  - JVE International Ltd.
SP  - 94-100
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Shen_2021,
	doi = {10.21595/vp.2021.22229},
	url = {https://doi.org/10.21595/vp.2021.22229},
	year = 2021,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	pages = {94--100},
	author = {Huijie Shen and Zhiyin Tang and Hailong Zou and Shasha Wu},
	title = {Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]H. Shen, Z. Tang, H. Zou, and S. Wu, “Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries,” Vibroengineering PROCEDIA, pp. 94–100, Dec. 2021, doi: 10.21595/vp.2021.22229.

Copy IEEE

Copied to clipboard!

Shen, Huijie, Zhiyin Tang, Hailong Zou, and Shasha Wu. “Study on Acoustic Fault Diagnosis of Underwater Vehicle Auxiliary Machineries.” Vibroengineering PROCEDIA, December 2, 2021, 94–100. https://doi.org/10.21595/vp.2021.22229.

Copy Chicago

Copied to clipboard!

Study on acoustic fault diagnosis of underwater vehicle auxiliary machineries

Abstract

Highlights

1. Introduction

2. Rapid calculation method of underwater vehicle radiation noise in concealed conditions

3. FSVM for diagnosis of two modes

3.1. Linear FSVM for diagnosis of two patterns

3.2. Nonlinear FSVM for diagnosis of two patterns

4. FSVM for diagnosis of multi-patterns

5. Test verification

6. Conclusions

References

About this article

Related Articles