An efficient coupling algorithm of fluid structure interaction for marine propeller flow

1. Introduction

A propeller vibrates due to the excitation of the transient hydrodynamic force when it works under water. The vibration of the propeller induces movement of the fluid around the propeller and influences the propeller flow. On the other hand, the flow field variation changes the transient hydrodynamic force of the propeller and affects its vibration. This kind of fluid structure interaction of the propeller causes fluid noise, vibration noise of the propeller blade and even radiation noise through activating the hull vibration. It is detrimental to the acoustic stealthy of ships [1]. As the diameter of propellers becomes larger, the rotational speed and noise lower, the stiffness of propellers reduces. For insistence, the vibration amplitude of a composite propeller induced by flow is 5 times the vibration amplitude of a traditional nickel copper alloy propeller [2]. The stiffness reduction of the propeller makes the fluid structure interaction more and more important. Therefore, it is necessary to research and resolve the fluid structure interaction issues of propellers.

Accurate and reliable fluid structure coupling algorithms are essential for the research of the fluid structure interaction issues of propellers. The computational accuracy of fluid structure coupling algorithms based on CFD/CSD in which the flow is viscous is high. This coupling algorithm was applied in the study of the fluid structure interaction of propellers. In 2012, He [3] calculated the propeller vibration induced by ship wake inflow using a fluid structure coupling algorithm based on CFD/CSD. The computational efficiency of fluid structure coupling algorithms is usually low [4] because of the iterative calculations of the flow and the flow dynamic mesh of which the freedom quantity is always above 1 million for every time step. The computing time can be reduced by 50 % with a fast dynamic mesh method proposed by the present author of this paper in 2017 [5], [6]. The fast dynamic mesh method can just accelerate the calculation of the flow mesh deformation. The iterative computations for the flow are still computationally expensive in actual fluid structure coupled computations. In this paper, the above fast dynamic mesh method is applied in the research of the fluid structure interaction issue of propellers and an efficient coupling algorithm has been developed to reduce the computing time of fluid structure coupled computations based on CFD/CSD furthermore for propellers through iterative computations called single-loop iterations between flow, propeller vibration and flow dynamic mesh.

2. Control equations of flow based on dynamic mesh

The control equations of flow based on dynamic mesh for fluid structure interactions can be derived by transferring the traditional equations into ALE coordinates. The N-S equations in ALE coordinates is written as below:

where $u$, $v$, $w$ is the velocity component of the velocity vector in the $x$, $y$, $z$ direction apparently; $\mu$ is the dynamic viscosity of water; $p$ is the pressure of water; $S_u$, $S_v$, $S_w$ are the generalized source terms.

Therefore, the turbulence equations of the RNG $k$-$\epsilon$ model is adopted to close the control equations of flow in this paper.

3. Fast calculation of propeller vibration and flow mesh deformation

In this paper, the fast dynamic mesh method reported in literature [6] is applied in the research of the fluid structure interaction of propellers. The decoupled dynamic equations in modal coordinates of the propeller-pseudo elastic solid system can be derived through modal analysis and coordinate transformation.

4. Efficient fluid structure coupling algorithm

Fluid structure coupled computations of propellers consist of flow analysis, vibration analysis of the propeller and calculation of the flow mesh deformation. Both the inner iterations for the flow analysis and iterations between the flow and the propeller vibration are needed in the existing fluid structure coupling algorithms. So, the existing coupling algorithms are computationally expensive. An efficient coupling algorithm has been developed based on a fast dynamic mesh method in this paper to reduce the computing time of coupling algorithms furthermore for propellers through iterative computations called single-loop iterations between flow, propeller and the flow dynamic mesh. The efficient fluid structure coupling algorithm of this paper is sketched in Fig. 1.

5. Fluid structure coupled computations for a propeller

One blade of a propeller is modeled in this paper. The finite elements for the propeller blade are shown in Fig. 2(a). The number of the nodes is 8487 and the number of the elements is 6120. There are 6052 8-node hexahedral elements and 68 6-node prism elements. The density of the propeller blade is 7400 Kg/m³, the elasticity modulus is 1.22E11 Pa and the Poisson’s ratio is 0.25. The rotational speed of the propeller is 80 r/min. The flow mesh for single one propeller blade is shown in Fig. 2(b). The flow mesh is divided into 2 parts: the green mesh around the blade is the dynamic mesh zone where the rotating coordinate system is employed to simulate the rotation of the propeller and the other part is the stationary flow mesh zone where the stationary coordinate system is employed. The 2 sides in the circumferential direction are cycle-symmetry and there is a one-to-one correspondence between the flow mesh nodes on the 2 sides for both the dynamic mesh zone and the stationary mesh zone. Elements for the flow mesh are 8-node hexahedral elements of which the total number is 506042 and the total number of the nodes is 536237. The number of elements of the dynamic mesh is 328480 and the number of the nodes is 342702. The flow dynamic mesh is shown in Fig. 3(a) and the flow mesh on the cross section of the propeller blade is shown in Fig. 3(b).

Fig. 1Efficient fluid structure coupling algorithm for propellers

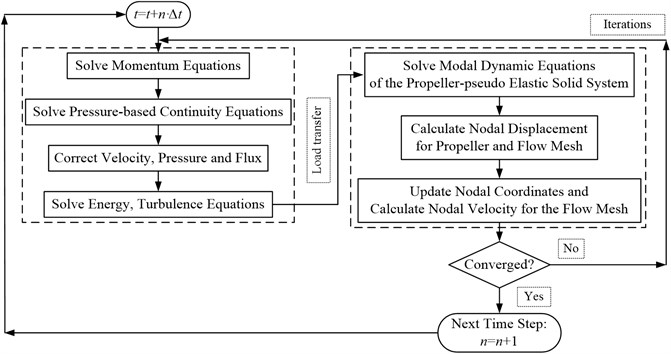
Fig. 2Mesh of the propeller and flow

a) Finite elements of the propeller blade

b) Flow mesh for one single propeller blade

Fig. 3Flow dynamic mesh of the propeller blade

a) Flow dynamic mesh

b) Flow mesh on the cross section

The calculated flow pressure on the cross section at the middle span with different meshes is shown in Fig. 4. The dimensionless length is the ratio of the distance between the point located on the curve of the cross section and the stagnation point at the leading edge of the section to the length of the curve. The attack angle of the section is positive.

As shown in Figure.4, the flow pressure on the cross section at the middle span verges to a constant value with the quantity of the flow mesh increases. The calculated flow pressure remains unchanged while the computational complex increases with the increase of the quantity of the flow mesh when the quantity of the flow mesh exceeds 506042. Thus, 506042 is an appropriate value for the quantity of the flow mesh. The flow mesh of which the quantity is 506042 was employed for computations in this paper. The calculated Y+ on the cross section at the middle span is shown in Fig. 5. It can be seen that the calculated Y+ which is greater than 35 and less than 65 meets the “Y+>30” requirement of the RNG $k$-$\epsilon$ turbulence model. Therefore, the calculated results of the flow are credible in this paper.

Fig. 4Flow pressure on the cross section at the middle span

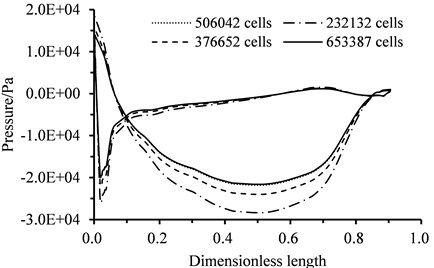
Fig. 5Calculated Y+ on the cross section at the middle span

The flow induced vibration of the propeller blade was computed using the present fluid structure coupling algorithm in this paper with the calculated results of the steady flow as the initial value. The curves of the relative residuals of the flow variables versus iterations for 1 time step are shown in Fig. 6(a). The $x$ direction is tangent to the circular direction of the propeller blade. The y direction is mainly in common with the radial direction of the propeller blade. The $z$ direction is where the rotation shaft locates. The relative residuals of the flow variables descend to a certain small value and stay unchanged after 23 iterations. The relative residual of the continuity descends to 5.32E-05. The relative residual of the $x$-velocity descends to 7.52E-04. The relative residual of the $y$-velocity descends to 9.03E-07. The relative residual of the $z$-velocity descends to 3.47E-08. The relative residual of the turbulent energy $k$ descends to 4.90E-09. The relative residual of the turbulent energy dissipation rating $\epsilon$ descends to 7.37E-09. It can be concluded that the computation is convergent. The number of the fluid structure coupling iterations between the flow and the propeller-pseudo elastic solid system is 16 and the number of the inner iterations for the flow is 193 using an existing fluid structure coupling algorithm for the convergent computations of the propeller blade. The residuals curves of the existing fluid structure coupling algorithm are shown in Fig. 6(b). A 4 cores CPU of which the main frequency is 3.2 GHz is employed in this paper and the maximum memory can be called is 16G. The computing time of 1 time step using the present coupling algorithm is 26.5 s while the computing time of 1 time step using the existing fluid structure coupling algorithm is 228.3 s. Obviously, the computing time is reduced by 88.4 % through the efficient fluid structure coupling algorithm of this paper compared with the existing fluid structure coupling algorithm.

Fig. 6Residuals of the flow variables vs. iterations

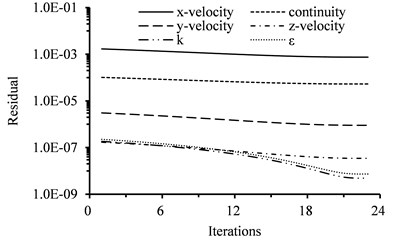
a) Present fluid structure coupling method

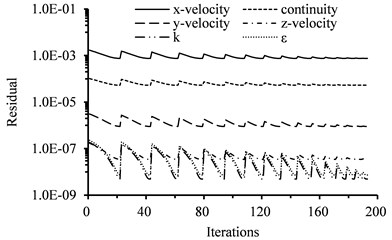
b) Existing fluid structure coupling method

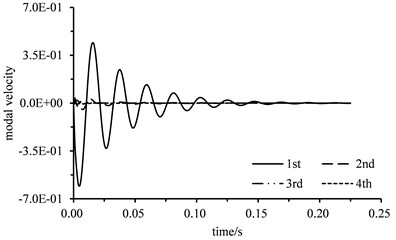
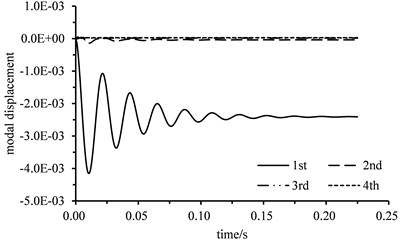
The curves of calculated displacement and velocity of the 1st four modes versus time through fluid structure coupled computations are shown in Fig. 7. The modal displacement of the 1st mode is 20 times the modal displacement of the 2nd mode. It can be seen that the vibration of the rotating propeller blade is excited by its hydrodynamic force and the vibration of the 1st mode is the dominant. The vibration of the blade attenuates versus time and the blade finally stabilizes at the equilibrium position. Namely, the propeller blade will produce a certain deformation to balance the hydrodynamic force in the actual operation.

Fig. 7Results of fluid structure coupled calculation for the propeller blade

a) Modal displacement

b) Modal velocity

6. Conclusions

An efficient coupling algorithm of fluid structure interaction for propeller flow has been proposed and applied to calculate the fluid structure coupled vibration of a propeller blade in this paper. The mesh independence verification is performed for the flow mesh. The computing time is reduced by 88.4 % using the present algorithm in this paper compared with the existing fluid structure coupling method. Results show that the vibration of the rotating blade is excited by its hydrodynamic force and the vibration of the 1st mode is the dominant. The vibration of the blade attenuates versus time and the blade finally stabilizes at the equilibrium position.